geometry24

ЛЕКЦИЯ1.НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ АЛГЕБРЫ

§1.Определители второго порядка

Рассмотрим систему двух линейных уравнений относительно двух неизвестных

x и y:
	a1x + b1y = c1
	a2x + b2y = c2	(1.1)

Здесь a1, b1, a2, b2 коэффициенты при неизвестных, c1 и c2 свободные члены. Умножим первое уравнение системы на b2 ,а второе на b1 ,затем вычтем из

первого полученного уравнения второе:

(a1b2 − a2b1)x = b2c1	− b1c2.	(1.2)
Аналогично,домножая первое уравнение на a2 ,а второе на		a1 и вычитая из
второго полученного уравнения первое,найдем
(a1b2 − a2b1)y = a1c2	− a2c1.	(1.3)

Как видим,в обоих уравнениях перед неизвестными x и y получился один и тот же множитель a1b2 − a2b1 .

Определение. Определителем второго порядка называется число,равное a1b2 −a2b1

	"	a1	b1	"			a1	b1
и обозначаемое	"	a2	b2	"	или det		a2	b2	.
	"			"
Числа a1, a2", b1, b2 называют"						элементами определителя,индекс показывает номер

строки,а алфавитный порядок буквы номер столбца,в котором стоит данный элемент.Элементы a1 и b2 образуют главную диагональ определителя,а элементы

a2 и b1 побочную.

Из определения определителя сразу же следует,что

"

"" a1 " b1

a2

"

"

a1

b1

"

"

b1

a1

"

b2

"

=

"

a2

b2

"

,

"

b2

a2

"

=

"

"

"

"

"

"

"

"

"

"

""

−""" a1 a2 """ , b1 b2

т.е.определитель не изменяется при замене его строк на столбцы и меняет знак при перестановке столбцов.

Очевидно,решение системы уравнений(1.1)при a1b2 6= a2b1 можно записать через определители в виде( формул Крамера)

"		c2	b2	"	"		a2	c2	"
x = "		c1	b1	"	, y = "		a1	c1	".
"		a1	b1	"	"		a1	b1	"
"		a2	b2	"	"		a2	b2	"
"				"	"				"
	"			"		"			"
"				"	"				"
"				"	"				"

Определитель,стоящий в знаменателе,составлен из коэффициентов системы линейных уравнений(1.1)и называется определителем этой системы,определители в числителях получаются из этого определителя заменой его первого и второго столбцов соответственно на свободные члены.

1

Заметим,что определитель	"	a1	b1		"	равен нулю тогда и только тогда,когда
	"	a2	b2		"
его строки или столбцы соответственно"				пропорциональны"			.Это следует из того,что
каждая из пропорций a1/a2 = b1/b" 2 и a1/b"						1 = a2/b2 эквивалентна равенству a1b2 =
= b1a2 1.

Если определитель системы равен нулю,а среди числителей есть хотя бы один ненулевой,то система уравнений(1.1) несовместна,т.е.не имеет решений

(см. (1.2),(1.3)).

Рассмотрим случай

"

a1

b1

"

"

c1

b1

"

"

a1

c1

"

"

a2

b2

"

=

"

c2

b2

"

=

"

a2

c2

"

= 0.

"

"

"

"

"

"

"

"

"

"

"

"

При этом условии система(1.1)имеет бесконечно много решений(такая система называется неопределенной),так как соответствующие коэффициенты уравнений, очевидно,пропорциональны и система сводится к одному уравнению от двух переменных.

Пример1.1. Решить систему уравнений

a1x + b1y + c1z = 0 a2x + b2y + c2z = 0

Решение. Пусть среди определителей

"

a1

b1

"

"

a1

c1

"

"

b1

c1

"

"

a2

b2

"

,

"

a2

c2

"

,

"

b2

c2

"

"

"

"

"

"

"

"

"

"

"

"

"

хотя бы один(пусть первый)отличен от нуля.Тогда перенесем все слагаемые с правую часть и найдем x и y по формулам Крамера:

x =

"

c1

b1

"

, y =

"

a1

c1

"

,

−

"

a1

b1

"

−

"

a1

b1

"

"

c2

b2

" z

"

a2

c2

" z

"

a2

b2

"

"

a2

b2

"

"

"

"

"

"

"

"

"

"

"

"

"

"

"

"

"

(1.4)

z в

где z произвольно,и система имеет бесконечное множество решений.

Если же все три определителя(1.4)нулевые,то соответствующие коэффициенты всех уравнений будут пропорциональны,и система сведется к одному уравнению

a1x + b1y + c1z = 0,

откуда при a1 6= 0,например,получим

x = −b1y + c1z , a1

а y и z могут принимать произвольные значения.

1Пропорциональность a1/a2 = b1/b2 здесь понимается в том смысле,что существует число k , такое,что a1 = ka2, b1 = kb2 ,так что числа a1, a2, b1, b2 могут быть равны нулю.В старых английских книгах пропорция записывалась следующим образом: a1 : a2 :: b1 : b2 ,без знака равенства, выражая именно пропорциональность числовых пар.

2

§2.Определители третьего порядка
Определение. Определителем третьего порядка называется число
"	a3	b3	c3	"			−		−	−
"	a1	b1	c1	"
"	a2	b2	c2	"	= a1b2c3 + a2b3c1	+ a3b1c2		a3b2c1	a1b3c2	a2b1c3.	(2.1)
"				"
"				"
"				"

Два простых правила запоминания этого выражения.

I. Выпишем все элементы определителя третьего порядка и припишем справа к ним первые два столбца.На рис. 1показано,произведения каких элементов берутся со знаком“плюс”,а каких со знаком“минус”.

II. Обозначим точками элементы определителя.На рис. 2показано,произведения каких элементов берутся со знаком“плюс”,а каких со знаком“минус”.

Пример2.2.

2 "

· ·

· ·

− ·

·

− · ·

− · · − − · ·

"

−2

5

"

1

2

3

"

"

1

3

4

"

= 1 3 2 + 2 4 2 + ( 1) 5 3 3 3 2 4 5 1 ( 1) 2 2 =

"

"

"

"

"

"

= 6 + 16

−

15

−

18

−

20 + 4 =

−

27.

§3.Основные свойства определителей

I. При замене строк столбцами величина определителя не меняется(равноправность строк и столбцов).

"	a1	b1	c1	"		"	a1	a2	a3	"
"	a2	b2	c2	"	=	"	b1	b2	b3	"
"				"		"				" .
"				"		"				"
"	a3	b3	c3	"		"	c1	c2	c3	"
"				"		"				"

Доказательство. Справедливость этого свойства сразу вытекает из правилаI.

3

II. При перестановке двух столбцов(строк)определитель меняет знак.Например,для перестановки второго и третьего столбцов имеем

"	a1	c1	b1	"		"	a1	b1	c1	"
"	a2	c2	b2	"	=	"	a2	b2	c2	"
"				"		"				" .
"				"		"				"
"	a3	c3	b3	"		"	a3	b3	c3	"
"				"		−"				"

Доказательство. И это свойство легко следует из правилаI,так как меняются местами элементы,входящие в произведения,которые берутся со знаком“плюс”и элементы,входящие в произведения,которые берутся со знаком“минус”,что равносильно смене знака определителя.

III. Если в определителе два одинаковых столбца(две одинаковые строки),то он равен нулю.

Доказательство. Действительно,если меняем местами два одинаковых столбца, то,с одной стороны,определитель не меняется,а с другой стороны,по свойствуII, он меняет знак.

Перед формулировкой следующих свойств нам понадобятся некоторые новые понятия.

Рассмотрим определитель

	"	a1	b1		c1	"
=	"	a2	b2		c2	"
	"					" .
	"					"
	"	a3	b3		c3	"
Определение. Минором данного элемента"				определителя"			называется определи-

тель2-го порядка,который получается из данного определителя вычеркиванием

строки и столбца,на пересечении которых стоит данный элемент.

"

b2

c2

"

b1

c1

a1

равен

"

b3

c3

"

,минор элемента a2

равен

"

b3

Например,минор элемента

"

"

c3

"

и т.д.

"

"

"

"

"

"

"

"

Определение. Алгебраическим дополнением A некоторого элемента a называется соответствующий минор,взятый со знаком“плюс”,если сумма номеров строки и столбца,которым принадлежит данный элемент,четна,и“минус” в противном случае.

Так,например,алгебраическим дополнением элемента b3 будет2

		"	a1	c1	"
B3	= −	"	a2	c2	"
		"			" .
		"			"

Следующая таблица дает наглядное представление,каким знаком связаны алгебраическое дополнение и соответствующий минор:

"	− +		−	" .
"	+	−	+	"
"	+		+	"
"		−		"
"				"
"				"

2Большими буквами с соответствующими индексами будем обозначать алгебраические дополнения элементов,обозначенных маленькими буквами.

4

IV. Сумма произведений элементов некоторого ряда(строки или столбца)на алгебраические дополнения этих элементов равна определителю.Сумма произведений элементов некоторого столбца(строки)на алгебраические дополнения элементов другого столбца(строки)равна нулю.

Доказательство. Раскладывая сумму,которая стоит в правой части формулы(2.1) по элементам,например,первого столбца,получим

= a1(b2c3 − c2b3) + a2(c1b3 − b1c3) + a3(b1c2 − c1b2) = a1A1 + a2A2 + a3A3. (3.1)

Аналогичное разложение можно получить и для элементов любого другого ряда (строки или столбца).

А теперь разложим по первому столбцу нулевой определитель(определитель с

двумя одинаковыми столбцами):
"	b1	b1	c1	"
"	b2	b2	c2	"	+ b2A2	+ b3A3.
0 = "				" = b1A1
"	b3	b3	c3	"
"				"
Аналогичным образом"получается				"формула

c1A1 + c2A2 + c3A3 = 0.

Тем самым,для первого столбца свойство IV доказано. Разумеется,аналогичные свойства выполняются для любых рядов.

V. Множитель,общий элементам некоторого ряда,можно выносить за знак определителя.

VI. Если в определителе есть нулевой ряд,то он равен нулю. Доказательство. Свойства V и VI следуют из разложения определителя по указанному ряду.

VII. Если элементы некоторого ряда равны сумме двух слагаемых,то определитель равен сумме двух определителей,у которых элементы рассматриваемого ряда равны соответствующим слагаемым.

Это свойство очевидным образом распространяется на любое количество слагаемых.

Доказательство. Для доказательства предположим,например,что

a1 = a01 + a001, a2 = a02 + a002, a3 = a03 + a003.

Разложим по первому столбцу,получим

= (a01 + a001)A1 + (a02 + a002)A2 + (a03 + a003)A3 =

(a01A1 + a02A2 + a03A3) + (a001A1 + a002A2 + a003A3) = 0 + 00.

Здесь 0 получается из заменой в нем первого столбца на a01, a02, a03 , а 00 на

a001, a002, a003 .

VIII. Значение определителя не изменится,если к элементам какого-либо его ряда прибавить элементы параллельного ряда,умноженные на одно и то же произвольное число.

Доказательство. Заменим,например,элементы первой строки на a1 + la2, b1+ +lb2, c1 + lc2 .По предыдущему свойству,определитель представ´им в виде суммы двух определителей,первый из которых ,а второй после вынесения из первой строки общего множителя всех ее элементов l будет иметь две одинаковые строки первую и вторую,то есть равен нулю.

5

Пример3.3. Вычислить определитель

	"	4	7	6	"
	"	2	3	4	"
=	"	1	2	5	"
	"				" .
	"				"
	"				"

Решение. Из второго столбца вычтем первый,умноженный на2,а из третьегопервый,умноженный на5,далее раскладываем определитель по первому столбцу:

"

4

1

14

"

−"

−1

14

"

−

"

"

1

6

"

2

−1

−6

"

"

−

"

−

−

−

=

"

1

0

"

=

"

−

"

=

8.

"

"

"

"

"

"

§4.Система трех линейных уравнений с тремя неизвестными с определителем,отличным от нуля

						a1x + b1y + c1z = d1
						8 a2x + b2y + c2z = d2			(4.1)
						< a3x + b3y + c3z = d3
		"	a1	b1	c1:
						"	y z
Определитель	=	"	a2	b2	c2	"
		"				" называется определителем системы.
		"	a3	b3	c3	"	и	умножим уравнения(4.1)соответственно на
Для исключения"			неизвестных"
алгебраические дополнения"					A1,"A2		и A3	элементов первого столбца определителя

системы и после этого сложим все уравнения,получим

(A1a1 + A2a2 + A3a3)x + (A1b1 + A2b2 + A3b3)y + (A1c1 + A2c2 + A3c3)z =

= A1d1 + A2d2 + A3d3.

По свойству IV имеем

A1a1 + A2a2

A1d1 + A2d2

откуда

и

+ A3a3 = , A1b1 + A2b2

		"	d1	b1	c1	"
+ A3d3	=	"	d2	b2	c2	"	=
		"				"
		"				"
		"	d3	b3	c3	"
		"				"
					x		=

+A3b3 = 0, A1c1 + A2c2 + A3c3 = 0,

x,

x

(4.2)

	x =		x	.
Аналогично получаем
y =	y	,	z =		z	,

где		a1	d1	c1
	"				"
y =	"	a2	d2	c2	"	,
	"				"
	"				"
	"	a3	d3	c3	"
	"				"

"

"" a1

z = "" a2 " a3

"

b1 d1 "" b2 d2 "" , b3 d3 "

6

то есть определители x, y и z получаются из заменой свободными членами элементов соответственно первого,второго и третьего столбцов.Приведенные фор-

мулы называются формулами Крамера.

Поскольку уравнение(4.2)является,как и аналогичные уравнения для y и z, следствием исходной системы,то формулы Крамера доказывают единственность ее

решения.

Убедиться,что полученные по формулам Крамера значения действительно дают решение системы(4.1),достаточно легко,нужно просто подставить их в каждое уравнение и получить верное равенство.Сделаем это для первого уравнения:

a1x + b1y + c1z = a1

x

+ b1

y

+ c1

z

=

=

1

[a1(d1A1 + d2A2 + d3A3) + b1(d1B1 + d2B2 + d3B3)+

+c

(d

C

+ d

C

+ d

C

) =

1

[d (a

A

+ b

B

+ c C1)+

1

1

1

2

2

3

3

1 1

1

1

1

1

IV 1

+d2(a1A2 + b1B2 + c1C2) + d3(a1A3 + b1B3 + c1C3)

=

(d1

) = d1.

Таким образом,если определитель системы отличен от нуля,то существует единственное решение системы,которое находится по формулам Крамера.

§5.Понятие определителя любого порядка

В общей задаче решения и исследования систем уравнений первой степени со многими неизвестными и во многих других вычислительных задачах математики приходится иметь дело с определителями n-го порядка n = 2, 3, 4, . . . Теория определителей произвольного порядка строится в общих чертах аналогично теории определителей второго и третьего порядков.Эта теория,как и теория систем уравнений первой степени со многими неизвестными,излагается в курсе высшей алгебры.Ограничимся здесь лишь следующими сведениями:

1.Определитель порядка n задается квадратной таблицей чисел(элементов определителя),имеющей n строк и n столбцов.Обозначается определитель порядка n аналогично определителям порядков2и3.

2.Минором некоторого элемента определителя порядка n называется определитель порядка n − 1,получаемый из данного вычеркиванием строки и столбца,на пересечении которых расположен этот элемент.

3.Алгебраическое дополнение некоторого элемента определителя есть минор этого элемента,взятый со знаком (−1)i+j ,где i номер строки,а j номер столбца, на пересечении которых стоит данный элемент.

4.Определитель равен сумме произведений элементов какого-либо столбца(или строки)на их алгебраические дополнения.Тем самым,вычисление определителя порядка n сводится к вычислению n определителей порядка n − 1.

5.Все изложенные выше свойства определителей относятся к определителям любого порядка.

Пример5.4. Вычислить определитель

	"	3	2	8	5	"
	"	2	4	4	6	"
=	"	2	8	7	3	"
	"	4	2	5	5	" .
	"					"
	"					"
	"					"
	"					"

7

Решение.Раскладывая этот определитель по элементам первой строки,то есть представляя его в виде суммы произведений элементов первой строки на их алгебраические дополнения,находим

"

8 7 3 "

−

"

2 7 3 "

"

2 8 3 "

−

"

2 8 7 "

"

2

5

5

"

"

4

5

5

"

"

4

2

5

"

"

4

2

5

"

= 2

"

2 8 5

"

4

"

3 8 5

"

"

3 2 5

"

6

"

3 2 8

"

=

"

"

"

"

+ 4 "

"

"

"

"

"

"

"

"

"

"

"

="

2

·

−

102)"

−

4

·

−

14) + 4"

·

(

−

−

6

·

−

110)"

= 376.

"

(

"

(

"34)

("

Замечание. Вычисление определителя можно упростить,если воспользоваться

свойством VIII.

В самом деле,вычтем из второй строки первую,умноженную на

2,а из послед-

ней первую:

"

3

−2

−8

−5

"

"

2

4

4

6

"

0

4

3

3

"

"

,

= "

0

6

3

7

"

"

−

"

"

"

"

"

"

"

в полученном определителе из первой строки вынесем множитель 2,после чего получившуюся первую строку,домноженную на 3,вычтем из третьей строки и разложим определитель по первому столбцу:

"

0

−4

−2

−4

"

"

"

"

1

2

2

3

"

"

6

3

7

"

0

−4

3

−3

−4

3

−3

= 2

"

"

= 2

"

−4

−2

"

.

"

0

6

3

7

"

"

−4

"

−

"

−

"

"

"

"

"

"

"

"

"

"

"

Далее вычисляем определитель третьего порядка:

"

−4

3

−3 "

"

10

0

3 "

·

"

6

3

7

"

"

−2

0

−10

"

= 4

"

−2

−1

−

"

= 4

"

−2

1

−2

"

= 4 94 = 376.

"

−2

"

"

"

"

"

"

"

"

"

"

"

8

ЛЕКЦИЯ2.ВЕКТОРЫ В ПРОСТРАНСТВЕ

§6.Векторы и линейные операции над ними

Определение. Прямая с выбранным на ней положительным направлением называется осью.

Обычно ось изображается прямой с отмеченным стрелкой положительным направлени-

ем(рис. 1).

Определение. Вектором называется направленный отрезок прямой,т.е.упорядоченная пара точек.

Одна из двух конечных точек вектора называется его началом,вторая концом.Вектор направлен от начала к концу.Направление вектора

указывается стрелкой(рис. 2).

Обозначать вектор с началом в точке A и концом в точке B будем AB либо одной латинской буквой a.Вектор AA называется нулевым вектором и обозначается 0A .Направление

нулевого вектора не определено.

Определение. Длиной вектора называется расстояние между его концами

|AB| = %(A, B).

В частности,длина вектора равна нулю тогда и только тогда,когда вектор нулевой.

Определение. Векторы называются коллинеарными,если существует прямая,которой они параллельны.

Нулевой вектор считается параллельным,а следовательно,и коллинеарным любой прямой.

Определение. Векторы называются компланарными,если существует плоскость, которой они параллельны.

В большинстве задач,которые мы будем рассматривать,важны только длина вектора и его направление.

Определение. Векторы равны,если они коллинеарны,одинаково направлены и имеют равные длины.

В некоторых задачах математики,механики и физики используются также векторы,отличные от рассмотренных нами свободных векторов,т.е.тех векторов,для которых положение начала несущественно.Несвободные векторы бывают скользящими (равные векторы,лежащие на одной прямой)и связанными (равные векторы с началом в одной точке).

Из определения равенства векторов следует,что для любых вектора a и точки

Mсуществует единственный вектор MN с началом в точке M ,равный вектору a.

Всамом деле,через точку M проходит одна и только одна прямая,параллельная прямой,на которой лежит вектор a.На этой прямой существует единственная точка

Nтакая,что |MN| = |a| и вектор MN сонаправлен вектору a.

Пусть даны вектор AB и ось u.Обозначим через A0 и B0 основания перпендикуляров,опущенных из точек A и B на u соответственно.

9

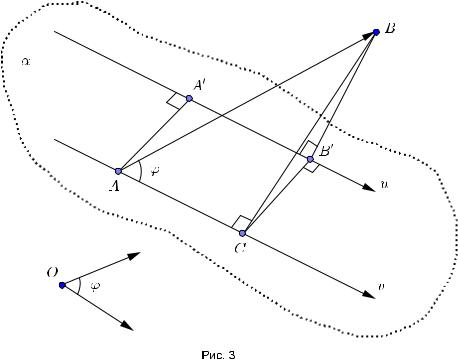
Определение. Проекцией вектора AB на ось u называется длина отрезка A0B0 , взятая со знаком плюс,если вектор A0B0 сонаправлен оси u,и со знаком минус, если этот вектор и ось u имеют противоположные направления.

Определение. Углом наклона вектора AB к оси u называется угол ' между двумя выходящими из произвольной точки M лучами,направление одного из которых совпадает с направлением вектора AB,а направление второго совпадает с направлением оси u.

Теорема6.1. Проекция вектора a = AB на ось u равна произведению длины этого вектора на косинус угла наклона вектора a к оси.

Доказательство. Проведем через точку A ось v,имеющую то же направление, что и u.Обозначим через плоскость,в которой лежат оси u и v.Пусть C проекция точки B на ось v.По теореме о трех перпендикулярах проекцией точки C на ось u является точка B0 (рис. 3).Четырехугольник AA0B0C прямоугольник, тем самым AC = A0B0 .Оси u и v имеют одно и то же направление,следовательно, нам нужно найти проекцию вектора AB на ось v.Из прямоугольного треугольника ABC получаем,что абсолютное значение проекции равно |AB|| cos '|.Если угол ' острый,то проекция будет положительна,а если тупой отрицательна.Таким образом,теорема доказана.

Определение. Линейные операции над векторами: 1) Сложение по правилу треугольника(рис. 4).

Суммой векторов a и b при условии,что начало вектора b совпадает с концом вектора a называется вектор,идущий из начала вектора a в конец вектора b.

2) Умножение вектора на вещественное число b = a по правилу:

1)b коллинеарен a;

2)|b| = | ||a|;

3) b сонаправлен с a,если > 0,и противоположно направлен,если < 0.

10