UMF-BOOK

Глава 1

Вводные понятия дифференциальных уравнений в частных производных и краевых задач

§ 1. Понятие дифференциального уравнения в частных производных

Рассмотрим область D Rn, где Rn n–мерное евклидово простаранство, n ≥ 2.

Пусть точка x D и

x1, x2, . . . , xn ee декартовые прямоугольные координаты, x =

(x1, . . . , xn). Пусть F (x, . . . , pi1...in , . . . ) – заданная вещественная

функция точек x

D и

n

вещественных переменных pi1...in , где ij – целые, неотрицательные,

Pj=1

ij = k, k = 0, m,

m ≥ 1 и по крайней мере одна из частных производных

n

∂F

X

∂pi1...in

6= 0,

ij = m.

j=1

Определение 1.

Равенство вида

∂ku

(1.1)

F x, . . . ,

, . . . = 0,

∂x1i1 . . . ∂xnin

называется дифференциальным уравнением в частных производных порядка m относительно непрерывной функции u(x), u(x1, x2, . . . , xn), а левая его часть – диф-

ференциальным оператором или дифференциальным выражением в частных производных порядка m.

Определение 2. Вещественная функция u(x), определенная в D, непрерывная вместе со своими частными производными порядка m (u C(m)(D)) и обращающая (1.1)

в верное тождество, называется регулярным решением.

Определение 3. Решение, теряющее свойство регулярности в изолированных точках, линиях, поверхностях или многообразиях особого рода называется элементарным, или фундаментальным.

1

М.А. Греков Уравнения математической физики

Дифференциальные уравнения, отражающие реальные физические процессы, как правило имеют множество решений. В некоторых случаях множества решений весьма

узки или даже пусты. В частности,

n

∂u

2

i=1

∂xi

= 0 u(x) = const

X

n

∂u

2

i=1

∂xi

+ 1 = 0 вещественных решений нет.

X

Определение 4.

Дифференциальное уравнение (1.1) линейно, если функция F

– линейная функция относительно всех переменных p

,

n

i

i1

...in

= k, k = 0, m. Если

j=1

j

n

функция

F

линейна только относительно старших производных p

i1...in

,

i

j =

m,

P

P

j=1

то (1.1) – квазилинейное уравнение.

Линейное уравнение будем обозначать

L u = f,

(1.2)

где L – линейный дифференциальный оператор. Если f ≡ 0, x D, то (1.2) – однородное, а если f 6≡0, то (1.2) – неоднородное.

Если u(x), v(x) – решения неоднородного уравнения (1.2), то w = u − v – решение

уравнения Lw = 0. Кроме того, если uk – решение уравнения L uk							= 0, k = 1, l,
	P
то u =	l						– вещественные
	k=1 Ckuk(x) будет удовлетворять уравнению L u = 0, где Ck
постоянные.
Рассмотрим линейное дифференциальное уравнение в частных производных вто-
рого порядка. Его общий вид:
	n			n
	X	∂2u		X	∂u		(1.3)
	Ajk(x)		+	Bj(x)		+ C(x)u = f(x),
		∂xj ∂xk			∂xj
	j,k=1			j=1

где Ajk, Bj , C, f - заданные в D вещественные функции точки x. Причем, не существует

такой точки x, в которой все Ajk = 0, иначе (1.3) выродилось бы в этой точке в диффе-

P

ренциальное уравнение в частных производных первого порядка. В дальнейшем знак часто будем опускать, считая, что по повторяющимся греческим индексам производится суммирование. Так, вместо (1.3) будем писать:

Aαβ (x)

∂2u

+ Bα(x)

∂u

+ C(x)u = f(x).

∂xα∂xβ

∂xα

В уравнении (1.3) можно считать, что Akj = Ajk,

j 6= k, т.к.

∂2u

∂2u

∂2u

1

∂2u

∂2u

.

=

=

+

∂xj ∂xk

∂xk∂xj

∂xj ∂xk

2

∂xj ∂xk

∂xk∂xj

2

М.А. Греков

Уравнения математической физики

Действительно, пусть Akj 6= Ajk. Тогда

.

∂2u

∂2u

A + A

kj

∂2u

∂2u

Ajk

+ Akj

=

jk

+

∂xj ∂xk

∂xj ∂xk

2

∂xj ∂xk

∂xk∂xj

Следовательно, матрица коэффициентов при вторых производных симметрична.

§ 2. Вывод простейших дифференциальных уравнений.

2.1Уравнение колебаний

Во многих случаях колебательный процесс описывается уравнением

ρ	∂2u	− r · (pru)) + qu = f(x, t),	(2.1)
	∂t2

где p = p(x), q = q(x), ρ = ρ(x) определяются свойствами среды, где происходит колебательный процесс, f(x, t) интенсивность внешнего возмущения, u = u(x, t) отклоне-

ние точки от положения равновесия. Согласно определению,

		r · (pru) ≡ div(p grad u) = i=1 ∂xi		p∂xi ,
		n
		X	∂		∂u
	∂
где r =		eα, eα орт оси xα.
	∂xα

Малые поперечные колебания струны. Определение 1. Струна упругая нить, не сопротивляющаяся изгибу.

Рис. 1.1.

Малые колебания струны характеризуются условием

| tg α| =		∂x		1,	(2.2)
		∂u

3

М.А. Греков Уравнения математической физики

где u = u(x, t) уравнение положения струны в момент t.

Из определения следует, что натяжение струны T (x, t) в точке x направлено по касательной к струне. Кроме того, любой участок струны (a, b) при отклонении от пря-

молинейного положения равновесия практически сохраняет свою длину:
l =	ab s1 +		∂u	2dx ≈ b − a = l0.		(2.3)
	Z

∂x

В момент времени t натяжение струны T можно представить в виде

T = T0 + T1,

где T0 натяжение струны при t = 0, а T1 дополнительное усилие в результате

отклонения струны от положения равновесия.

По закону Гука		l
T1 = E			,	l = l − l0.
		l0
Полагая, что | l/l0| T0/E, получаем

|T (x, t)| ≈ const = T0.

Пусть F (x, t) плотность внешних сил в точке x в момент t, направленных перпендикулярно оси x, ρ(x) линейная плотность в точке x, т.е. ρdx масса элемента dx.

Согласно закону Ньютона, проектируя все силы на вертикальную ось, получим

∂2u

T0 sin α|x+dx − T0 sin α|x + F (x, t)dx = ρ(x)dx

.

∂t2

Так как

∂u

sin α α tg α =

,

то

∂x

∂2u

1

∂u(x + dx)

∂u(x, t)

ρ

− T0

−

= F (x, t).

∂t2

dx

∂x

∂x

При dx → 0 приходим к уравнению вынужденных малых поперечных колебаний

струны
ρ		∂2u			− T0		∂2u		= F (x, t)		(2.4)
		∂t2					∂x2
При ρ(x) = const, уравнение записывается в виде
	∂2u				2 ∂2u						(2.5)
					− a				= f(x, t)
	∂t2					∂x2
и называется одномерным волновым уравнением.
Здесь a2 = T0/ρ, f(x, t) = F (x, t)/ρ,										.
{Aij} = 0 −a2
					1				0

4

М.А. Греков Уравнения математической физики

Уравнение (2.5) при f = 0 уравнение свободных колебаний струны.

Двумерным аналогом уравнения (2.5) является уравнение малых колебаний

мемраны								= f(x, y, t),
	∂2u		− a2		∂2u	+	∂2u				(2.6)
	∂t2				∂x2		∂y2
			Aij	= 0			−a2		0	.
						1	0		0
		{ }				0	0		−a2

Уравнение колебания струны в среде с сопротивлением имеет вид

∂2u		− a	2 ∂2u			+ h	∂u	= f(x, t), h = const.
∂t2				∂x2			∂t

Продольные колебания упругого стержня описываются уравнением

ρS	∂2u		−	∂	ES	∂u	= SF (x, t),
	∂t2			∂x		∂x

где S площадь поперечного сечения, ρ объмная плотность, E – модуль Юнга,

сила на единицу объема.

(2.7)

(2.8)

F (x, t)

Замечание 1. В отличие от струны, которая не сопротивляется изгибу, уравнение малых поперечных колебаний упругого стержня в упрощенном варианте является уравнением четвертого порядка

∂2u + c2 ∂4u = f(x, t) ∂t2 ∂x4

и справедливо для малых частот колебаний c.

Трехмерное волновое уравнение
∂2u	− a2 u = f	(2.9)
∂t2

описывает процессы распространения звука в однородной среде и электромагнитных волн в однородной, непроводящей среде. Этому уравнению удовлетворяет плотность газа, его давление и потенциал скоростей, а также составляющие напряженности электрического и магнитного полей и соответствующие потенциалы.

Волновой оператор обычно обозначают

	∂2			∂2		∂2
a =		− a2 ,	=		+ · · · +		.
	∂t2			∂x12		∂xn2

Здесь – оператор Лапласа. При a = 1 принято 1 ≡ .

Уравнение движения однородной изотропной упругой среды:
		∂u2		(2.10)
pr(r · u) + q	u + ρF = ρ		.
		∂t2

5

М.А. Греков	Уравнения математической физики

Здесь p, q постоянные величины, ρ плотность, F(x1x2x3) сила на единицу массы. При F = 0 уравнение (2.10) распадается на три уравнения

Если вектор перемещений u = u(x1, t), то говорят о плоских волнах, распространяющихся параллельно оси x1.

2	∂u2		∂u2		2	∂u2		∂u2		2	∂u2		∂u2
	1		1			2		2			3		3		(2.11)
cL		=		,	cT		=		,	cT		=		.
	∂x2		∂t2			∂x2		∂t2			∂x2		∂t2
	1					1					1

Решения этих уравнений представимы в виде

uj = fj (x1 − ct) + gj(x1 + ct), c = cL, cT , j = 1, 2, 3.

2.2 Уравнение диффузии и распространения тепла (уравнение теплопроводности)

Явление диффузии и распространение тепла описываются одним и тем же уравнением

ρ	∂2u	− div(p grad u) + qu = F (x, t).	(2.12)
	∂t2

Различие состоит лишь в физической сути входящих в уравнение параметров. Выведем уравнение распространения тепла. В (2.12) u(x, t) температура сре-

ды в точке x = (x1, x2, x3), ρ(x) плотность, c(x) удельная теплоемкость, k(x) коэффициент теплопроводности. Будем считать, что среда изотропна. Пусть F (x, t) интенсивность источников тепла в точке x в момент времени t, то есть количество тепла,

поглощаемого или выделяемого в единицу времени в единице объема.

Подсчитаем баланс тепла в произвольном объеме V с границей S за время dt.

Закон Фурье. В направлении вектора нормали n к поверхности S поток тепла в единицу времени через элемент dS равен:

	∂u	(2.13)
dQ1 = −k	∂ndS,

Поскольку постоянная k > 0, то из (2.13) следует, что при росте температуры в направлении вектора n (∂u/∂n > 0) поток тепла имеет противоположное направление

(dQ1 < 0).

Пусть S граница V , n внешняя нормаль к S, тогда по закону Фурье через S

в V за время dt поступает количество тепла
		∂u
Q1 = ZS	k		dSdt = ZS	(k grad u, n) dSdt,
		∂n
				∂u
По определению (grad u, n) = ru · n =					nα, α = 1, 2, 3, nα проекция вектора
				∂xα

нормали на ось xα. При этом div(p grad u) = r · (pru).

6

М.А. Греков	Уравнения математической физики
В силу формулы Гаусса Остроградского
	Q1 = Z	r · (kru)dV dt.

V

Кроме того, источники выделяют количество тепла

Z

Q2 = F (x, t)dV dt.

V

Изменение температуры u за время dt в каждой точке x равно

∂u u(x, t + dt) − u(x, t) = du|x = ∂t dt.

При этом изменении выделяется или поглощается некоторое количество тепла

Z

Q3 = cρ∂u∂t dV dt,

V

где c = c(x) количество тепла, потребляемого телом единичной массы и отнесенное к бесконечно малому изменению температуры du (т. е. c dm = cρdV, dQ3 = cρdV du).

Составляя баланс тепла, приходим к равенству

	Q3 = Q1 + Q2,
или	r · (kru) + F − cρ ∂t dV dt = 0.
VZ
		∂u

В силу произвольности V получим уравнение (2.12) при q = 0.

Для однородной среды c, ρ, k являются постоянными величинами. В этом случае

уравнение теплопроводности принимает вид

					∂u	− a2				u = f,
					∂t
где								k			F
			a2 =
									,	f =		.
							cρ				cρ
{		}				0			0	0
	Aij		=			0			0	−0	2
						0		−a2		0
						0			0	a

(2.14)

0

−a2

Аналогичный вывод уравнения (2.14) можно провести, если вместо потока тепла рассматривать поток частиц. В этом случае используется закон Нэрнста (аналог закона Фурье), согласно которому поток частиц через элемент поверхности dS за единицу

времени в направлении вектора нормали равен

dQ = −D ∂u∂t dS,

7

М.А. Греков	Уравнения математической физики

где D(x) коэффициент диффузии, u(x, t) плотность частиц в точке x в момент времени t. Уравнение для u(x, t) имеет тот же вид (2.12) и носит название уравнения диффузии. В нем ρ – коэффициент пористости, p = D, q – характеристика поглощения

среды.

2.3Стационарное уравнение

Для стационарных процессов F (x, t) = F (x), u(x, t) = u(x) уравнение колебаний (2.9)

и уравнение теплопроводности (диффузии) (2.14) принимают вид

−r · (pru) + qu = F

(2.15)

или, что то же

− div(p grad u) + qu = F,

При p = const, q = 0 уравнение (2.15) сводится к уравнению Пуассона

					F
− u = f,			f = −			.	(2.16)
					p
Aij	=	0	1	0	.
	}	1	0	0
{		0	0	1

При f = 0 уравнение (2.16) уравнение Лапласа.

Пусть в волновом уравнении

au = f

внешнее возмущение f(x, t) = f0(x)eiωt периодическое с частотой ω и амплитудой f0. Будем искать u в виде u = u0eiωt, тогда приходим к уравнению Гельмгольца:

u0 + k2u0 = −	f0(x)	, k2		ω2
			=		.
	a2			a2

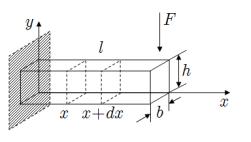
2.4Поперечные колебания тонкого прямоугольного стержня (камертона)

Дифференциальные уравнения могут иметь порядок выше второго. Рассмотрим колебание стержня, один конец которого жестко закреплен (заделан) в неподвижной недеформируемой (абсолютно жесткой) среде.

Определение формы свободных колебаний стержня и его частей сводится к решению ДУ

∂2y	+ a2	∂4y	= 0.	(2.17)
2		4
∂t		∂x

Рис. 1.2. Камертон	8

М.А. Греков	Уравнения математической физики

Приведем элементарный вывод этого уравнения. Выделим элемент стержня длины dx. Во-

первых, предполагается, что сечения, перпендикулярные оси стержня x, остаются плоскими при из-

гибе. Во-вторых, при малых деформациях длина оси стержня не меняется, то есть в момент времени t форма элемента имеет вид:

∂y

∂y

∂2y

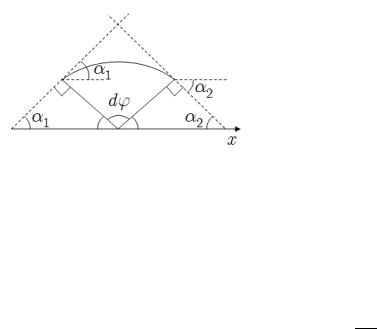
dϕ = π − (π/2 − α1 + π/2 − α2) = α1 + α2 =

∂x

x

−

∂x

x+dx

= −

∂x2

dx.

(2.18)

dl

y=η = (

R

0 +

η

dϕ

=

dl

y=0 +

ηdϕ

=

dx

+ ηdϕ.

(2.19)

|

)

|

Изменение длины элемента:

Рис. 1.3.

Полный изгибной

dl = dl|y=η − dl|y=0 = ηdϕ.

(2.20)

Сила натяжения, действующая вдоль слоя, находящегося на расстоянии η от оси x, равна

dN = EdS	dl	= Ebdη	ηdϕ	= −Eb	∂2y	ηdη,	(2.21)
	dx		dx		∂x2

где E – модуль Юнга, S – площадь. момент в сечении x равен

h/2			h/2
M = Z	ηdN = −Eb	∂2y	Z	η2dη = −EI	∂2y	,	(2.22)
		∂x2			∂x2
−h/2			−h/2

где

Zh/2

I = b η2dη = bh3 (2.23)

12

−h/2

момент инерции прямоугольного сечения относительно оси z.

Рассмотрим выделенный элемент под действием тангенциальных сил F и F + dF и моментов M и M + dM. Условие равенства нулю моментов относительно точки x + dx (точки A) приводит к равенству

	F dx = dM.					(2.24)
	Отсюда в силу равенства (2.22)
		∂M		∂3y		(2.25)
	F = ∂x = −EI			∂x3 .

9

М.А. Греков	Уравнения математической физики
Условие равенства нулю сил, действующих на элемент, включая силы инерции,
дает
		∂2y		(2.26)
	dF = ρS		dx,
		2
		∂t

где ρ плотность стержня, S площадь поперечного сечения, ρSdx масса элемента

стержня. Из (2.25) и (2.26) следует

∂2y	+ a2	∂4y	= 0,	(2.27)
2		4
∂t		∂x

где a2 = EIρS .

§ 3. Классификация линейных и квазилинейных уравнений второго порядка

Уравнения второго порядка в частных производных классифицируются в зависимости от свойств характеристических (собственных) чисел матрицы

			A11	A12
	A =		A21	A22
			. . . . . .
		An1		An2

. . . A1n

. . . A2n

. . . . . .

. . . Ann

.

Характеристические числа корни уравнения

	−			A11 − λ	A12 . . .
Det(A		λI) =		A21	A22 − λ . . .
					. . . . . .
			. . .
				An1	An2 . . .

. . .
A1n
Ann	−	λ
A2n				= 0.

Все характеристические числа симметричной матрицы A вещественны. Рассмот-

рим дифференциальное уравнение второго порядка более общего вида чем ранее:

j,k=1 Ajk(x)	∂xj ∂xk	+ Φ x1, . . . , xm, u, ∂x1		, . . . , ∂xm = 0,		(3.1)
n
X	∂2u		∂u		∂u

где Φ – произвольная функция. Уравнение (3.1) – квазилинейное. Зафиксируем точку x, в которой определены коэффициенты (3.1) и пусть в этой точке матрица A имеет α положительных, β отрицательных, γ нулевых характеристических чисел, причем α +

β + γ = n.

Определение 1. Будем говорить, что в рассматриваемой точке x уравнение (3.1) принадлежит к типу (α, β, γ). Изменение знака в (3.1) не меняет типа уравнения,

10