booklet_for_print

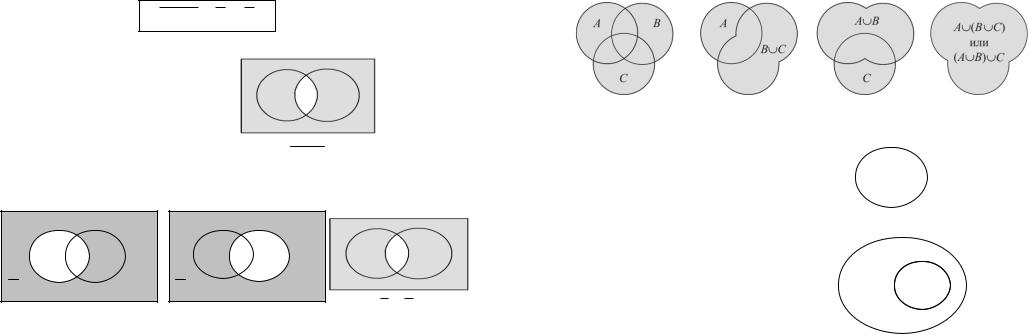
2. Второй закон де Моргана

Дополнение пересечения А и В эквивалентно объединению дополнения А и дополнения В.

А В А В (7)

Левая часть равенства:

А В

А В

Правая часть равенства:

А	В	А	В	А	В

А

В

А В

22

2.Ассоциативность:

АВ С А В С

	3. Идемпотентность:	А
	А А А

4. Если B A , то А В А

А В

Операция объединения определяется для любого количества множеств. Объединением нескольких множеств называется множество, которое состоит из всех элементов всех данных множеств и не содержит никаких других элементов.

3.2.Пересечение множеств

Если даны два множества, то можно образовать новое множество, составленное из их общих элементов. Общая часть этих множеств называется их пересечением. Пересечение множеств обозначается с помощью знака пересечения: Множества называются непересекающимися, если у них нет общих элементов, т.е. их пересечение пусто ( ).

11

Примеры:

1.А= 1,2,3 В= 2,3,4 . Пересечение множеств А и В обозначается так: А В= 1,2,3 2,3,4 = 2,3

2.М = 2,5 ; N = 3,4

M N =

3.А = В,А,С,Я ; В = И,В,А,Н,О,В

А В = В, А

4.М = x|5 x 10 ; N = x| 3 x 8 M N = x| 5 x 8

С помощью диаграмм Эйлера – Венна пересечение множеств изображается так:

С А В с		с А и с В

А С В

Определение: Пересечением двух множеств А и В называется такое множество С, которое состоит из всех элементов, содержащихся как в множестве А, так и в множестве В и не содержит никаких других элементов.

Из определения пересечения следует, что характеристическое свойство элементов множества А В составляется из характеристических свойств пересекаемых множеств с помощью союза «и».

Примеры:

1. Множество А – множество четных натуральных чисел, множество В – множество двузначных чисел. Характеристическое свойство элементов множества А – «быть четным натуральным числом», а характеристическое свойство элементов множества В – «быть двузначным числом». Тогда элементы пересечения данных множеств должны обладать свойством «быть четными и двузначными натуральными числами».

Другой вариант определения дополнения:

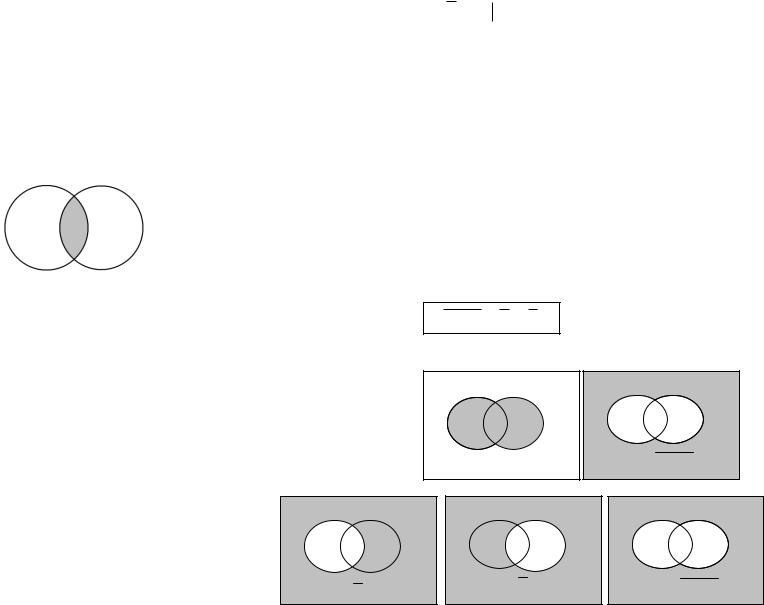
Дополнением множества А называется множество, которое состоит из тех и только тех элементов универсального множества, которые не входят в А.

A x x A , x E

Законы де Моргана

Именем де Моргана называются логические законы, связывающие дополнение объединений или пересечений множеств с дополнениями самих множеств.

Де Морган (de Morgan) (1806–1871) – шотландский математик и логик, который независимо от Джорджа Буля пришел к основным идеям математической логики.

Джордж Буль (Boole) (1815 –1864) – английский математик и логик, один из основоположников математической логики.

1. Первый закон де Моргана

Дополнение объединения А и В эквивалентно пересечению дополнения А и дополнения В.

A B A B (6)

Для иллюстрации используем диаграммы:

Левая часть равенства:

А В	А В
А В	А В

Правая часть равенства:

А	В	А	В	А В
	А		В	А В

12

21

Определение: Множество E \ A называется дополнением А до Е и

обозначается чертой вверху: A

	A E \ A
Диаграмма Эйлера-Венна выглядит так:
Свойства дополнения:									А		А
1.				A A E
2.				A A
3.			= Е
4.			E =
5.			A A

6. Если А В, то В А

7. Операции разности и дополнения связаны следующим образом:

A \ B B A

2. N – множество целых чисел, делящихся на 2, M – множество целых чисел, делящихся на 3. Тогда N M – множество целых чисел, делящихся на 6.

Свойства операции пересечения

1. Коммутативность

А В В А С

А С В

2.Ассоциативность

АВ С А В С

3. А А А

А

В А

4. Если А В , то А В А

Подобно объединению, операция пересечения определяется и для произвольного количества множеств. Пересечением нескольких множеств называется множество, которое состоит из всех элементов, содержащихся одновременно во всех данных множествах и которое не содержит никаких других элементов.

20

13

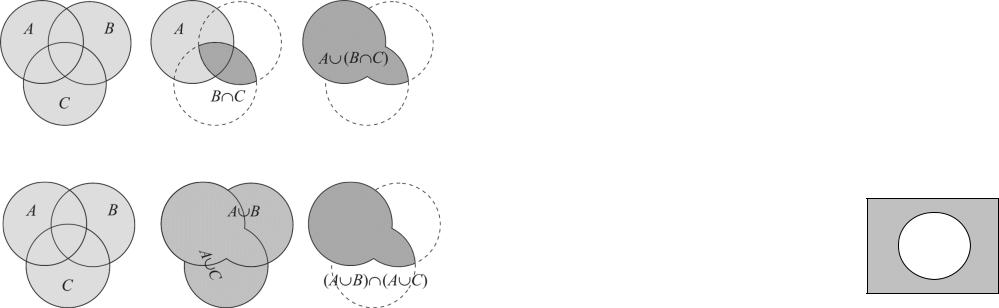
Для объединения и пересечения справедливы следующие свойства

дистрибутивности:

Теорема 1.

Для операции объединения множеств относительно операции пересечения множеств справедлив закон:

А В С А В А С	(1)

Проиллюстрируем эту теорему на диаграммах: Левая часть равенства: А В С

Правая часть равенства: А В А С

Представленные диаграммы наглядно показывают верность равенства (1). Теперь докажем это.

Доказательство:

Обозначим левую часть равенства (1) буквой Р, а правую буквой Q:

P A B C и Q A B A C .

Нам нужно доказать, что P=Q.

14

Так как y C , получаем, что y A \ B C , т.е. y P , а значит,

Q P.

Таким образом, мы доказали равенство P и Q, а значит и формулу (3).

Теорема 2.

Операции разности антидистрибутивны относительно операций объединения и пересечения:

A \ B C A \ B A \ C	(4)
A \ B C A \ B A \ C	(5)

3.4. Дополнение

Основное (универсальное) множество

Очень часто все рассматриваемые в какой-либо задаче множества являются подмножеством некоторого множества, которое мы будем называть основным (универсальным) и обозначать Е.

На диаграммах Эйлера-Венна универсальное множество Е изображается прямоуголь- Е А ником, ограничивающим рисунок. Пусть А – подмножество множества Е.

Свойства универсального множества

1.Е = Е

2.Е =

3.Е Е Е Е Е

4.Е \ Е

5.Е \ = Е

6.A E E

7.A E A

19

Пример:

Экзамен по математике сдавали 250 абитуриентов. Оценку ниже «5» получили 180 человек, а выдержали этот экзамен 210 абитуриентов. Сколько человек получили оценки «3» и «4» ?

Пусть А – множество абитуриентов, выдержавших экзамен (оценка выше «2»), В – множество абитуриентов, получивших оценки ниже «5» (оценки «2», «3», «4»). Абитуриенты, получившие оценки «3» и «4» образуют множество А В (т.е. оценки выше «2» и ниже «5»), по формуле Грассмана найдем |А В|.

|А|= 210 |В|= 180 |А В|= 250

A B

A

B

A B

A B

= 210+ 180 – 250=140

Ответ: 140 человек получили отметки «3» и «4».

Теорема 1.

Операции разности и пересечения связаны следующим соотношением дистрибутивности:

A \ B C A C \ B C (3)

Доказательство:

Обозначим левую часть равенства P, а правую Q:

P A \ B C ; Q A C \ B C

Для того, чтобы доказать теорему, необходимо и достаточно доказать, что P=Q, т.е. P Q и Q P .

1. Докажем, что P Q . Пусть x P . Тогда x A \ B и x C . Из того, что x A \ B следует, что x A и x B . Так как x C и x A , x A C . Так как x B , x B C . Из определения

разности следует, что x A C \ B C , т.е. x Q , а значит, P

Q.

2. Докажем, что Q P. Пусть y Q . Тогда y A C и

y B C . Т.к. y A C , y A и y C . Но y B C ,

значит, y B (иначе y B C )

Так как y A и y B , получаем, что y A \ B . 18

Из определения равенства двух множеств (§ 2) вытекает, что для доказательства равенства (1) надо установить два включения: P Q

и Q P .

1. Докажем, что P Q . Для этого следует показать, что любой элемент a P является элементом множества Q.

Пусть a P . Тогда так как P A B C , a A или a B C

	a A	a B C
	значит, a A B	значит, a B и a C (исходя
	и a A C (исходя	из определения операции
		пересечения) a B A и
	из определения операции
		a C A (исходя из
	объединения). Элемент a
	является общим для данных	операции объединения.
	множеств, и, значит,	Т.о. a B A C A , или
	принадлежит их пересечению:	a A B A C , т. е.
	a A B A C ,
		a Q
	т. е. a Q

Таким образом, в обоих случаях a Q . То есть, мы доказали, что

PQ .

2.Докажем, что Q P . Пусть b Q A B A C . Тогда b A B и b A C . Здесь также возможны два случая:

b A	b A
значит, b A B C , т.е.	значит, b A B C , т.е. b P
b P	т.к. b A B A C , но
	b A , значит b B и b C , т.е.
	b B C и, исходя из
	определения операции
	объединения, b B C A, а
	значит b P.
	15

Таким образом, в обоих случаях b P . То есть, мы доказали, что Q

P. Таким образом, установлена справедливость равенства (1), что

итребовалось доказать.

Теорема 2.

Для операции пересечения множеств относительно операции объединения множеств справедлив закон:

A B C A B A C (2)

Доказательство предлагается провести самостоятельно.

3.3. Разность множеств

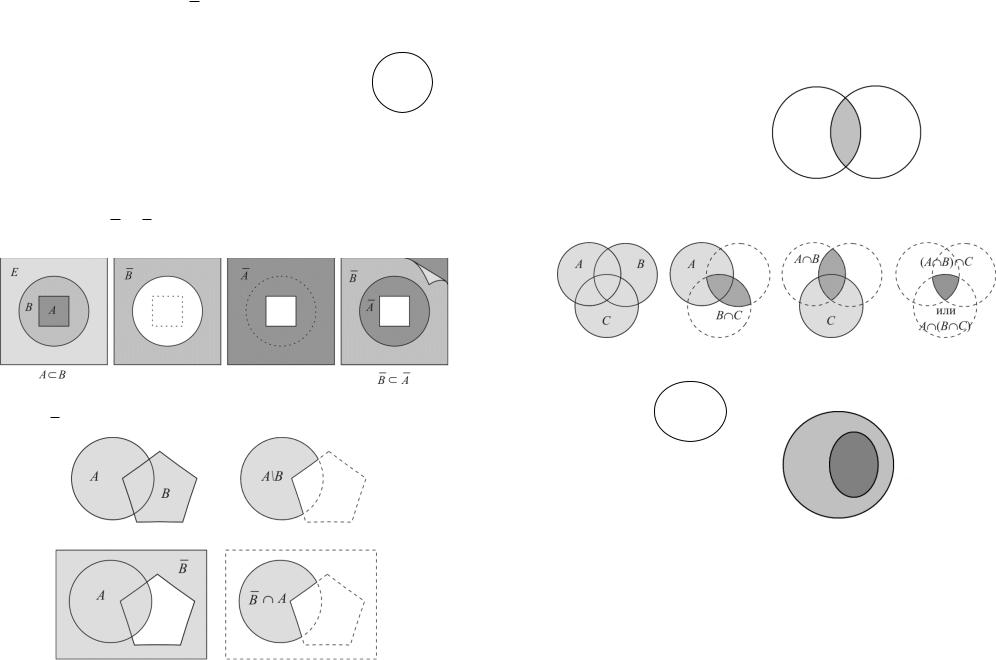
Определение: Разностью множеств А и В называется множество, состоящее из элементов, принадлежащих множеству А, но не принадлежащих множеству В. Обозначается А\В. Графически разность двух множеств выглядит так:

		А			В
		А \ В
Примеры:
1. X={2,3,4} Y={1,3,5}				X\Y={2,4}
2. А={В,А,Н,Я} В={М,А,Н,Я} А\В={В} В\А={М}
3. M={x | 5<x<10}			N={x | 7<x<15}
			M	N
		5	7	10	15		х
			M\N
M\N={x | 5<x<7}
				16

Свойства операции разности

1.	X \ =Х
2.	X \ X
3. Если X Y = , то X \ Y X		X	Y

4. Если X Y , то X \ Y =

Y

X

При решении задач часто приходится определять мощность объединения двух или нескольких множеств.

1.

Если A B = ,

то

A B

A

B

A

B

2.

Если A B ,

B

A

то

B \ A

B

A

3. Если A B , то верна формула

A B

A

B

A B

,

которая называется формулой Грассмана в честь немецкого математика Германа Грассмана (Grassmann (1809–1887)), а также формула A B A B A B

Эти формулы часто используются при нахождении числа элементов множества, заданного несколькими условиями.

17