Arkhitektonika_Vtoroy_razdel

раздел «Элементы строительной механики»

1. Основные понятия и допущения статики.

(Деформация. Твердое тело. Механическое действие. Сила. Система сил. Эквивалентная система сил. Уравновешенная система сил. Равнодействующая. Силы внешние и внутренние. Силы сосредоточенные и распределенные. Единицы измерения сил.)

Твердое тело – это тело, которое не меняет свою форму и сохраняет неизменным распределение массы внутри. В статике и вообще в теоретической механике все тела считаются абсолютно твердыми. То есть предполагается, что эти тела не деформируются, не изменяют свою форму и объем, какое бы действие на них не было оказано.

Деформация – изменение формы и размеров тела под действием приложенных сил. основана на законе Гука (каждый материал обладает определенной упругостью). Деформация проходит под воздействием внешних сил. При этом изменяется нормальное межмолекулярное взаимодействие и внутри тела возникают силы, которые противодействуют деформации и стремятся вернуть частицы тела в прежнее положение. Эти внутренние силы называют силами упругости, а свойство тел устранять деформацию после прекращения действия внешних сил называется упругостью.

Если тело не восстанавливает первоначальной формы и размеров, деформации называют пластичным. Если внутренние силы не в состоянии уравновесить внешние нагрузки, тело разрушается.

Статикой называется раздел теоретической механики, в котором излагается общее учение о силах и изучаются условия равновесия тел, находящихся под действием сил.

Прямой изгиб-деформация, вызванная силами перпендикулярными оси бруса, действующей в одной из лавных плоскостей браса, и парами сил, действующих в той же плоскости.

Кручение – это деформация, вызванная парами сил, плоскости действия которых перпендикулярна продольной оси бруса. Механические свойства – характеристики материала, описывающие его поведение при внешних силовых воздействиях. Механическим взаимодействием между телами называется тот вид взаимодействия, в результате которого происходит изменение движения этих тел или изменение их формы (деформация). Величина, являющаяся количественной мерой механического взаимодействия тел, называется в механике силой.

Силой называется физическая величина, являющаяся мерой механического взаимодействия тел. Сила – величина векторная. Она характеризуется величиной, направлением и точкой приложения. Основной единицей измерения силы является Ньютон [Н].

Внешние силы – силы взаимодействия между рассматриваемым элементом конструкции и другими телами, связанными с ним. По способу приложения делятся на:

-сосредоточенные нагрузки – силы, площадь действия которых мала по сравнению с размерами объекта. Обозначаются F (P) = Н, измеряются в кг.

-распределенные нагрузки – силы, действующие либо на некоторой длине (q = H/м, кг/см, кг/мм), либо по некоторой площади (q = H/м, кг/см2, кг/мм2), либо по объему (q = H/м, кг/см3, кг/мм3).

Разделяются по характеру изменения во времени:

-Статичные нагрузки медленно возрастают от 0 до своего конечного значения, а затем остаются неизменными. -Динамичные нагрузки сопровождаются ускорениями, как деформированного тела, так и взаимодействующих с ним сил. -Повторно-переменные нагрузки – силы, непрерывно и периодически изменяющиеся во времени.

Внутренние силы – силы взаимодействия между частицами тела, возникающие внутри элемента конструкции, как противодействие внешнему напряжению. называется напряжением. Обозначается Па-Н/м2. Во всех случаях стремятся сохранить тело, как единое целое, противодействуя всякой попытке изменить взаимное расположение частиц. Именно величиной внутренних усилий определяется возможность разрушения в том или ином сечении элемента конструкции.

Поперечная сила (F) – результирующая всех внутренних касательных напряжения в рассматриваемом сечении. Система сил - совокупность сил, действующих на какое-нибудь твердое тело.

Свободное тело – это тело, не скрепленное с другими телами, которому из данного положения можно сообщить любое перемещение в пространстве.

Если одну систему сил, действующих на свободное твердое тело, можно заменить другой системой, не изменяя при этом состояния покоя или движения, в котором находится тело, то такие две системы сил называются эквивалентными.

Система сил, под действием которой свободное твердое тело может находиться в покое, называется уравновешенной или

эквивалентной нулю.

Если данная система сил эквивалентна одной силе, то эта сила называется равнодействующей данной системы сил. Таким образом, равнодействующая - это сила, которая одна заменяет действие данной системы сил на твердое тело. Сила, равная равнодействующей по модулю, прямо противоположная ей по направлению и действующая вдоль той же прямой, называется уравновешивающей силой.

Сила, приложенная к телу в какой-нибудь одной его точке, называется сосредоточенной. Силы, действующие на все точки данного объема или данной части поверхности тела, называются распределенными.

2. Основные аксиомы статики.

(Условие равновесия тела под действием двух сил. Присоединение и отбрасывание уравновешенных сил. Закон равенства действия и противодействия.)

Аксиомы статики представляют собою результат обобщений многочисленных опытов и наблюдений над равновесием и движением тел, неоднократно подтвержденных практикой. Часть из этих аксиом является следствиями основных законов механики.

Аксиома 1. Если на свободное абсолютно твердое тело действуют две силы, то тело может находиться в равновесии тогда и только тогда, когда эти силы равны по модулю (F1 = F2) и направлены вдоль одной прямой в противоположные стороны

Аксиома 1 определяет простейшую уравновешенную систему сил, так как опыт показывает, что свободное тело, на которое действует только одна сила, находиться в равновесии не может.

Аксиома 2. Действие данной системы сил на абсолютно твердое тело не изменится, если к ней прибавить или от нее отнять уравновешенную систему сил.

Эта аксиома устанавливает, что две системы сил, отличающиеся на уравновешенную систему, эквивалентны друг другу. Следствие из 1-й и 2-й аксиом. Действие силы на абсолютно твердое тело не изменится, если перенести точку приложения силы вдоль ее линии действия в любую другую точку тела.

Аксиома 3 (аксиома параллелограмма сил). Две силы, приложенные к телу в одной точке, имеют равнодействующую, приложенную в той же точке и изображаемую диагональю параллелограмма, построенного на этих силах, как на сторонах. Величина равнодействующей

.

Конечно, 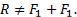Такое равенство будет соблюдаться только при условии, что эти силы направлены по одной прямой в

одну сторону. Если же векторы сил окажутся перпендикулярными, то 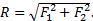Следовательно, аксиому 3 можно еще формулировать так: две силы, приложенные к телу в одной точке, имеют равнодействующую, равную геометрической (векторной) сумме этих сил и приложенную в той же точке.

Аксиома 4 (принцип противодействия). При всяком действии одного материального тела на другое имеет место такое же по величине, но противоположное по направлению противодействие.

Закон о равенстве действия и противодействия является одним из основных законов механики. Из него следует, что если тело А действует на тело В с силой 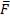, то одновременно тело В действует на тело А с такой же по модулю и направленной вдоль

той же прямой, но противоположную сторону силой . Однако силы 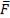и 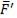не образуют уравновешенной системы сил, так как они приложены к разным телам. Эта аксиома соответствует третьему закону Ньютона: действие всегда равно и противоположно противодействию. При этом необходимо помнить, что в аксиоме 4 рассматривается случай, когда силы приложены к разным телам и в этом случае система сил не является уравновешенной в отличие от случая действия сил в аксиоме 2.

Аксиома 5 (принцип отвердевания). Равновесие изменяемого (деформируемого) тела, находящегося под действием данной системы сил, не нарушится, если тело считать отвердевшим (абсолютно твердым). Из принципа отвердения следует, что условия, необходимые и достаточные для равновесия абсолютно твердого тела, необходимы, но не достаточны для равновесия деформируемого тела, по форме и размерам тождественного с данным.

Высказанное в этой аксиоме утверждение очевидно. Например, ясно, что равновесие цепи не нарушится, если ее звенья считать сваренными друг с другом и т. д.

Аксиома 6 (аксиома связей). Всякое несвободное тело можно рассматривать как свободное, если механическое действие связей заменить реакциями этих связей (пояснения к этой аксиоме в следующем параграфе).

То, что давал преподаватель. Существует две:

1)Сумма всех проекций на ось равно 0.

2)Сумма всех моментов равна -0.

3.Виды опорных связей, их схемы, направления реакций.

(Идеально гладкая поверхность. Гибкая связь. Шарнирно-подвижная опора. Шарнирно-неподвижная опора.)

По определению, тело, которое не скреплено с другими телами и может совершать из данного положения любые перемещения в пространстве, называется свободным (например, воздушный шар в воздухе). Тело, перемещениям которого в пространстве препятствуют какие-нибудь другие, скрепленные или соприкасающиеся с ним тела, называется несвободным. Все то, что ограничивает перемещения данного тела в пространстве, будем называть связью. Например, тело лежащее на столе – несвободное тело. Связью его является плоскость стола, которая препятствует перемещению тела вниз.

Очень важен так называемый принцип освобождаемости. Любое несвободное тело можно сделать свободным, если

связи убрать, а действие их на тело заменить силами, такими, чтобы тело оставалось в равновесии.

Сила, с которой данная связь действует на тело, препятствуя тем ила иным его перемещениям, называется силой реакции (противодействия) связи или просто реакцией связи. Если в качестве физического тела рассматривать какой-либо элемент инженерного сооружения (балка, ферма, колонна, плита и т. п.), который передает давление на опоры, то реакции опор (связей) называют опорными реакциями. Реакции связей носят вторичное происхождение, они возникают как противодействие другим силам.

Все силы, кроме реакции связей, называют заданными силами Заданные силы чаще всего являются активными, т.е. силами, которые могут вызвать движение тел, например: сила тяжести, снеговая или ветровые нагрузки и т.п

Рассмотрим, как направлены реакции некоторых основных видов связей.

1.Гладкая плоскость (поверхность) или опора. Гладкой называют поверхность, трением о которую данного тела можно пренебречь.

2.Нить (гибкие связи). Связь, осуществленная в виде гибкой нерастяжимой нити, не дает телу удаляться от точки подвеса

нити. Поэтому реакция натянутой нити направлена вдоль нити от тела к точке ее подвеса. Если даже заранее можно догадаться, что реакция направлена к телу, все равно ее надо направить от тела. Таково правило. Оно избавляет от лишних и ненужных предположений и помогает установить сжат стержень или растянут.

3.Цилиндрический шарнир (подшипник). Если два тела соединены болтом, проходящим через отверстия в этих телах, то такое соединение называется шарнирным или просто шарниром; осевая линия болта называется осью шарнира.

4.Шаровой шарнир и подпятник. Этот вид связи закрепляет какую-нибудь точку тела так, что она не может совершать никаких

перемещений в пространстве. Примерами таких связей служат шаровая пята, с помощью которой прикрепляется фотоаппарат к штативу

5.Стержень. Пусть в какой-нибудь конструкции связью является стержень АВ, закрепленный на концах шарнирами.

6.Подвижная шарнирная опора. Это устройство представляет собой опорный элемент (подшипник), внутри которого вращается палец (ось) шарнира.

7.Неподвижная шарнирная опора. Реакция шарнирно-неподвижной опоры расположена в плоскости, перпендикулярной

оси возможного вращения, и ее направление определяют две взаимно перпендикулярные составляющие, соответствующие направлению выбранных осей. В строительной механике шарнирно-неподвижную опору изображают в виде двух шарнирных стержней пересекающихся в точке опоры или шарнира.

8. Неподвижная защемляющая опора или жесткая заделка. Это соединение исключает возможность каких-либо перемещений абсолютного твердого тела. Характерным для данной опоры является наличие опорного момента сил, исключающего вращение тела вокруг любой оси. Если под такую балку подвести еще одну опору, то балка станет статически неопределимой.

С помощью указанных опорных связей сооружения прикрепляются к фундаментам или отдельные элементы соединяются между собой.

4. Сложение двух сосредоточенных сил.

(Проекции силы на ось. Графический и аналитический способы сложения.)

Геометрический способ сложения сходящихся сил

Системой сходящихся сил называется система сил, линии действия которых пересекаются в одной точке. Согласно третьей аксиоме статики можно заменить одной силой –равнодействующей. Решение связано с операцией сложения векторов, в частности, сил.

Главный вектор системы сил – величина, равная геометрической сумме сил системы. Равнодействующая – всегда главный вектор, если система сил является сходящейся.

Равнодействующую плоской системы сходящихся сил можно определить графически и графоаналитически.

Сложение двух сил. При графическом определении равнодействующей на чертеже и выбранном масштабе изображаются силы, затем они складываются по правилу параллелограмма. По длине диагонали параллелограмма, учитывая выбранный масштаб, определяется равнодействующая, равная сумме слагаемых сил.

Графоаналитический способ сложения сил позволяет более точно определить равнодействующую, используя тригонометрические зависимости: - теорему косинусов:

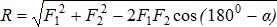или 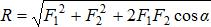(рис.1.6);

- теорему синусов: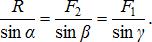

Рис. 1.6

Сложение трех сил, не лежащих в одной плоскости: геометрическую сумму 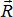трех сил 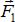, , 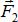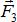не лежащих в одной плоскости, изображают диагональю параллелепипеда (рис. 1.7), построенного на этих силах (правило параллелепипеда).

Рис. 1.7

Сложение системы сил. Сложение плоской системы сходящихся сил осуществляется либо путём последовательного сложения сил с построением промежуточной равнодействующей (рис. 1.8), либо путём построения силового многоугольника (рис. 1.9).

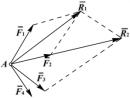Рис. 1.8 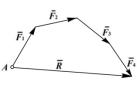Рис. 1.9

Разложение сил Разложить данную силу на составляющие – означает найти такую систему сил, для которой данная сила является равнодействующей. необходимо разложить силу по двум направлениям, лежащим в одной плоскости. На рис. 1.10 показано разложение силы F по двум направлениям ab иcd.

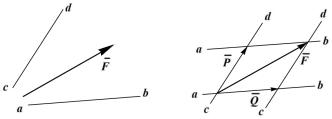Рис. 1.10

Проекция силы на ось

Проекция силы на ось – алгебраическая величина, равная произведению модуля силы на косинус угла между силой и положительным направлением оси.

Проекция Fx (рис 1.11) силы 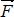на ось х положительна, если угол α острый, отрицательна - если угол α тупой. Если сила 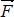перпендикулярна оси, то ее проекция на ось равна нулю.

Рис. 1.11

Аналитический способ задания и сложения сил

Аналитический способ задания сил. Для аналитического способа задания силы необходимо выбрать систему координатных

осей Охуz, по отношению к которой будет определяться направление силы в пространстве. Вектор, изображающий силу , можно построить, если известны модуль этой силы и углы α, β, γ, которые сила образует с координатными осями.

Точка А приложения силы 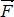задается отдельно своими координатами х, у, z. Можно задавать силу ее проекциями Fx, Fy, Fz на координатные оси. Модуль силы в этом случае определится по формуле: 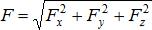, а направляющие косинусы: , , .

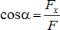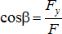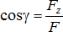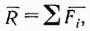
Аналитический способ сложения сил: проекция вектора суммы на какую–нибудь ось равна алгебраической сумме проекций слагаемых векторов на ту же ось, т.е., если: ,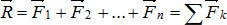

то , , .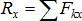

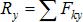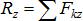Зная Rx, Ry, Rz, можем определить модуль и направляющие

косинусы: , ,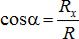

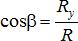5. Сложение произвольной плоской системы сходящихся сил.

(Графический и аналитический способы).

Сложение двух сходящихся сил, т. е. сил, линии действия которых пересекаются в одной точке, производится по тем же двум правилам – правилу параллелограмма и правилу треугольника, рассмотренным в главе I (§ 1), и теми же методами –

графическим, графо-аналитическим и аналитическим (методом проекций).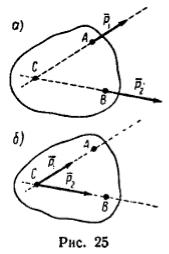 При сложении сил необходимо учитывать следующее обстоятельство.

В теоретической механике – в механике твердого тела, сила – скользящий вектор, т. е. при решении задач силу можно переносить вдоль линии ее действия в любую точку. Поэтому, если на тело действуют две силы P1 и P2, лежащие в одной плоскости, как, например, показано на рис. 25, а, то эти силы можно перенести в точку C – точку пересечения линий действия данных сил и считать их приложенными таким образом к одной точке тела (рис. 25, б), как это и сделано в задаче 20. Равнодействующую нескольких сил, сходящихся в одной точке, можно определить способом последовательного сложения. Равнодействующая такой системы сил равна геометрической сумме этих сил, т. е.

и выражается по величине и направлению вектором, замыкающим ломаную линию, стороны которой параллельны и равны данным силам. На рис. 6 показано сложение четырех сил. Многоугольник ABCDE называется силовым многоугольником.

Таким образом, применяя правило силового многоугольника, равнодействующую силу можно найти при помощи геометрического построения (графически).

Равнодействующую системы сходящихся сил можно определить и аналитическим способом (способом При этом пользуются теоремой о проекции равнодействующей силы на данную ось, согласно которой проекция равнодействующей на данную ось равна алгебраической сумме проекций слагаемых сил на ту же ось.

Применяя эту теорему для случая плоской системы сходящихся сил, находим проекции равнодействующей этих сил на две координатные оси х и у По этим проекциям определяются модуль и направляющие косинусы равнодействующей по следующим формулам:

Таким образом, при решении задачи о сложении сходящихся сил, лежащих в одной плоскости, аналитическим способом сначала нужно выбрать систему координатных осей х и у, найти углы каждой силы с координатными осями и вычислить проекции каждой силы на эти оси.

При вычислении проекции данной силы на ось необходимо иметь в виду, что абсолютное значение этой проекции равно произведению модуля силы на косинус острого угла между силой и осью проекций. При этом если направление этой проекции совпадает с положительным направлением оси, то проекция положительна; в противном случае проекция отрицательна (рис. 7). Иногда бывает удобнее знак проекции определять иначе, а именно: если направление силы составляет острый угол с положительным направлением данной оси, то проекция силы на эту ось положительна. Если же направление силы составляет острый угол с отрицательным направлением данной оси, то проекция на эту ось отрицательна. Если сила параллельна оси, то проекция силы на эту ось равна модулю силы, взятому со знаком плюс или минус в зависимости от того, какой угол (О или 180) составляет сила с положительным направлением оси. Если сила перпендикулярна к оси, то проекция силы на эту ось равна нулю.

Пример 3. Определить модуль и направление равнодействующей плоской системы сил приложенных в точке А, если и если извеетны углы между этими силами 60° (рис. 8, а).

Решение. Решим эту задачу аналитическим способом. Для этого построим систему координатных осей , направив ось по линии действия силы . Вычислим проекции искомой равнодействующей на оси и у по формулам (7

6. Условия равновесия плоской системы сходящихся сил.

(В графической и аналитической формах).

Из законов механики следует, что твердое тело, на которое действуют взаимно уравновешенные внешние силы, может не только находиться в покое, но и совершать движение, «по инерции». Таким движением будет, например, поступательное равномерное и прямолинейное движение тела.

Условиям равновесия статики удовлетворяют силы, действующие как на покоящееся тело, так и на тело, движущееся «по инерции». Для равновесия сходящейся системы сил необходимо равенства 0 алгебраических сумм проекций всех сил данной системы на каждую из координатных осей. Для плоской системы сил пропадает условие, связанное с осью Z. Условия равновесия позволяют проконтролировать, находится ли в равновесии заданная система сил.

Для равновесия системы сходящихся сил необходимо и достаточно, чтобы равнодействующая этих сил была равна нулю. 1) Геометрическое условие равновесия сходящейся системы сил: для равновесия системы сходящихся сил необходимо и достаточно, чтобы силовой многоугольник, построенный из этих сил, был замкнут (конец вектора последней слагаемой силы должен совместиться с началом вектора первой слагаемой силы). Тогда главный вектор системы сил будет равен нулю

().

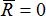2) Аналитические условия равновесия. Модуль главного вектора системы сил определяется по

форм 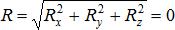. Поскольку 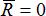, то подкоренное выражение может быть равно нулю только в том случае, если каждое слагаемое одновременно обращается в нуль, т.е. Rx = 0, Ry = 0, Rz = 0.

Следовательно, для равновесия пространственной системы сходящихся сил необходимо и достаточно, чтобы суммы проекций этих сил на каждую из трёх координат осей были равны нулю:

Для равновесия плоской системы сходящихся сил необходимо и достаточно, чтобы суммы проекций сил на каждую из двух координатных осей были равны нулю:

Теорема о трех силах: если твердое тело находится в равновесии под действием трех непараллельных сил, лежащих в одной плоскости (рис. 1.13), то линии их действия пересекаются в одной точке (необходимое условие равновесия твердого тела).

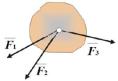Рис. 1.13

Это условие равновесия не является достаточным, т.к. равнодействующая этих сил может оказаться не равной нулю. Достаточным условием является наличие замкнутого силового треугольника при одновременном пересечения линий действия трех сил в одной точке.

Рассмотрим тело, на которое действуют три непараллельные силы 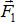, 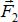и 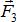(рис. 1.14).

Рис. 1.14 Так как эти силы непараллельны, то две любые силы, например, и 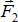должны пересечься в некоторой точкеА. Перенесём силы 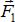и 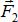вдоль линии их действия и приложим их к точке А. Заменим сходящиеся силы 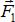и 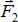их равнодействующей .

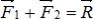Следовательно, теперь на тело действуют только две силы 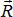и 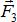. Поскольку тело находится в равновесии под действием двух сил, то согласно первой аксиоме статики, эти силы должны

действовать вдоль одной прямой АВ. Таким образом, линия действия силы 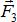должна проходить

через точку А.

7. Момент силы относительно точки.

(Определение момента. Знак момента.)

Момент (М) – сила, действующая с каким-либо плечом.. М бывает крутящим и изгибающим.

Крутящий М – результирующая силы всех внутренних касательных напряжений в рассматриваемом сечении и равен сумма всех внешних М, приложенных в одну сторону сечения.

По часовой стрелке М имеет «-»; против часовой – «+» Изгибающий М возникает в результате деформации.

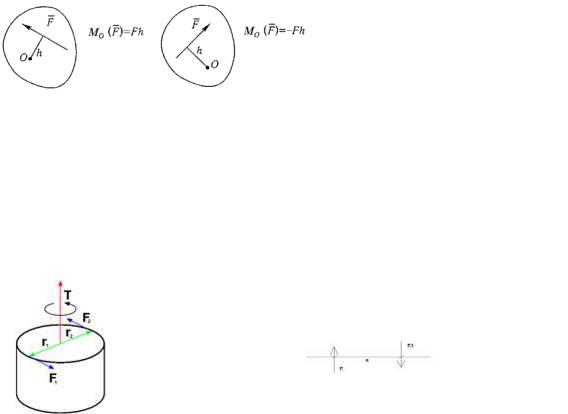
Если под действием приложенной силы твердое тело может совершать вращение вокруг некоторой точки, то для того, чтобы охарактеризовать вращательный эффект силы вводится понятие – момент силы относительно точки (или центра). Моментом силы относительно точки называется векторное произведение радиус-вектора точки приложения силы на вектор силы. Mo(F) = r х F

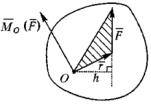Рисунок 1.1 Точка, относительно которой рассматривается момент силы, называется центром момента.

Из приведенной выше формулы очевидно, что единицей измерения момента силы является ньютон × метр (Нм).

Вектор момента направлен перпендикулярно плоскости, в которой лежат сила и точка, в ту сторону, откуда поворот от действия силы виден происходящим против хода часовой стрелки.

Вектор момента характеризует положение плоскости и направление вращательного действия силы, а также дает меру этого действия:

|Mo(F)| = F r sinα = F h,

где h – плечо силы (кратчайшее расстояние от точки O – центра момента – до линии действия силы). Если сила проходит через точку, то ее момент относительно этой точки равен нулю. Момент силы относительно точки не меняется от переноса силы вдоль линии ее действия. М0(F) = Fh, где h – плечо силы относительно точки 0.

Если силы расположены в одной плоскости, то используется понятие алгебраического момента силы. Алгебраическим моментом силы относительно точки (или центра) называется взятое со знаком плюс или минус произведение модуля силы на плечо (рисунок 1.2).

Знак плюс выбирается в том случае, если сила стремится поворачивать плоскость относительно центра момента против хода часовой стрелки.

Рис 1.2

8. Понятие пары.

(Определение. Момент пары. Эквивалентность пар. Условие равновесия системы пар.)

Парой сил называются две равные и параллельные силы, направленные в противоположные стороны и не лежащие на одной прямой.

Система сил, линии действия которых, лежат в одной плоскости, называется плоской системой сил.

Пара сил- 2 силы F и F1

Кратчайшее расстояние между линиями действия сил называется плечом пары, поэтому можно сказать, что момент пары сил по абсолютному значению равен произведению одной из сил на ее плечо.

а – плечо пары (расстояние между силами) r1+r2

Действие пары сил на твердое тело, стремится вращать это тело. Способность пары сил производить вращение определяется моментом пары, равным произведению силы на кратчайшее расстояние (взятое по перпендикуляру к силам) между линиями действия сил. Обозначим момент пары М, а кратчайшее расстояние между силами а, тогда абсолютное значение момента:

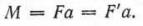M =F*a– момент пары Пара характеризуется моментом F= -F

Действие, оказываемое парой сил на твёрдое тело, характеризуется её моментом, который изображается вектором T, равным по

абсолютной величине .Момент силы относительно данной точки положителен, если сила стремится вращать тело вокруг этой точки против часовой стрелки, и отрицателен в противоположном случае. Если линия действия силы проходит через некоторую точку, то относительно этой точки плечо силы и ее момент равны нулю

Сумма проекций сил пары на ось x и на ось у равна нулю, поэтому пара сил не имеет равнодействующей, ее нельзя уравновесить одной силой, тело находиться не в равновесии. Момент пары измеряется в ньютонометрах (Н*м) или в единицах, кратных ньютонометру: кН*м

Эквивалентность пар

Две пары сил считаются эквивалентными в том случае, если после замены одной пары другой парой механическое состояние тела не изменяется, т. е. не изменяется движение тела или не нарушается его равновесие.

Эффект действия пары сил на твердое тело не зависит от ее положения в плоскости. Таким образом, пару сил можно переносить в плоскости ее действия в любое положение.

Рассмотрим еще одно свойство пары сил, которое является основой для сложения пар.

Не нарушая состояния тела, можно как угодно изменять модули сил и плечо пары, только бы момент пары оставался неизменным.

равновесие пар сил на плоскости

Подобно силам, пары можно складывать. Пара, заменяющая собой действие данных пар, называется результирующей.

момент результирующей пары равен алгебраической сумме моментов составляющих пар.

для равновесия системы пар необходимо и достаточно, чтобы момент результирующей пары равнялся нулю или чтобы

алгебраическая сумма моментов пар равнялась нулю: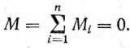

9. Приведение к центру одной силы.

(На примере внецентренно сжатой стойки. Понятие присоединенной пары.)

Решим теперь задачу о приведении произвольней системы сил к данному центру, т. е. о замене данной системы сил другой, ей эквивалентной, состоящей из одной силы (главного вектора) и одной пары (главного момента).

Пусть на твердое тело действует произвольная система сил (рис. 40, а).

Выберем какую-нибудь точку О за центр приведения и, пользуясь теоремой, перенесем все силы в центр О, присоединяя при этом соответствующие пары (см. рис. 37, б). Тогда на тело будет действовать система сил

приложенных в центре О, и система пар, моменты которых согласно формуле равны:

Рис. 40

Сходящиеся силы, приложенные в точке О, заменяются одной силой R, приложенной в точке О. При этом или, согласно равенствам (19),

Чтобы сложить все полученные пары, надо сложить векторы моментов этих пар. В результате система пар заменится одной парой, момент которой или, согласно равенствам (20),

Как известно, величина R, равная геометрической сумме всех сил, называется главным вектором системы величина равная геометрической сумме моментов всех сил относительно центра О, называется главным моментом системы сил относительно этого центра.

Таким образом, мы доказали следующую теорему о приведении системы сил: любая система сил, действующих

на абсолютно твердое тело, при приведении к произвольно выбранному центру О заменяется одной силой R, равной главному вектору системы сил и приложенной в центре приведения О, и одной парой с моментом равным главному моменту системы сил относительно центра О (рис. 40, б).

Заметим, что сила R не является здесь равнодействующей данной системы сил, так как заменяет систему сил не одна, а вместе с парой.

Из доказанной теоремы следует, что две системы сил, имеющие одинаковые главные векторы и главные моменты относительно одного и того же центра, эквивалентны (условия эквивалентности систем сил).

Отметим еще, что значение R от выбора центра О, очевидно, не зависит. Значение же при изменении положения центра О может в общем случае изменяться вследствие изменения значений моментов отдельных сил. Поэтому всегда необходимо указывать, относительно какого центра определяется главный момент.

???Рассмотрим в заключение два частных случая: 1) если для данной системы сил то она приводится к одной паре сил с моментом . В этом случае значение не зависит от выбора центра О, так как иначе получилось бы, что одна и та же система сил заменяется разными, не эквивалентными друг другу парами, что невозможно; 2) если для данной системы сил приводится к одной силе, т. е. к равнодействующей, равной R и приложенной в центре О

10. Приведение к центру плоской системы произвольных сил.

(Понятие главного вектора и главного момента.)

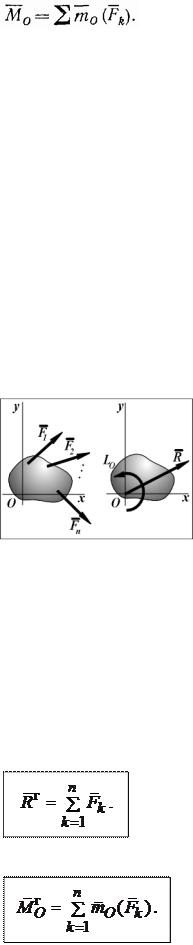
Рассмотрим плоскую систему сил (F1, F2,..., Fn),действующих на твердое тело в координатной плоскости Oxy.

Главным вектором системы сил называется вектор R, равный векторной сумме этих сил:

R = F1 + F2 + ... + Fn = 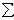Fi.

Для плоской системы сил ее главный вектор лежит в плоскости действия этих сил.

Главным моментом системы сил относительно центра O называется вектор LO, равный сумме векторных моментов этих сил относительно точки О:

LO = MO(F1) + MO(F2) + ... + MO(Fn) = 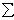MO(Fi).

Вектор R не зависит от выбора центра О, а вектор LO при изменении положения центра О может в общем случае изменяться. Для плоской системы сил вместо векторного главного момента используют понятие алгебраического главного

момента. Алгебраическим главным моментом LO плоской системы сил относительно центра О, лежащего в плоскости действия сил, называют сумму алгебраических моментов этих сил относительно центра О.

Главный вектор и главный момент плоской системы сил обычно вычисляется аналитическими методами.

Главным вектором системы сил называется вектор, равный геометрической сумме векторов всех сил системы. Главный вектор не является силой. Это свободный вектор, полученный формальным сложением перенесенных в любую точку векторов сил системы:

(1.2)

Главным моментом системы сил относительно некоторой точки О называется приложенный в этой точке вектор, равный геометрической сумме моментов всех сил системы относительно этой точки:

11.Геометрические и аналитические условия равновесия плоской произвольной системы сил. Три вида уравнений статики.

Первая форма условий равновесия

Для равновесия произвольной плоской системы сил, приложенных к твердому телу, необходимо и достаточно, чтобы главный вектор R этих сил и их главный момент Mo относительно произвольной точки O, лежащей в плоскости действия этих сил, были равны нулю, т.е.

ΣFk = 0, ΣMo(Fk) = 0

В координатной форме эти условия выражаются следующими тремя уравнениями:

ΣFkx = 0, ΣFky = 0, ΣMo(Fk) = 0.	(1.4)
Уравнения (1.4) носят название первой формы условий равновесия для произвольной плоской системы сил.

Равновесие плоских систем сил, расположенных произвольно на плоскости, можно выразить еще в двух других эквивалентных формах необходимых и достаточных условий равновесия

Вторая форма условий равновесия (теорема о трех моментах)

Теорема о трех моментах – алгебраическая сумма моментов сил относительно трех произвольных точек A,B,C, не лежащих на одной прямой, равна нулю, т.е.

ΣMA(Fk) = 0, ΣMB(Fk) = 0, ΣMC(Fk) = 0; (1.5)

Необходимость этих условий очевидна, т.к. если плоская система сил находится в равновесии, то выполняется первая форма условий равновесия (1.4)

А тогда из последнего равенства (1.4) следует, что сумма моментов всех сил относительно любой точки, следовательно, и точек А, В, С равняется нулю, т.е. выполняются условия (1.5).

Достаточность условий (1.5) следует из того, что если выполняются условия (1.5), а данная система сил не находится в равновесии, то она должна была бы приводиться к равнодействующей, одновременно проходящей через точки А, В, С.

Это невозможно, т.к. точки А, В, С не лежат на одной прямой. Следовательно, если выполняются условия (1.5), то имеет место равновесие.

Необходимым и достаточным условием равновесия системы сил является равенство нулю главного вектора и главного момента

для равновесия плоской системы сил необходимо и достаточно, чтобы алгебраические суммы проекций всех сил на две координатные оси и алгебраическая сумма моментов всех сил относительно произвольной точки равнялись нулю. Второй формой уравнения равновесия является равенство нулю алгебраических сумм моментов всех сил относительно любых трех точек, не лежащих на одной прямой.

Для плоской системы сил (например, в плоскости Oxy ) из этих уравнений получаются только три:

∑xi=0;

∑yi=0; (1.21)

∑Mo=0,

Выполнение первых двух условий (1.6) означает, что главный момент данной системы сил относительно центров приведения А и В равен нулю. Такая система может иметь равнодействующую, приложенную в центре приведения, и при R*¹0 линия действия равнодействующей проходит через точки А и В (рисунок 2.2).

Рисунок 2.2

Но по третьему условию из (1.6) проекция равнодействующей на ось Оx равна нулю. Так как ось Оx (рис.2) не перпендикулярна АВ, то это последнее условие может быть выполнено только в случае, если R*=0, т.е. когда рассматриваемая система сил уравновешена.

В частном случае, если линии действия всех сил плоской системы параллельны (плоская система параллельных сил), то условия равновесия таких сил выражаются не тремя, а двумя уравнениями:

ΣFkx = 0,	ΣMo(Fk) = 0, (1.7)
причем ось Ox параллельна данным силам, или
ΣMA(Fk) = 0,	ΣMB(Fk) = 0, (1.8)