10

Неопределенный интеграл Понятие о первообразной функции

Основной задачей дифференциального исчисления было вычисление производной или дифференциала заданной функции. Интегральное исчисление, к изучению которого мы переходим, решает обратную задачу, а именно, отыскания самой функции по ее производной или дифференциалу. То есть, имея dF(х)= f(х)d (7.1) или F ′(х)= f(х),

где f(х) - известная функция, надо найти функцию F(х).

Будем считать дальше, что равенство (7.1) выполняется на некотором конечном или бесконечном промежутке. Искомая функция F(х) называется первообразной функцией по отношению к функции f(х). Таким образом, можем записать следующее определение.

Определение: Функция F(х) называется первообразной функции f(х) на отрезке [a,b], если во всех точках этого отрезка выполняется равенство: F′(х) = f(х) или dF(х)= f(х)d.

Например, одной из первообразных функций для функции f(х)=3х² будет F(х)= х³, т.к. (х³)′=3х². Но первоообразной для функции f(х)=3х² будет также и функции и , т.к. .

Итак, данная функция f(х)=3х² имеет бесконечное множество первоообразных, каждая из которых отличается лишь на постоянное слагаемое. Покажем, что этот результат имеет место и в общем случае.

Теорема Две различные первообразные одной и той же функции, определенной в некотором промежутке, отличаются одна от другой на этом промежутке на постоянное слагаемое.

Доказательство

Пусть функция f(х) определена на промежутке (a¸b) и F₁(х) и F₂(х) - первообразные, т.е. F₁′(х)= f(х) и F₂′(х)= f(х).

Тогда F₁′(х)=F₂′(х) F₁′(х) - F₂′(х) = (F₁′(х) - F₂ (х))′= 0.  F₁(х) - F₂(х)=С

Отсюда, F₂(х) = F₁(х)+С

где С - константа (здесь использовано следствие из теоремы Лагранжа).

Теорема, таким образом, доказана.

Геометрическая иллюстрация. Если у = F₁(х) и у = F₂(х) – первообразные одной и той же функции f(х), то касательная к их графикам в точках с общей абсциссой х параллельны между собой (рис. 7.1).

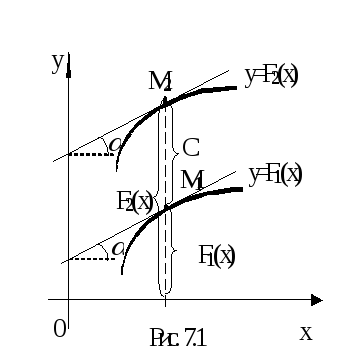
В таком случае расстояние между этими кривыми вдоль оси Оу остается постоянным F₂(х) - F₁(х)=С, то есть эти кривые в некотором понимании "параллельны" одна другой.

Следствие. Прибавляя к какой-то первообразной F(х) для данной функции f(х), определенной на промежутке Х, все возможные постоянные С, мы получим все возможные первообразные для функции f(х).

Итак, выражение F(х)+С, где , а F(х) – некоторая первообразная функции f(х) включает все возможные первообразные для f(х).

Пример 1. Проверить, являются ли функции первообразными для функции

Решение:

Ответ: первообразными для функции будут функции и

Определение: Если функция F(х) является некоторой первообразной для функции f(х), то множество всех первообразных F(х)+ С называют неопределенным интегралом от f(х) и обозначают:

∫f(х)dх.

По определению:

f(х) - подынтегральная функция,

f(х)dх - подынтегральное выражение

Из этого следует, чтоо неопределенный интеграл является функцией общего вида, дифференциал которой равен подынтегральному выражению, а производная от которой по переменной х равна подынтегральной функции во всех точках .

С геометрической точки зрения неопределенный интеграл представляет собой семейство кривых, каждая из которых получается путем сдвига одной из кривых параллельно самой себе вверх или вниз, то есть вдоль оси Оу (рис. 7.2).

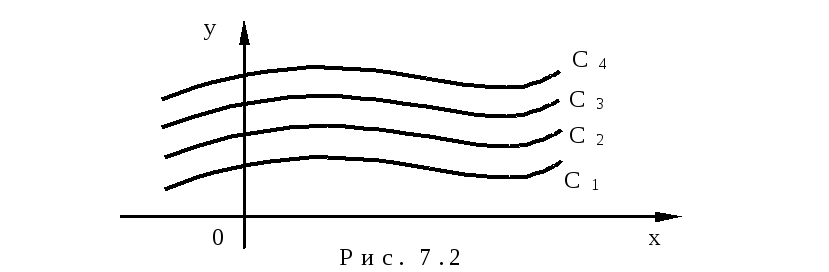
Операция вычисления неопределенного интеграла от некоторой функции называется интегрированием этой функции.

Отметим, что если производная от элементарной функции всегда является элементарной функцией, то первоообразная от элементарной функции может не представляться при помощи конечного числа элементарных функций.

Рассмотрим теперь свойства неопределенного интеграла.

Из определения 2 вытекает:

1. Производная от неопределенного интеграла равна подынтегральной функции, то есть, если F′(х) = f(х), то

. (7.3)

2. Дифференциал от неопределенного интеграла равен подынтегральному выражению

. (7.4)

Из определения дифференциала и свойства (7.3)

.

3. Неопределенный интеграл от дифференциала некоторой функции равен этой функции с точностью до постоянного слагаемого, то есть (7.5)

Справедливость (7.5) легко проверить дифференцированием (дифференциалы от обеих частей равенства равны ).

Замечания. В формулах (7.4) и (7.5) знаки и которые стоят рядом, уничтожают друг друга (если не учитывать постоянного слагаемого в (7.5)). В этом понимании дифференцирование и интегрирование являются взаимно обратными математическими операциями.

4. Отличный от нуля постоянный множитель можно выносить за знак неопределенного интеграла, то есть, если , то

(7.6)

Свойство проверяется дифференцированием обеих частей.

5. Интеграл от алгебраической суммы двух функций равен сумме интегралов от этих функций, то есть (7.7)

Для доказательства также надо взять производные от обеих частей и убедиться, что они равны между собой.

Это свойство остается верным для любого конечного числа слагаемых.

При вычислении неопределенных интегралов полезно применять такие правила:

Если , то

1. . (7.8)

2. (7.9)

3. . (7.10)

Правила доказываются дифференцированием правых и левых частей равенств (7.8 – 7.10).

Таблица интегралов