
ОСНОВНЫЕ ПОНЯТИЯ ВЕКТОРНОЙ АЛГЕБРЫ
Скалярные и векторные величины
Из курса элементарной физики известно, что некоторые физические величины, такие как температура, объем, масса тела, плотность и т.д., определяются только числовым значением. Такие величины называются скалярными величинами, или скалярами.
Для определения же некоторых других величин, таких как сила, скорость, ускорение и тому подобных, кроме числовых значений необходимо задать еще и их направление в пространстве. Величины, которые кроме абсолютной величины характеризуются еще и направлением, называются векторными.
Определение Вектором называется направленный отрезок, который определяется двумя точками: первая точка определяет начало вектора, а вторая - его конец. Поэтому еще говорят, что вектор - это упорядоченная пара точек.
На рисунке вектор изображается отрезком прямой, на котором стрелкой отмеченное направление от начала вектора к его концу. Например, рис. 2.1.
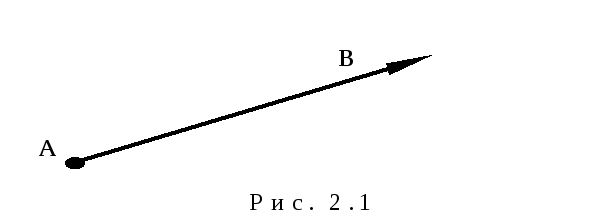 Если
начало вектора совпадает с точкой
Если
начало вектора совпадает с точкой
![]() ,
а конец с точкой
,
а конец с точкой![]() ,
то вектор обозначается
,
то вектор обозначается![]() .
Кроме этого, часто векторы обозначают
одной маленькой буквой со стрелкой над
ней
.
Кроме этого, часто векторы обозначают
одной маленькой буквой со стрелкой над
ней![]() .
В книжках иногда стрелку опускают, тогда
для обозначения вектора употребляют
жирный шрифт.
.
В книжках иногда стрелку опускают, тогда
для обозначения вектора употребляют
жирный шрифт.
К
векторам относится нулевой
вектор, у
которого начало и конец совпадают. Он
обозначается
![]() или
просто
или
просто![]() .
.
Расстояние
между началом и концом вектора называется
его длиной,
или модулем.
Модуль вектора обозначается двумя
вертикальными черточками слева:
![]() ,
или без стрелочек
,
или без стрелочек![]() или
или![]() .
.
Векторы, параллельные до одной прямой, называются коллинеарными.
Векторы, лежащие в одной плоскости или параллельные одной и той же плоскости, называются компланарными.
Нулевой вектор считается коллинеарным к любому вектору. Длина его равна 0.
Определение
Два вектора
![]() и
и![]() называются равными (рис. 2.2), если они:
называются равными (рис. 2.2), если они: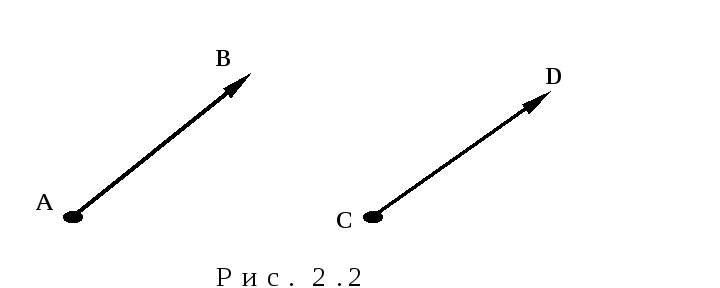 1)коллинеарны;
2) сонаправлены 3) равны по длине.
1)коллинеарны;
2) сонаправлены 3) равны по длине.
Это
записывают так:
![]() (2.1)
(2.1)
Из определения равенства векторов вытекает, что при параллельном переносе вектора получается вектор, равный начальному, потому начало вектора можно разместить в любую точку пространства. Такие векторы (в теоретической механике, геометрии), начало которых можно размещать в любой точке пространства, называют свободными. И именно такие векторы мы будем рассматривать.
Определение
Система
векторов
![]() называется линейно зависимой, если
существуют такие постоянные
называется линейно зависимой, если
существуют такие постоянные![]() ,
среди которых есть хотя бы одна отличная
от нуля, и для которых выполняется
равенство
,
среди которых есть хотя бы одна отличная
от нуля, и для которых выполняется
равенство![]() .
.
Определение Базисом в пространстве называются произвольные три некомпланарных вектора, которые взяты в определенной последовательности.
Определение
Если
![]() -
базис и вектор
-
базис и вектор![]() ,
то числа
,
то числа![]() называются
координатами вектора
называются
координатами вектора![]() в данном базисе.
в данном базисе.
Координаты
вектора будем писать в фигурных скобках
после обозначения вектора. Так, например,
![]() означает, что вектор
означает, что вектор![]() в некотором выбранном базисе имеет
разложение:
в некотором выбранном базисе имеет
разложение:![]() .
.
Из свойств умножения вектора на число и сложения векторов вытекает утверждение относительно линейных действий над векторами, которые заданы координатами.
Для
того, чтобы найти координаты вектора,
если известны координаты его начала и
конца, необходимо из соответствующей
координаты его конца отнять координату
начала.
![]()
Линейные операции над векторами
Линейными операциями над векторами называются операции сложения (вычитания) векторов и умножения вектора на число. Рассмотрим их.
Определение
Произведением вектора
![]() на число
на число![]() называется вектор, совпадающий по
направлению с вектором
называется вектор, совпадающий по
направлению с вектором![]() ,
если
,
если![]() ,
имеющий противоположное направление,
если
,
имеющий противоположное направление,
если![]() отрицательное. Длина этого вектора
равна произведению длины вектора
отрицательное. Длина этого вектора
равна произведению длины вектора![]() на модуль числа
на модуль числа![]() .
.
П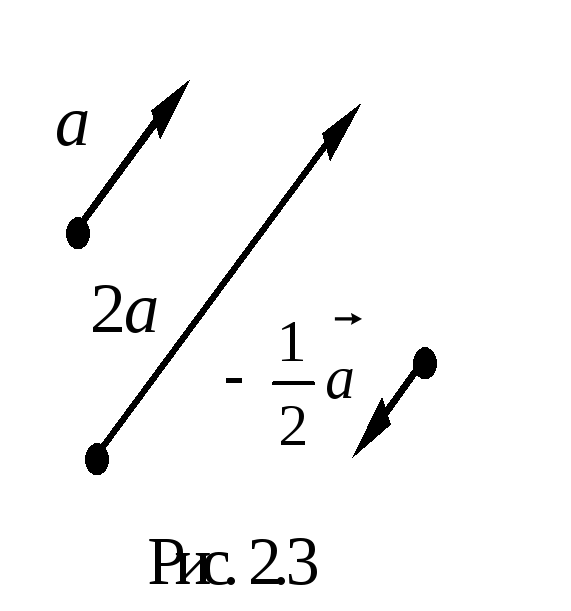 ример.
Построить вектор
ример.
Построить вектор
![]() ,
если
,
если![]() и
и![]() (рис. 2.3).
(рис. 2.3).
При умножении вектора на число его координаты умножаются на это число.
Действительно,
если
![]() ,
то
,
то
![]() .
.
Произведением
вектора
![]() на
на![]() называется вектор
называется вектор![]() ;
;![]() - противоположено направленный
- противоположено направленный![]() .
.
Отметим, что вектор, длина которого равна 1, называется единичным (или ортом).
Пользуясь
операцией умножения вектора на число,
любой вектор можно выразить через
единичный вектор того же направления.
Действительно, поделив вектор
![]() на его длину
на его длину![]() (т.е. умножив
(т.е. умножив![]() на
на![]() ),
получим единичный вектор того же
направления, что и вектор
),
получим единичный вектор того же
направления, что и вектор![]() .
Его будем обозначать
.
Его будем обозначать![]() .
Отсюда следует, что
.
Отсюда следует, что![]() .
.
Определение
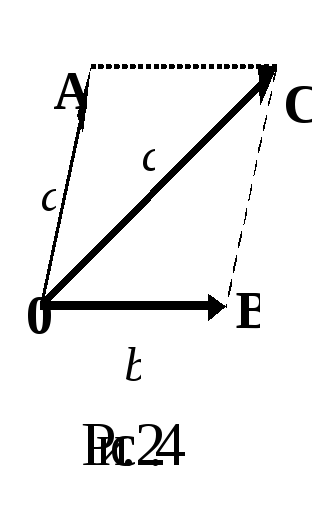
Суммой двух
векторов
![]() и
и![]() называется вектор
называется вектор![]() ,
который выходит из их общего начала и
является диагональю параллелограмма,
стороны которого векторы
,
который выходит из их общего начала и
является диагональю параллелограмма,
стороны которого векторы![]() и
и![]() (рис. 2.4).
(рис. 2.4).
![]()
 .
.
По
определению равных векторов
![]() поэтому
поэтому![]() -правило
треугольника.
Правило треугольника можно распространить
на любое количество векторов и таким
образом получить правило многоугольника:
-правило
треугольника.
Правило треугольника можно распространить
на любое количество векторов и таким
образом получить правило многоугольника:![]() - это вектор, который соединяет начало
первого вектора
- это вектор, который соединяет начало
первого вектора![]() с концом последнего вектора
с концом последнего вектора![]() (рис.
2.5).
(рис.
2.5).
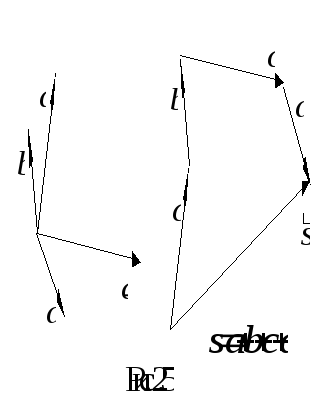
Итак, для того чтобы построить вектор суммы, надо к концу первого вектора пристроить начало второго, к концу второго пристроить начало третьего и так далее. Тогда вектором суммы и будет вектор, который соединяет начало первого из векторов с концом последнего.
При сложении векторов складываются и их соответствующие координаты
Действительно,
если
![]() и
и![]() ,
,
то
![]()
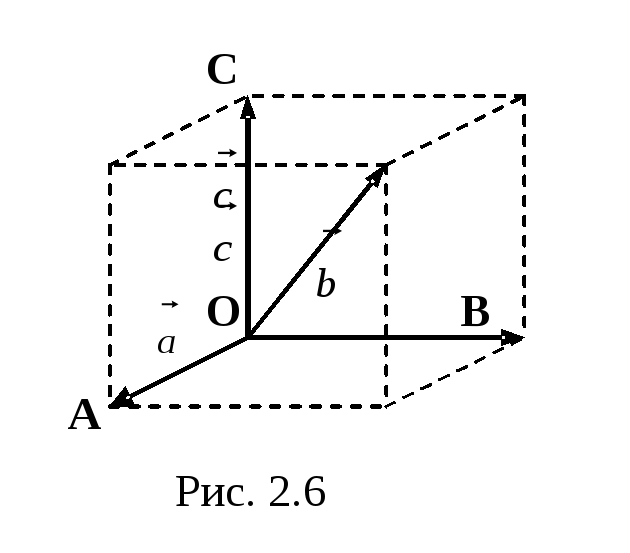
Если
векторы
![]() и
и![]() не
компланарны, то их сумма является
диагональю
не
компланарны, то их сумма является
диагональю![]() параллелепипеда, построенного на этих
векторах (рис. 2.6)
параллелепипеда, построенного на этих
векторах (рис. 2.6)
![]()
 ,
,
 где
где
Свойства:
![]() -
коммутативность;
-
коммутативность;
![]() -
ассоциативность;
-
ассоциативность;
![]()
![]() -
дистрибутивность по отношению к умножению
на число
-
дистрибутивность по отношению к умножению
на число
![]() .
.
Т.е. векторную сумму можно преобразовывать по тем же правилам, что и алгебраическую.
Определение
Разностью
двух векторов
![]() и
и![]() называют такой вектор
называют такой вектор![]() ,
который при сложении с вектором
,
который при сложении с вектором![]() дает вектор
дает вектор![]() .
Т.е.
.
Т.е.![]() если
если![]() .
Геометрически
.
Геометрически![]() представляет собой вторую диагональ
параллелограмма, построенного на
векторах
представляет собой вторую диагональ
параллелограмма, построенного на
векторах![]() и
и![]() с
общим началом и направленную из конца
вектора
с
общим началом и направленную из конца
вектора![]() в
конец вектора
в
конец вектора![]() (рис.
2.7).
(рис.
2.7).
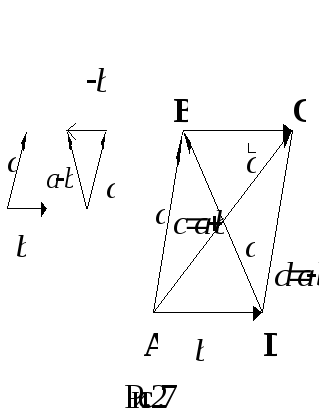
Проекция вектора на ось. Свойства проекций
Вспомним понятие числовой оси. Числовой осью называют прямую, на которой определено:
направление ( → );
начало отсчета (точка О);
отрезок, который принимают за единицу масштаба.
Пусть
имеется вектор
![]() и ось
и ось![]() .
Из точек
.
Из точек![]() и
и![]() опустим
перпендикуляры на ось
опустим
перпендикуляры на ось![]() .
Получим точки
.
Получим точки![]() и
и![]() -
проекции точек
-
проекции точек![]() и
и![]() (рис. 2.8 а).
(рис. 2.8 а).
Определение
Проекцией
вектора
![]() на ось
на ось![]() называется длина отрезка
называется длина отрезка![]() этой оси, который расположен между
основаниями проекций начала и конца
вектора
этой оси, который расположен между
основаниями проекций начала и конца
вектора![]() на ось
на ось![]() .
Она берется со знаком плюс, если
направление отрезка
.
Она берется со знаком плюс, если
направление отрезка![]() совпадает с направлением оси проекций,
и со знаком минус, если эти направления
противоположны. Обозначение:
совпадает с направлением оси проекций,
и со знаком минус, если эти направления
противоположны. Обозначение:![]() .
.
О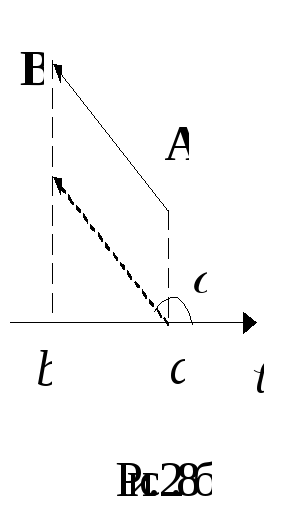 пределение
Углом между
вектором
пределение
Углом между
вектором
![]() и осью
и осью![]() называется угол
называется угол![]() ,
на который необходимо кратчайшим образом
повернуть ось
,
на который необходимо кратчайшим образом
повернуть ось![]() ,
чтобы она совпадала с направлением
вектора
,
чтобы она совпадала с направлением
вектора![]() .
.
Найдем
![]() :
:
На
рис.2.8 а представлена:
![]() .
.
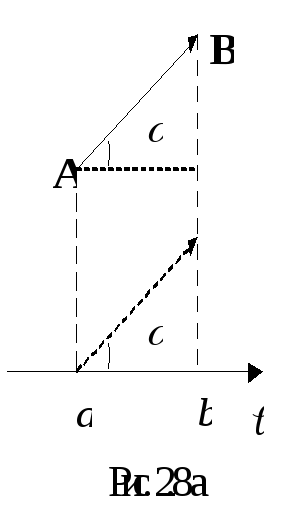
На
рис. 2.8 б):
![]() .
.
Проекция
вектора на ось равна произведению длины
этого вектора на косинус угла
между
вектором и осью проекций:
![]() .
.
Свойства проекций:
равные векторы имеют равные проекции;
при умножении вектора
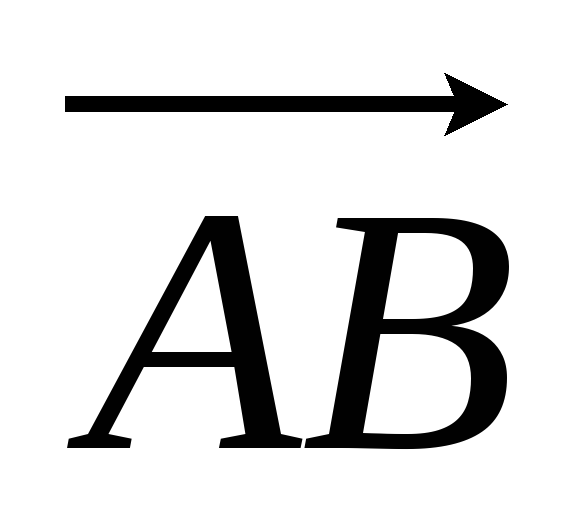 на число
на число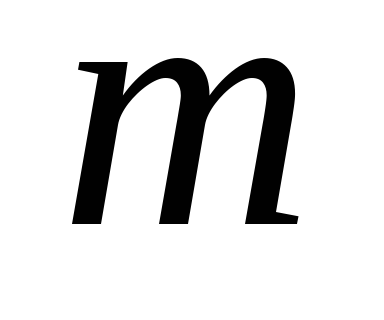 его
проекция на ось также умножается на то
же число;
его
проекция на ось также умножается на то
же число;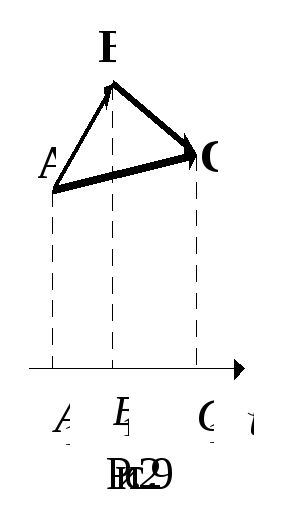 проекция
суммы двух векторов на ось равна сумме
проекций этих векторов, см. рис. 2.9.
проекция
суммы двух векторов на ось равна сумме
проекций этих векторов, см. рис. 2.9.
![]()
Если
![]() ,
то векторы называются ортогональными
,
то векторы называются ортогональными
Пример.
Заданы
векторы
![]() ,
,![]() .Тогда
.Тогда
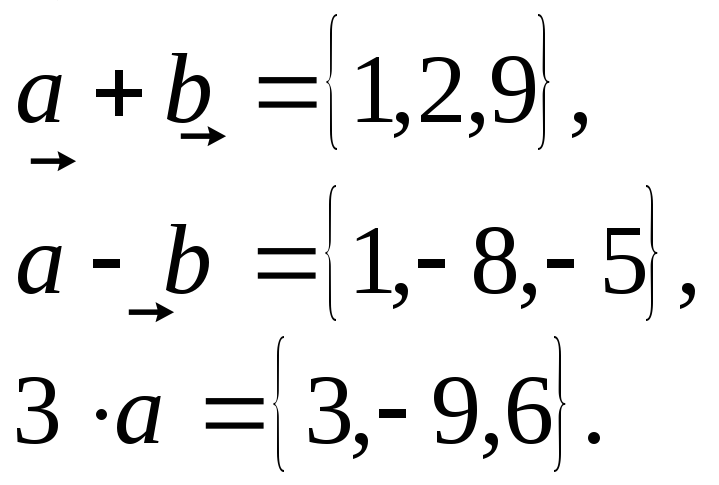 .
.
Пример.
Если начало вектора
![]() находится в точке
находится в точке![]() ,
а конец в точке
,
а конец в точке![]() ,
то вектор
,
то вектор![]() имеет координаты:
имеет координаты:
![]() .
.
О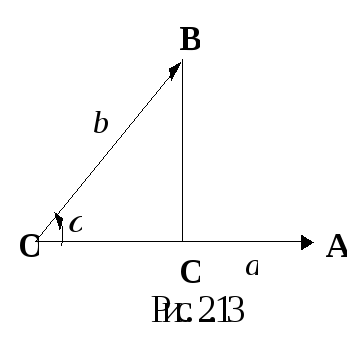 пределение
Углом между
двумя векторами
пределение
Углом между
двумя векторами
![]() и
и![]() называется наименьший угол
называется наименьший угол![]() (рис. 2.13) между этими векторами, сведенными
в общее начало
(рис. 2.13) между этими векторами, сведенными
в общее начало![]() .
.
Угол
между векторами
![]() и
и![]() символически записывают таким образом:
символически записывают таким образом: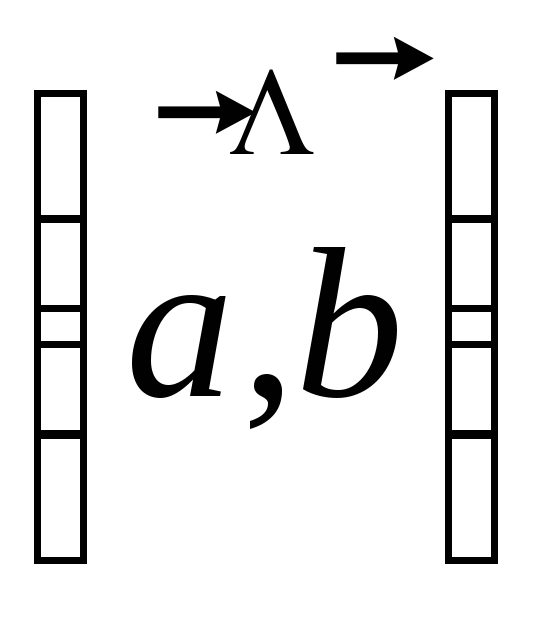 .
.
Из
определения следует, что угол
![]() между векторами может изменяться в
пределах
между векторами может изменяться в
пределах![]() .
.
Если
![]() ,
то векторы называются ортогональными.
,
то векторы называются ортогональными.
![]() .
.
Определение.
Косинусы углов вектора с осями координат
называются направляющими косинусами
вектора. Если вектор
![]() образует с осями координат углы
образует с осями координат углы![]()
![]() ,
,
откуда
![]() .
.
