5Математический_анализ

1

МАТЕМАТИЧЕСКИЙ АНАЛИЗ

1. Функция

Одним из основных математических понятий является понятие функции. Понятие функции связано с установлением зависимости (связи) между элементами двух множеств.

Если элементами множеств Х и У являются действительные числа (т. е. Х R и У R), то функцию f‚ называют числовой функцией. В дальнейшем будем изучать (как правило) числовые функции, для краткости будем именовать их просто функциями и записывать у=f(х)..

Определение Если каждому элементу х из множества Х поставить в соответствие элемент из множества У, то говорят, что на множестве Х задана функция, или функция f отображает множество Х на множество У.

Переменная х(множество Х) - аргумент или независимая переменная; переменная у (множество всех у У) - зависимая или функция.

Область определения D(f) - это	Область значений Е(f) - это множество
множество всех значений аргумента х.	всех значений зависимой переменной у.

Относительно самих величин х и у говорят, что они находятся в функциональной зависимости. Иногда функциональную зависимость у от х пишут в виде у = у(х), не вводя новой буквы (f) для обозначения зависимости.

Частное значение функции f (х) при х = а записывают так: f(а). Например, если f (х) = 2х2 — 3, то f (О) = —3, f (2) = 5.

Графиком функции у= f(х) называется множество всех точек плоскости Оху, для каждой из которых х является значением аргумента, а у — соответствующим значением функции..

Способы задания функций

Чтобы задать функцию у f (х), необходимо указать правило, позволяющее, зная х, находить соответствующее значение у.

Наиболее часто встречаются три способа задания функции: аналитический, табличный, графический.

Аналитический способ: функция задается в виде одной или нескольких формул или уравнений. Например: S = πR2; у2-4х=0.

Если область определения функции у = f(х) не указана, то предполагается, что она совпадает с множеством всех значений аргумента, при которых соответствующая формула имеет смысл.

Так, областью определения функции у = 1 õ2 является отрезок [—1; 1].

Аналитический способ задания функции является наиболее совершенным, так как к нему приложены методы математического анализа, позволяющие полностью исследовать функцию у

= f(х).

Графический способ: задается график функции.

Часто графики вычерчиваются автоматически самопишущими приборами или изображаются на экране дисплея. Значения функции у, соответствующие тем или иным значениям аргумента х, непосредственно находятся из этого графика.

Преимуществом графического задания является его наглядность, недостатком его неточность. Табличный способ: функция задается таблицей ряда значений аргумента и соответствующих значений функции. Например, известные таблицы значений тригонометрических функций, логарифмические таблицы.

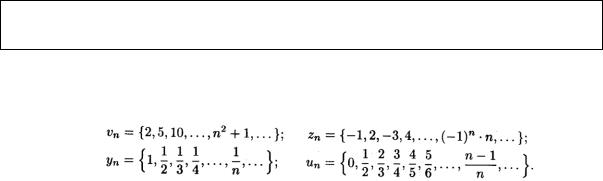
2

На практике часто приходится пользоваться таблицами значений функций, полученных опытным путем или в результате наблюдений.

Свойства функций

	Четность		Периодичность	Монотонность
	Функция называется четной,		Функция периодична,	Функция возрастающая, если
	если для x	f (x) f (x) ,	если	(x1 x2 ) f (x1 ) f (x2 ) .
	нечетной,	если	T R, x R,	Функция убывающая, если
	f (x) f (x) .	График	(x T ) D(t)	(x1 x2 ) f (x1 ) f (x2 ) .
	четной	функции	f (x T ) f (x).	Функция постоянна, если
	симметричен	относительно
			Т называется периодом	( x1 , x2 X )
	оси Оу, график нечетной -
			функции	f (x1 ) f (x2 ).
	симметричен	относительно
	начала координат.

Обратная функция

Если функция у = f (х) является взаимно-однозначным отображением множества D(f)=Х на множество D(f)=У, тогда существует обратное отображение множества Y на множество X

по правилу f 1 : y	x ,	x X ,	y Y,
1	1	1	1

у1- образ элемента х1, при прямом отображении; f - прямая функция;

f -1- обратная функция.

Графики взаимно-обратных функций симметричны относительно биссектрисы І и Ш координатных углов.

Примеры:

1.y e x ln y x;

2.y cosx arccosy x.

Сложная функция

Пусть функция у = f (u) определена на множестве D, а функция u = φ(х) на множестве D1, причем для любых х D соответствующее значение u = φ(х) D. Тогда на множестве D1 определена функции u = f(φ(х)), которая называется сложной функцией от х (или суперпозицией заданных функций, или функцией от функции).

Переменную u = φ(х) называют промежуточным аргументом сложной функции. Например, функция у = sin 2х есть суперпозиция двух функция у = sin u и u = 2х. Сложная

функция может иметь несколько промежуточных аргументов.

2. Числовые последовательности

Определение. Числовой последовательностью является множество значений функции у = f (х), определенной на множестве натуральных чисел.

a1 , a2 ,...,an ,..., an ;

an f (n),

n 1,2,...- запись и обозначение

последовательностей, an - общий член последовательности.

Последовательность {хn} называется ограниченной, если существует такое число М > О, что для любого n N выполняется неравенство |хn| ≤ М

В противном случае последовательность называется неограниченной.

Легко видеть, что последовательности уn, и un, ограничены, а vn и zn неограничены.

3

Последовательность {хn} называется возрастающей (неубывающей), если для любого n

выполняется неравенство an+1 > аn	(an+1 ≥ аn).	Аналогично определяется убывающая
(невозрастающая) последовательность.
Все эти последовательности	называются	монотонными последовательностями.

Последовательности уn, un и vn , монотонные, а zn - не монотонная.

Если все элементы последовательности {хn} равны одному и тому же числу с, то ее называют постоянной.

Сходящейся называют последовательность, которая имеет предел.

	Пределом последовательности		Геометрический смысл
	u1,u2,…un,… называют число а, если для	предел числовой последовательности:
	любого положительного ε существует	число а является пределом
	такое натуральное число Nε, зависимое от	последовательности					, если можно
					u	n
	ε, такое что все члены	указать такой номер N, что все члены
	последовательности с номерами n> Nε,
		последовательности с номерами
	удовлетворяют неравенству | un -а|< ε.	большими N, находятся в ε -
	Записывают lim un a.
		окрестности точки а
	n
			a-	a			a+	x
		ε - любое положительное число.

Свойства сходящихся последовательностей

1. Всякая сходящаяся последовательность ограничена и имеет единственный предел. (теорема Вейерштрасса)

2. lim (an	bn ) lim an	lim bn .
n	n	n

	a					lim an
3. lim			n			n
		b				lim b
n
		n				n	n

(lim bn 0).

n

4. lim (an bn ) lim		an lim bn .
n	n	n

3. Предел функции.

Рассмотрим функцию у = f (х), определенную в некоторой окрестности точки х0 кроме, возможно, самой этой точки.

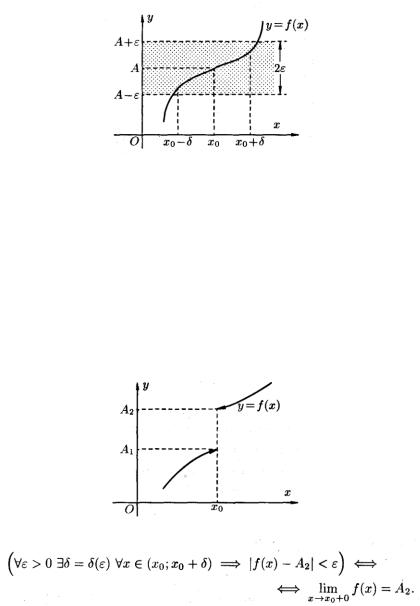
Определение. Число A называют пределом функции у = f (х), в точке (при x x0 ),

если для произвольного ε >0, найдется соответствующее нему число δ >0, что для всех х≠х0, которые удовлетворяют неравенству |х – х0|< δ, будет выполняться | f (х) - А|< ε.

f(x)			y=f(x)
A+
A			min 1 ; 2
A-
	x0+ 1	x0	x0+ 2	x

4

Записывают lim f (x). =А.

x x0

Геометрический смысл предела функции: А = lim f (x). , если для любой ε-окрестности

x x0

точки А найдется такая δ -окрестность точки х0, что для всех х≠х0 из этой δ -окрестности соответствующие значения функции f(х) лежат в ε-окрестности точки А. Иными словами, точки графика функции у = f(х) лежат внутри полосы шириной 2ε, ограниченной прямыми у = А + ε,

у =А- ε . Очевидно, что величина δ зависит от выбора ε, поэтому пишут δ = δ(ε).

Односторонние пределы

В определении предела функции lim f (x). =А считается, что х стремится к хо любым

x x0

способом: оставаясь меньшим, чем хо (слева от хо), большим, чем хо (справа от хо), или колеблясь около точки хо.

Бывают случаи, когда способ приближения аргумента х к хо существенно влияет на значение предела функции. Поэтому вводят понятия односторонних пределов.

Число А1 называется пределом функции у = f(х) слева в точке хо, если для любого число ε>0 существует число δ = δ (ε) > О такое, что при х (хо — δ; хо), выполняется неравенство

f(х) — А1 < ε. Предел слева записывают так: lim f (x). =А1 или коротко: f(х0-0)=А1

x x0 0

(обозначение Дирихле).

Аналогично определяется предел функции справа, запишем его с помощью символов:

Коротко предел справа обозначают f(хо + 0) = А2.

Пределы функции слева и справа называются односторонними пределами. Очевидно,

если существует lim f (x). = А, то существуют и оба односторонних предела, причем А= А1= А2.

x x0

Справедливо и обратное утверждение: если существуют оба предела f(х0 —0) и f(х0 +0) и они

равны, то существует предел А = lim f (x). и А—f(хо —0).

x x0

Если же А1 ≠А2, то lim f (x). не существует.

x x0

Предел функции при х →∞

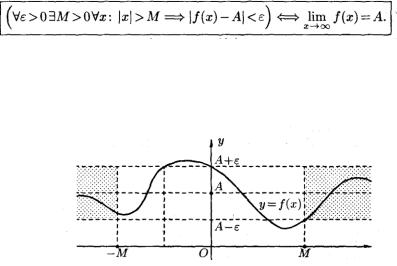
Пусть функция у = f(х) определена в промежутке (—∞; ∞). Число А называется пределом функции f(х) при х →∞, если для любого положительного числа ε существует такое число М =

5

М(ε) > О, что при всех х, удовлетворяющих неравенству х > М выполняется неравенствоf(х) — А < ε. Коротко это определение можно записать так:

Если х →+∞, то пишут А= lim	f (x)., если х →+∞, то — А = lim f (x).
x	x

Геометрический смысл этого определения таков: для ε>0 М>0, что при х(-∞;М) или х (М;+ ∞) соответствующие значения функции f(х) попадают в ε-окрестность точки А, т. е. точки графика лежат в полосе шириной 2ε, ограниченной прямыми у =А+ε и у =А—ε (см. рис.)

Бесконечно малая функция

Определение. Функция x называется бесконечно малой при x x1 или при

х→∞, если

lim x 0 или lim x 0.

x x1

x

При х→х1

это означает, что

0 0 x 0

x x1

x

.

Например (x) sin x является бесконечно малой при х→π, или х→0 т.к.

lim sin x 0

и lim sin x 0.

x

x 0

1

1

является бесконечно малой при x , т.к. lim

0.

Эта же функция

x 2

x x 2

1

при x 2 будет приобретать сколь угодно большие значения.

x 2

Бесконечно большая функция

Определение. Функция f(х) называется бесконечно большой при х→х0, то есть

lim f x , если для произвольного M 0 найдется такое 0, что

f x

M для всех

x x1

x из - окрестности точки x1. x ] x1 , x1

[ .

M 0 M 0 x 0

x x1

f x

M

.

Если важно отметить знак бесконечно большой функции, то перед символом пишут

+ или - . Например,

	lim	1				,
		x		2
	x 2 0
	lim	1				.
	x 2 0		x 2
Замечание	Постоянная величина не является бесконечно малой, какой бы мала она не
была. Только число 0 можно считать бесконечно малой величиной.
Замечание	Нельзя называть функцию ни бесконечно большой, ни бесконечно

малой, если не указана окрестность точки, где она рассматривается.

		6
Так, мы видели, что функция	1	является бесконечно малой при х→∞ и бесконечно

x 2

большой при х→2

Связь между бесконечно большими и бесконечно малыми функциями выражается такой теоремой:

Теорема. Если (x) есть функция бесконечно малая, в окрестности точки х=х0., то

1

функция (x) является бесконечно большой в окрестности этой же точки.

Сформулируем некоторые теоремы о бесконечно малых функциях.

Теорема. Алгебраическая сумма конечного числа бесконечно малых функций в окрестности точки х=х0 является бесконечно малой функцией в окрестности х=х0. Теорема 4.4. Произведение функции бесконечно малой в окрестности точки х=х0 на

функцию, ограниченную в окрестности точки х=х0, функция бесконечно малая в окрестности

точки х=х0.

Следствие 1. Произведение функции бесконечно малой в окрестности точки х=х0 на постоянную величину есть функция бесконечно малая в окрестности точки х=х0.

Следствие 2. Произведение двух бесконечно малых функций в окрестности точки х=х0.

функция бесконечно малая в окрестности точки х=х0.

Таким образом, сумма, разность и произведение конечного числа бесконечно малых функций в окрестности точки х=х0 бесконечно малая в окрестности этой же точки.

Этого нельзя сказать об их отношении. Так, если х→0, то (x) x, (x) x 2								и (x) 2x
являются бесконечно малыми в окрестности точки х=0, а их отношения при х→0:
(x)				x			,
(x)			x 2
	(x)			x2			0,
	(x)			x
	(x)			2x			2.
	(x) x
Из этого следует, что отношения двух бесконечно малых функций в окрестности точки
х=х0 представляет собой неопределенность типа					0	.
			0
Отношения двух бесконечно больших функций также представляет собой
неопределенность, которую обозначают символом							.

Для того чтобы вычислить предел отношения двух бесконечно малых или двух бесконечно больших функций, надо провести дополнительные исследования, которые

носят название раскрытия неопределенностей соответственно типа 00 и . С ними мы

познакомимся дальше.

Теорема. Если функцию f(х) имеет предел, равный А, то ее можно представить как сумму числа

А и бесконечно малой функции α(х), т.е. если

7

Теорема (обратная). Если функцию f(х) можно представить в виде суммы числа А и бесконечно малой функции α(х), то число А является пределом функции f(х), т. е. если f(х)

= А + α(х), то

Теоремы о пределах

Для вычисления пределов надо пользоваться некоторыми правилами. Эти правила формулируются в виде теорем, которые мы сформулируем ниже. Для доведения этих

теорем используется следующая теорема:

Теорема. Для того чтобы функция у=f(х) в точке х=х1 имела предел число a,

необходимо и достаточно, чтобы она была представлена в окрестности данной точки в виде суммы f (x) a (x) ,

где (x) - бесконечно малая функция в окрестности точки х=х1 .

Теорема. Предел алгебраической суммы(разности) конечного числа функций, которые имеют предел в точке х=х0 , равен сумме(разности) пределов слагаемых:

Доказательство. Пусть		Тогда по теореме о связи функции, ее
предела и б.м.в. можно записать:	и	Следовательно

Следствие Функция может иметь только один предел при х→х1

8

Теорема. Предел произведения конечного числа функций, которые имеют пределы в точке х=х1 , равен произведению пределов сомножителей:

lim	f1(x) f2	(x) lim	f1	(x) lim f2 (x).
x x1		x x1		x x1

Следствие. Постоянный множитель можно выносить за знак предела:

lim cf1	(x) c lim f1 (x) .
x x1	x x1

Следствие. Предел степени с натуральным показателем равен той же степени предела:

			lim( f (x))n (lim f1 (x))n		limxn (x1 )n
			x x1	x x1	, в частности x x1	, n N
Теорема.			Если функция у=f(х) имеет в точке х=х1			предел, отличный от нуля, то
функция	1		- ограничена в окрестности данной точки.
	f (x)

Теорема. Предел частного двух функций, имеющих пределы, равен отношению

пределов этих функций при условии, что предел знаменателя не равен нулю:

		f1 (x)		lim f1 (x)
	lim			x x1			, если	lim f2 (x) 0.
	x x1	f2 (x)		lim f2 (x)				x x1
				x x1
	Сформулируем признака существования пределов:
Теорема. Если значение функции f(х) находится между соответствующими
значениями функций f1(х) и f2(х), которые при х=х1								стремятся к одному пределу а, то f(х)
при х=х1 также имеет предел число a , т.е., если
				f1 (x) f (x) f2 (x)
						и если
		lim		f1	(x) lim f2 (x) a,
		x x1				x x1
						то
				lim f (x) a.
					x x1
					Свойства пределов
1. lim ( f (x) g(x)) lim f (x) lim g(x).
x a	x a	x a

		f (x)			lim f (x)
					x a
2.	lim
					lim g(x)
	x g(x)
					x a

3. lim	f (x) g(x) lim f (x)
x a	x a

4.	lim k f (x) k lim f (x).
	x a	x a
5.	lim( f (x))n (lim f1 (x))n
	x x1	x x1

(lim g(x) 0).

x a

lim g(x).

x a

Важные пределы

sin x

1

1 x

lim

;

lim 1

e

;

a

x

1

log a (1 x)

x

x 0

x

x

lim

ln a,

lim

log

e,

a

Первый

x 0

x

x 0

x

Второй

a 0;

a 0.

замечательный

замечательный

предел

предел

9

Эквивалентные бесконечно малые и основные теоремы о них

Среди бесконечно малых функций одного порядка особую роль играют так называемые эквивалентные бесконечно малые.

Если lim	1, то α и β называются эквивалентными бесконечно малыми (при х → хо); это
x õ0
обозначается так: α ~ β.
Например, sin х ~x при х → О, т. к lim		sin x	1 ; tg х~ х при х→ О , т.к. lim	tgx	1
	x 0	x	x 0 x

Применение эквивалентных бесконечно малых функций Вычисление пределов

Для раскрытия неопределѐнностей вида

бесконечно малых эквивалентными и функций. Как известно, sin х~x при х эквивалентных б.м .ф.

0 часто бывает полезным применять принцип замены

0

другие свойства эквивалентных бесконечно малых →х0, tg х~ х при х→ О. Приведем еще примеры

Пример.

Пример.

Пример.

Решение. Так как

то

Ниже приведены важные эквивалентности, которые используются при вычислении пределов:

10

Пример.

3. Производная функции

При изучении различных материальных процессов, например движения тела, течения химических реакций, экономических процессов (спроса и затрат), мы встречаемся с задачей определения скорости изменения соответствующих величин. В большинстве случаев такие задачи не могут быть решены с помощью элементарной математики. Для их решения пользуются дифференциальным исчислением.

Итак, рассмотрим более детально задачу о прямолинейном движении некоторого твердого тела.

Предположим, что между пройденным телом путем и временами, за который пройден этот путь, существует зависимость S = f(t).

					(5.1)
			S1		Предположим
					также, что движение
	О		А	В	началось в т.0 при t=0
		S			(рис.1).
			Рис. 5.1

За время t тело прошло путь S = f(t) и оказалось в точке А, а в следующий момент времени t+Δt оно оказалось в точке В. Обозначим путь, который прошло тело за время t+Δt, через S1. Итак, за время Δt тело прошло путь S1-S= f(t+ Δt) - f(t) Тогда средняя скорость движения тела на отрезке АВ будет определяться по формуле (5.2)

	vсер	S1	S		f (t t) f (t)	.	(5.2)
		t			t

Но эта скорость не будет мгновенной скоростью в момент t. Если говорят, например, что поезд двигается со скоростью 100 км/ч, то это не означает, что он имеет такую скорость все время, понятно, что в начале движения и в конце его скорость меньше. Чем меньше промежуток времени, на котором измеряется средняя скорость, тем ближе результат измерения к фактической скорости в момент времени t. Итак, мгновенная скорость тела в момент времени t

будет равна vм (t) lim	f (t t) f (t)	.	(5.3)
t 0	t

К такому же результату мы придем, если будем определять скорость химической реакции, скорость выпаривания вещества и т.п. Итак, разные с физической точки зрения задачи приводят к необходимости выполнения одинаковых с математической точки зрения действий, а именно, вычисления предела отношения приращения функции к приращению аргумента при условии, что последний стремится к нулю.

Приращением функции f(х) в точке х0 называется разность между значением функции в точке (x0 x) и ее значением в точке х0

f (x0 ) f (x0 x) f (x0 ) .

Определение: производной функции у=f(х) в точке х называется предел отношения

приращения функции у в точке х к приращению аргумента			х, при условии, что приращение
аргумента стремится к нулю f (x) y lim	f (x)	lim	f (x x) f (x) .
x 0	x	x 0	x