ГидравликаВиВ

При изучении движущейся жидкости применяются два метода –Лагранжа и Эйлера.

Рис.3.1. Два метода изучения движущейся жидкости: a − метод Лагранжа; b – метод Эйлера

В методе Лагранжа изучается движение каждой жидкой частицы

(рис. 3.1, а). В момент времени t0 она находится в точке А с координатами x0 , y0 , z0 ; в момент tk − в точке В с координатами xk , yk , zk . Проекции скорости частицы на координатные оси записываются как

ux	dx	;uy	dy	;uz		dz	.
	dt
			dt			dt

Если известны функции ux f1(t),uy f2(t),uz f3(t), то, проинтегрировав,

получим:

tk	tk	tk
x uxdt ;	y uydt ;	z uzdt.
t0	t0	t0

Итогом расчета является траектория частицы; она будет зависеть от времени t и начальных координат точки x0 , y0 , z0 .

В методе Эйлера определяются поля скоростей в заданном пространстве, занятом жидкостью (рис. 3.1, b), в данный момент времени, то - есть

ux f1(x, y,z,t); uy f2(x, y,z,t); uz f3(x, y,z,t).

Метод Эйлера оказывается в большинстве случаев более плодотворным, поэтому он является основным в кинематике и динамике жидкости.

3.1. Основные понятия и определения кинематики жидкости

Линией тока называется линия, проходящая через последовательно движущиеся одна за другой частицы жидкости в данный момент времени. В каждой точке линии тока вектор скорости касателен к ней ( рис. 3.2, а).

Линия тока и траектория в общем случае − различные кривые и совпадают только при установившемся движении. Поскольку в каждой точке линии тока вектор скорости касателен к ней, то бесконечно малый элемент кривой ds и вектор скорости u в данной точке можно рассматривать как параллельные прямые.

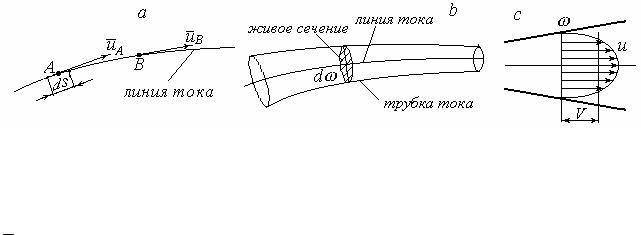
Рис.3.2.К основным понятиям кинематики жидкости: а – линия тока; b – элементарная струйка; с − поток

Условие параллельности вектора ds с проекциями dx,dy,dz и вектора скорости u с проекциями ux , uy , uz можно записать как:

dx		dy		dz	.	(3.1)
ux uy				uz

Это выражение − уравнение линии тока.

Проведем в какой – либо точке линии тока элементарную площадку dω, перпендикулярную к линии тока (рис. 3.2, b). Она называется живым сечением. Через каждую точку контура живого сечения проведем линии тока. Образованная этими линиями тока криволинейная цилиндрическая поверхность называется трубкой тока . Жидкость, заполняющая трубку тока, называется элементарной струйкой. При установившемся движении элементарная струйка обладает следующими свойствами:

во всех точках данного живого сечения скорость можно считать одинаковой;

соседние элементарные струйки не пересекаются и не перемешиваются;

с течением времени форма элементарной струйки не изменяется.

Потоком жидкости называется вся совокупность элементарных струек, протекающих по данному каналу. Живым сечением потока называется часть его поперечного сечения, занятая жидкостью. В отличие от элементарной струйки, скорость по сечению потока переменна (рис. 3.2, с).

Потоки бывают напорными и безнапорными. Напорные потоки возникают при движении жидкости в условиях избыточного давления; живое сечение трубопровода полностью заполнено жидкостью; с окружающей средой жидкость сообщения не имеет. Безнапорные потоки возникают при движении жидкости за счет собственного веса − это движение в открытых каналах, имеющих уклон. Жидкость при этом имеет свободную поверхность, граничащую с окружающей средой.

Плавно изменяющееся движение потока − такое, при котором кривизна линий тока мала, угол расхождения между ними также мал. В этом случае сечение потока можно считать плоским.

Одномерными называются такие потоки, параметры которых (скорость и давление) зависят только от одной координаты (например, от продольной координаты x). Двумерным или плоским потоком называется такой, у которого параметры зависят от двух координат − продольной и одной из поперечных (например, x и z). У трехмерного потока параметры движения −

функции трех координат. Если у трехмерного потока параметры в двух поперечных координатах изменяются одинаково, поток называется

осесимметричным.

Объемным расходом или просто расходом Q называется объем жидкости, протекающей через живое сечение потока в единицу времени:

Q W /t , м3/с. Если речь идет о расходе элементарной струйки за бесконечно малый отрезок времени dt, то можно записать: dQ dW / dt.

Связь между скоростью и расходом. Рассмотрим вначале элементарную струйку (рис. 3.3, а). В живом сечении dω1 скорость равна u.

Рис.3.3. Связь между скоростью и расходом:

a , b – для элементарной струйки; c – для потока

Пусть за время dt жидкость, находящаяся в живом сечении dω1 , пройдет путь ds и окажется в сечении dω2 . Ввиду малости ds можно считать, что площадь не изменилась, то - есть dω1 = dω2 = dω . Объем жидкости, прошедший за dt через dω1 , равен объему цилиндра: dW = ds∙dω. Разделим обе части этого выражения на dt:

dW ds d . dt dt

Так как	dW	dQ , а	ds	u, то получим связь между скоростью и расходом
	dt		dt
для элементарной струйки: dQ ud .					(3.2)

Расход через сечение потока ω (рис. 3.3, с) можно найти, просуммировав (то - есть проинтегрировав) расходы всех элементарных струек потока по всей площади живого сечения:

Q ud .	(3.3)
Для интегрирования необходимо знать закон изменения скорости по

сечению потока (математическое описание подинтегральной функции u). Для решения многих практических задач знание всей эпюры скоростей необязательно − достаточно знать среднюю скорость V потока в сечении . Средней скоростью потока в данном сечении называется такая

фиктивная скорость V, постоянная по всему сечению, при которой расход через данное сечение равен истинному, определяемому интегралом (3.3).

Заменим в выражении (3.3)	u на V. Поскольку V = const, V можно
вынести за знак интеграла и получить:
Q = V∙ω .	(3.4)

Это выражение определяет связь между расходом и средней скоростью для потока.

Уравнение постоянства расхода при установившемся движении

Рассмотрим вначале элементарную струйку несжимаемой жидкости (ρ = const). Пусть два ее живых сечения dω1 и dω2 расположены на таком расстоянии друг от друга, когда пренебречь различием в площадях dω1 и dω2 нельзя (рис. 3.3, b). За время dt через сечение dω1 втекает в объем А

дополнительный объем dW1 = dQ1 dt = u1 d ω1dt. За это же время через сечение dω2 вытекает объем dW2 = dQ2 dt = u2 dω2 dt. Очевидно, что dW1 = dW2 .

Если бы за отрезок времени в ограниченный объем струйки втекало жидкости больше, чем вытекало, струйка стала бы толще, если наоборот − тоньше. Оба этих варианта противоречат свойству элементарной струйки сохранять

свою форму при установившемся движении. Отсюда следует: dQ1	= dQ2 или
u1d 1 u2d 2.	(3.5)
Проведя аналогичные рассуждения для потока , имеющего в живых
сечениях ω1 и ω2 средние скорости соответственно V1 и V2 , получим
выражение для уравнения постоянства расхода для потока:
V1 1 V2 2.	(3.6)

3.2. Дифференциальное уравнение неразрывности для идеальной жидкости

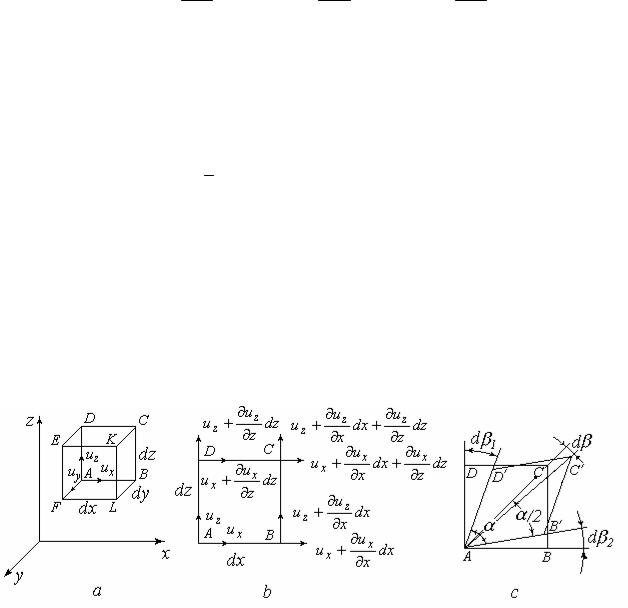
Выделим в жидкости неподвижный относительно координатных осей объем пространства в виде параллелепипеда со сторонами dx, dy, dz, через который протекает жидкость (рис. 3.4). Рассмотрим течение жидкости в направлении оси х. Скорость в центре грани ABCD равна ux , а в центре грани

A´B´C´D´ она равна ux ux dx, так как при перемещении от одной грани к

x

другой изменилась только координата x.

Масса жидкости, втекающей за время dt в выделенный объем через грань ABCD, равна: dM' dydz uxdt. Масса жидкости, вытекающей через грань

		ux
	A´B´C´D´ за то же время, равна: dM" dydz ux		dx dt.
		x

Следовательно, изменение массы внутри объема за счет разности скоростей в направлении оси x будет равно:

		"	'	ux
	Mx	dM x dM x dydz			dx dt.
				x

Записав аналогичные выражения для осей y и z, получим:

	My dxdz	uy	dy dt;	Mz dydx	uz	dz dt .
		y			z

Тaк как жидкость неразрывна и несжимаема, то масса внутри объема должна быть постоянной − сколько в него втекло, столько из него должно и вытечь. Следовательно, общая сумма изменения массы должна равняться нулю:

dxdydz ux dt dxdydz uy dt dxdydz uz dt 0.

x

y

z

После сокращения на величины, не равные нулю, получим:

u	x		uy		u	z	0.	(3.7)
			y
x					z

Это выражение называется дифференциальным уравнением неразрывности. Сумма частных производных от проекции вектора по координатам

называется дивергенцией (расхождением). Поэтому выражение (3.7) можно записать в виде: divu 0.

3.3. Теорема Коши – Гельмгольца

Скорость движения жидкой частицы складывается из скорости ее поступательного движения, скорости вращения относительно некоторой точки (полюса) и деформационной скорости.

Рассмотрим движение жидкой частицы в форме бесконечно малого куба со сторонами dx = dy = dz относительно системы координат (рис. 3.5, а).

Рис.3.5. К доказательству теоремы Коши − Гельмгольца

В точке А скорость жидкости имеет проекции ux, uy , uz . В точке К, где изменились все три координаты, uK uK (x dx,y dy,z dz ), или:

uKx ux

ux

dx

ux

dy

ux

dz;

(3.8)

x

y

z

uKy uy

uy

dx

uy

dy

uy

dz;

(3.9)

x

y

z

uKz uz

uz

dx

uz

dy

uz

dz.

(3.10)

x

y

z

Рассмотрим вначале скорость вдоль оси х. В правой части выражения (3.8) каждое из двух последних слагаемых разобьем на две половины; кроме

того, прибавим и отнимем

1

(

u

z

dz

uy

dy). Получим:

2

x

x

ux

ux

ux

ux

ux

uz

uKx ux

dx

1

dy

1

dy

1

dz

1

dz

1

dz

x

2 y

2 y

2 z

2 z

2 x

1

uy

1

u

z

1

uy

u

x

1

u

x

uy

dy

dz

dy u

x

dx

dy

2

x

2

x

2

x

x

2

y

x

1

u

x

uy

1 u

x

u

z

1

u

x

u

z

dy

dz

dz.

(3.11)

2

y

x

2

z

x

2

z

x

Возьмем грань АВСD и распишем проекции скорости в каждой точке этой грани (рис. 3.5, b). Обратимся к правой части выражения (3.11). Здесь ux − поступательная скорость точки А. Разность скоростей в точках А и В (а также в

точках С и D) в направлении оси х равна ux dx. Значит, ux dx − скорость

x x

линейной деформации грани в направлении оси х.

Ребро ВС вращается относительно точки В с линейной скоростью ux dz.

z

Угловую скорость вращения получим, разделив линейную скорость на радиус

	dz. Она равна	ux	. Угол поворота d 1			ux	dt . Такую же угловую скорость и
		z				z
	угол поворота имеет ребро AD . Ребро АВ вращается относительно точки А с
	угловой скоростью			uz	, а угол поворота равен d 2			uz	dt .
				x				x

Рассмотрим изменение формы грани АВСD (рис. 3.5, с). Она переходит в положение A´B´C´D´ . Этот переход можно разложить на два движения:

угловая деформация грани (за счет появления углов dβ1 и dβ2 прямой угол DAB становится равным α.);

поворот деформированной грани A´B´C´D´ как твердого тела относительно точки А, что можно судить по углу dβ поворота диагонали от начального положения.

o

o

d 1

d 2.

Из рисунка следует: d 45

(

d 2). Угол 90

2

90o

Поэтому d 45

o

d 1 d 2

d 2

d 1

d

2

d 2

d 1

d 2

2

2

1

u

u

2

2

x

z

dt.

(3.12)

z

x

2

Угловая скорость вращения диагонали относительно оси y равна:

	d	1		ux			uz
y								.
	dt				z		x
		2

Аналогично получим выражения для составляющих угловой скорости вокруг остальных двух осей. В итоге получим:

1

u

z

uy

x

;

(3.13)

2

y

z

1

ux

uz

y

;

(3.14)

z

x

2

1

uy

u

x

z

.

(3.15)

2

x

y

Удвоенный вектор угловой скорости называется вихрем: Общий угол перекашивания фигуры ABCD равен:

	ux			uz
	d y d 1 d 2				dt.
		z		x

2 .

(3.16)

Назовем скоростью угловой деформации γy грани относительно оси у (это скорость деформации двугранного угла с ребром, параллельным оси у)

	1			d y	1		ux			uz
величину y											.
				dt				z		x
	2				2

Проведя аналогичные выкладки для осей x и z , получим:

1

u

z

uy

x

;

(3.17)

2

y

z

1

ux

uz

y

;

(3.18)

z

x

2

1

uy

u

x

z

.

(3.19)

2

x

y

С учетом полученных выражений формулы (3.8), (3.9) и (3.10) примут вид:

uKx ux

ux

dx zdy ydz ydz zdy;

(3.20)

x

uKy uy

uy

dy xdz zdx zdx xdz;

(3.21)

y

uKz uz

uz

dz xdy ydx xdy ydx.

(3.22)

z

0. Следовательно:

При безвихревом течении x y z

u

z

uy

0;

u

x

u

z

0;

uy

u

x

0, или

(3.23)

y

z

z

x

x

y

u

z

uy

;

u

x

u

z

;

uy

u

x

.

(3.24)

y

z

z

x

x

y

Согласно математическому анализу, эти условия выполняются , если существует такая функция (x, y,z), для которой

ux		, uy		, uz		.	(3.25)
	x		y		z

Тогда, например, последнее из уравнений (3.24) будет выглядеть так:

											2			2
															0.	(3.26)
					y x					x y			y x
x		y

Функция φ называется потенциалом скорости, а безвихревое течение называется потенциальным.

Для потенциального движения уравнение неразрывности (3.7) может быть представлено с учетом зависимостей (3.25) в виде:

u

x

2

uy

2

u

z

2

;

;

.

x

x2

y

y

2

z

z2

Отсюда

2

2

2

0 .

(3.27)

x2

z2

y2

Полученное выражение называется уравнением Лапласа.

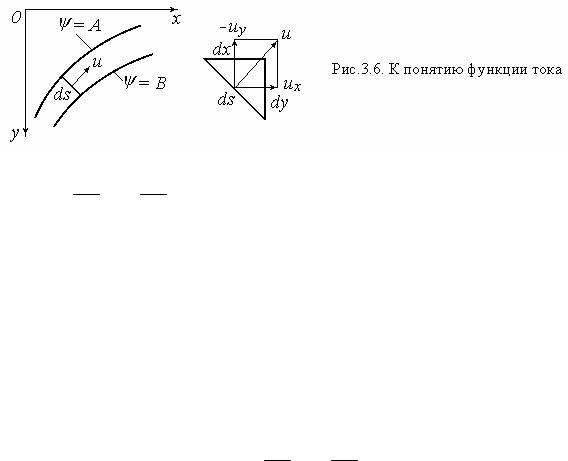
3.4. Функция тока

Рассмотрим плоское движение жидкости в координатах x, y (рис. 3.6). Уравнение линии тока (3.1) в этом случае имеет вид:

dx		dy	,	или uxdy uydx, или	uxdy uydx 0.	(3.28)
ux uy

Пусть имеется функция (x, y), непрерывная в плоскости координат и

удовлетворяющая условиям:		ux ;		uy.
	y		x

Тогда, подставив эти выражения в (3.28), получим:

dy dx d 0.y x

Следовательно, ψ = С.

Функция, сохраняющая постоянное значение на данной линии тока,

называется функцией тока.

Выявим физический смысл функции тока. Рассмотрим плоскую элементарную струйку толщиной в единицу длины. Тогда площадь живого сечения d ds 1 ds, где ds − расстояние между двумя линиями тока.

Рассмотрим в увеличенном виде элементарный объем треугольной формы (рис. 3.6, справа). Через поверхность, соответствующую линии ds, жидкость в него втекает, через поверхности, соответствующие отрезкам dx и dy, вытекает.

Расход втекающей жидкости должен равняться расходу вытекающей:

dQ uds uxdy uydx dx dy d .

x y

Таким образом, dQ d . Интегрируя, найдем:

	A
Q	dQ d A B.	(3.29)

d B

Здесь А и В – постоянные значения функции тока на линиях тока, ограничивающих рассматриваемую часть потока жидкости.

3.5. Примеры кинематического анализа движения жидкости

Кинематический анализ включает:

а) определение поля скоростей (проекций скорости на координатные оси); б) проверку удовлетворения уравнения неразрывности (что равноценно проверке возможности существования заданного течения жидкости; в) проверку условия потенциальности (безвихревого течения); г) нахождение уравнения линий тока.

Рассмотрим несколько простейших плоских течений в случае, когда задана функция тока.

1.Функция тока задана в виде: ay.

находим проекции скорости: ux

a;uy

0;

y

x

проверяем условие неразрывности:

u

x

uy

0 0 0;

y

x

проверяем условие потенциальности:

0;

2

0;

a;

2

0;

2

2

0;

x

x2

y2

x2

y2

y

C

находим уравнение линий тока по функции тока: ay C;

y

C .

a

1

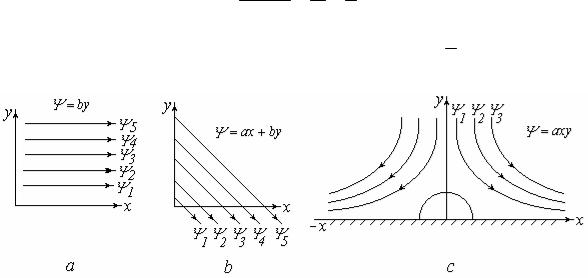
Получаем семейство прямых, параллельных оси x (рис. 3.6, а ).

2.Функция тока задана в виде: ax by.

находим проекции скорости: ux

b;uy

a;

y

x

проверяем условие неразрывности:

u

x

uy

0 0 0;

y

x

проверяем условие потенциальности:

a;

2

0;

b;

2

0;

2

2

0;

x

x2

y2

x2

y2

y

находим уравнение линий тока по функции тока:

ax by C ; y C ax C a x. b b b

Получаем семейство прямых с угловым коэффициентом a (рис. 3.6, b ). b

Рис.3.6. К кинематическому анализу течений

3.Функция тока задана в виде: axy.
находим проекции скорости: ux		ax;uy			ay;
	y			x