Rybleva_teoria veroatnosti_2014

4.11Каждое изделие с вероятностью 0,01 дефектно. Контроль может пропустить дефектное изделие с вероятностью 0,10, и забраковать годное с вероятностью 0,05. Определить:

а) вероятность приемки наудачу взятого изделия; б) процент годных изделий среди принятых.

4.12В начале года капитал фирмы составлял 1 млн.руб. Каждый месяц капитал равновероятно увеличивается или уменьшается на 200 тыс. руб. Найти риск разорения фирмы за полгода.

4.13Студент разыскивает нужную ему формулу в трех справочниках. Вероятность того, что формула содержится в 1, 2 и 3 справочнике соответственно равна 0,6; 0,7; 0,8. Найти вероятность того, что формула содержится:

а) только в одном справочнике; б) только в двух справочниках; в) во всех трех справочниках; г) хотя бы в одном справочнике; д) ни в одном справочнике.

4.14В районе 24 человека обучаются на заочном отделении университета, из них 6 – на юридическом факультете, 12 – на географическом и 6 – на экономическом. Вероятность успешно сдать все экзамены на предстоящей сессии для студентов юридического факультета равна 0,6, географического – 0,76 и экономического – 0,8. Найти вероятность того, что наудачу взятый студент, сдавший успешно все экзамены, окажется студентом экономического факультета.

4.15В трех параллельных группах была проведена одна и та же контрольная работа. В первой группе обучаются 30 студентов, во второй

– 28, в третьей – 27. Выполненных на «отлично» в первой группе оказалось 8 работ, во второй – 6, в третьей – 9. Найти вероятность того, что первая взятая наудачу при повторной проверке работа, из работ, принадлежащих группе, которая также выбрана наудачу, окажется

выполненной на «отлично».

51

4.16Дано P(A)=0,8; P(A∩B)=0,5; P(A/B)=0,9. Найти P(B), P(B/A), P(AUB)

и выяснить, зависимы ли события A и B .

4.17Вероятность попадания в цель равна 0,3, а вероятность ее уничтожения равна 0,05. Найти вероятность того, что при попадании в цель она будет уничтожена.

4.18В произвольном порядке выписываются две буквы И и две буквы С. Найти вероятность того, что обе буквы С стоят рядом, при условии, что последняя по порядку буква есть буква И.

4.19Из колоды в 36 карт берется наудачу одна карта. Зависимы ли события А – «выбран валет» и В – «выбрана карта черной масти»?

4.20Радист трижды вызывает корреспондента. Вероятность того, что будет принят первый вызов, равна 0,3, второй – 0,4, третий – 0,5. По условиям приема события, состоящие в том, что данный вызов будет услышан, независимы. Найти вероятность того, что корреспондент вообще услышит вызов.

4.21Монета бросается до первого появления герба. Какова вероятность того, что понадобится четное число бросков?

4.22Из букв А, А, И, Л, М, Н разрезной азбуки выбирают наудачу по одной и ставят в ряд. Найти вероятность того, что получится слово:

а) МИНА; б) НАЛИМ; в) МАЛИНА?

Ответы:

4.1 а) нет; б) нет; в) да.

4.2 Q/P. 4.3 а) 0,096;

б) 0,936. 4.4 0,98. 4.5

m

m 1

...

m 101

m

101

а) 0,6; б) 0,6. 4.6

;

. 4.7 0,991.

n 1

n 101

n

n

4.8 а) 0,1327; б) 0,2954.

4.9 а) 0,032; б) 0,316. 4.10 а) 0,5; б) 0,65. 4.11

а) 0,942; б) 0,998. 4.12

0,03125.

4.13 а) 0,188; б) 0,452; в) 0,336; г)

0,976; д) 0,024. 4.14 0,27. 4.15 19/70. 4.16 5/9; 5/8; 0,8(5). 4.17 1/6. 4.18 2/3. 4.19 нет. 4.20 0,79. 4.21 1/3 4.22 а) 1/180; б) 1/360; в) 1/360.

52

R(A,B)

1.5. Коэффициенты регрессии и корреляции случайных событий

Характер влияния одного случайного события на другое может быть различным, поэтому и степень такой зависимости будет разной.

Коэффициентом регрессии события A относительно события B называется разность между условной вероятностью события A при

условии B и условной вероятностью события A при условии B :

R(A,B) P(A / B) P(A / B) .

Коэффициент регрессии учитывает реализуемость

явления, описываемого событием A, как при условии, что явление, описываемое событием B, реализуется, так и при условии, что это явление не реализуется.

Утверждение 1. Коэффициент регрессии события A относительно события B можно вычислить по формуле:

R(A,B) P(AB) P(A)P(B) .

P(B)(1 - P(B))

Заметим, что коэффициент регрессии R(A,B) - несимметричен: он может быть не равен коэффициенту регрессии

R(B, A) P(B / A) - P(B/ A) P(AB) - P(A)P(B) ,

P(A)(1 - P(A))

измеряющему зависимость события B от события A.

Свойства коэффициента регрессии:

1)события A и B – независимы <=> R(A,B) 0 ;

2)R(A,B) ≤ 1;

3)R(A,B) 1 <=> P(A) P(B) P(AB) , т.е. событие A достоверно

при условии B и невозможно при B ;

4)R(A,B) -R(A, B) .

Используя коэффициенты регрессии, можно определить симметричную меру зависимости событий – коэффициент корреляции. Будем рассматривать случайные события A и B, удовлетворяющие следующим условиям:

53

P(A) 0 ; 1- P(A) P(A) 0 ; P(B) 0 ; 1- P(B) P( B) 0 .

В силу определения коэффициенты регрессии для событий A и B имеют одинаковые знаки: R(A,B)R(B, A) 0 .

Следовательно, для них можно определить среднее геометрическое: R(A,B)R(B, A) , выбирая знак перед корнем равным знаку коэффициентов регрессии R(A,B) и R(B, A) .

Коэффициентом корреляции событий A и B называется число

K(A,B) 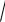R(A,B)R(B, A) .

Утверждение 2. Коэффициент корреляции событий A и B может быть

вычислен по формуле: K(A,B)			P(AB) - P(A)P(B)
					.
			P(A)(1 - P(A))P(B)( 1 - P(B))
Коэффициент корреляции может принимать значения от -1 до +1.
Если K(A,B) 0 , то говорят,	что события A и B – отрицательно

коррелированы, т.е. событие B уменьшает вероятность события A. Если K(A,B) 0 , то события A и B – положительно коррелированы:

P(A / B) P(A) .

Заметим, что из определения коэффициента корреляции следует его симметричность:K(A,B) K(B, A) .

Свойства коэффициента корреляции:

1)события A и B – независимы <=> K(A,B) 0 ;

2)K(A,B) 1;

3)K(A,B) 1 <=> P(A) P(B) P(AB) ;

4)K(A,B) -K(A, B) .

Пример 5.1 По данным переписи 1951 года, в Англии среди отцов, имеющих сыновей, оказалось 13% темноглазых и 87% светлоглазых. У темноглазых отцов оказалось 39% темноглазых и 61% светлоглазых сыновей. У светлоглазых отцов оказалось 10% темноглазых и 90% светлоглазых сыновей. Какова вероятность того, что выбранные наугад

54

среди этого населения отец и сын имеют глаза одинакового цвета? Какова зависимость между цветом глаз отца и сына?

Решение: Введем обозначения для рассматриваемых явлений: ОТ - отец темноглазый; Осв - отец светлоглазый;

СТ - сын темноглазый; Ссв - сын светлоглазый.

По условию известны вероятности:

P(OТ ) 0,13 ; P(Oсв ) 0,87 ; P(CT / OT ) 0,39 ; P(Cсв / ОТ ) 0,61; P(CT / Oсв ) 0,10 ; P(Cсв / Осв ) 0,90 .

Вероятность того, что сын и отец имеют глаза одинакового цвета равна:

P(ОТСТ ОсвСсв ) P(ОТ )P(СТ / ОТ ) P(Осв )P(Cсв / Осв )

0,13·0,39 0,87·0,90 0,8337 .

Для определения зависимости между цветом глаз отца и сына вычислим коэффициенты корреляции K(СТ ,ОТ ), K(Ссв ,Осв ) .

По формуле полной вероятности получаем:

P(CT ) P(OT )P(CT / OT ) P(Осв )P(CТ / Осв ) 0,13·0,39 0,87·0,10

0,1377 .

	Тогда K(CT ,OT )				P(CTOT ) - P(CT )·P(OT )
					P(CT )(1- P(CT ))P(OT )(1- P(OT ))
			0,13·0,39 - 0,1377·0,1 3				0,283 .
			0,1377·0,8 623·0,13·0 ,87
			Коэффициент		корреляции положительный, следовательно,

темный цвет глаз отца увеличивает вероятность того, что и у сына глаза будут темного цвета, но корреляция этих событий слабая.

Так как события Осв и Ссв - противоположны событиям ОТ и СТ ,

то К(СТ ,ОТ ) К(Ссв ,Осв ) -К(Ссв ,ОТ ) -К(СТ ,Осв ) .

■

Пример 5.2 Проверяется эффективность нового медицинского препарата. Из имеющихся 60 зараженных животных 30-ти вводится и 30-ти не вводится этот препарат. Среди животных, которым был введен

55

препарат, 29 выздоравливают и 1 – нет. Среди животных, которым не введен препарат, 26 выздоравливают и 4 – нет. Какова корреляция между введением препарата и выздоровлением?

Решение: Пусть П – событие, состоящее в том, что животному вводится

_ _

препарат; П - препарат не вводится; В - животное не выздоравливает; В

–

животное

выздоравливает.

По

условию

заданы вероятности:

P(П) 0,5; P(В / П) 29 / 30 ;

_

_

_

_ _

P(П ) 0,5 ;

P(В/ П) 1/ 30 ;

P(В / П) 26 / 30 ;

P(В/ П) 4 / 30 .

Тогда P(ВП ) P(П)P(В / П) 0,5·

29

29

;

30

60

По формуле полной вероятности:

_

_

29

26

55

P(В) P(П)P(В / П) P(П)P(В / П) 0,5·

0,5·

.

30

30

60

Следовательно, коэффициент корреляции равен:

K(В,П)

P(ВП ) - P( В )P(П)

29 / 60 - (55/60)·(1 /2)

P( В)(1- P( В ))P(П)(1 - P(П))

(55/60)·(5 /60)·(1/2) ·(1/2)

3

0,2.

5

11

Интерпретация полученного результата такова: введение препарата повышает шансы животного на выздоровление, но незначительно.

■

Пример 5.3 В Т-образный лабиринт запустили голодных мышек, из которых 50% бегут в левый конец и 50% - в правый. Среди мышек, побывавших в левом конце с пищей и вновь помещенных в лабиринт, (50+100·ε)% бегут опять налево, а (50-100·ε)% - направо. Среди мышек, побывавших в правом конце без пищи и вновь помещенных в лабиринт 50% бегут налево и 50% - направо.

1)Какова вероятность, что вновь помещенная в лабиринт мышка побежит в левый конец?

56

2)Какова условная вероятность того, что мышка бегала к пище в первый раз при условии, что она побежала к пище во второй раз?

3)Какова зависимость между получением пищи и поведением мышки при повторном помещении в лабиринт?

Решение: Обозначим через 1л - событие, состоящее в том, что мышка бегала в первый раз налево; 1пр - при первичном помещении мышки в лабиринт она побежала в правый конец; 2л - при повторном помещении в лабиринт мышь побежала в левый конец; 2пр - мышка побежала

направо во второй раз.

1) По условию при первичном помещении в лабиринт (когда мышь еще не знает, что ее ожидает в правом и в левом концах лабиринта) варианты «сходить налево» и «направо» - равновероятны:

P(1л ) 0,5 и P(1пр ) 0,5 .

При повторном помещении в лабиринт для тех мышей, которые первый раз бегали в правый конец и остались голодными, ситуация ничем не отличается от предыдущей:

P(2л / 1пр ) 0,5 и P(2пр / 1пр ) 0,5 .

Для мышей, сбегавших в первый раз налево и оставшихся довольными (сытыми), вероятности для второго забега изменятся:

P(2л / 1л ) 0,5 ε ; P(2пр / 1л ) 0,5 - ε .

Вероятность побежать при повторном помещении в лабиринт в левый конец с пищей по формуле полной вероятности равна:

P(2л ) P(1л )P(2л / 1л ) P(1пр )P(2л / 1пр ) 0,5(0,5 ε) 0,5·0,5

0,5·(0,5 ε 0,5) 0,5·(1 ε ) .

2) Апостериорная вероятность того, что мышь бегала к пище в первый раз при условии, что она побежала к пище во второй раз, вычисляется по формуле Байеса:

P(1 / 2л)	P(1л)P(2л / 1л )		0,5·(0,5 ε )		0,5 ε	.
л	P(2л )		0,5·(1 ε )		1 ε

57

3) Меру зависимости между получением пищи при первичном «забеге» и поведением мышки при повторном помещении в лабиринт определим с помощью коэффициента корреляции:

K(1л ,2

л )

P(1л ·2л ) - P(1л )·P(2 л )

0,5·(0,5 ε ) - 0,5·0,5·(1 ε )

P(1л )P(1пр )P(2л )P(2пр )

0,5·0,5·0,5·(1

ε )·0,5·(1 - ε )

0,5·ε

ε

.

0,5·

1 - ε2

1- ε2

Если ε=0,

то K(1л ,2л ) 0, т.е.

зависимости между получением

пищи в первый раз и поведением мышки при повторном помещении в лабиринт нет. Если ε ≠ 0, то K(1л ,2л ) 0, т.е. зависимость между получением пищи в первый раз и поведением мышки при повторном помещении в лабиринт есть.

Например, если ε=1/2, то K(1 ,2		)	1				1		0,577 .
	л
л			3				1,732

■

Задачи для самостоятельного решения:

5.1В продукции завода брак вследствие дефекта А составляет 6,1%, а вследствие дефекта В – 2,8%. Общий брак по одному из этих дефектов – 5,8% всей продукции завода. Какова корреляция между дефектами А и В?

5.2Статистика показывает, что среди двоен 32% оба близнеца мальчики и 28% - девочки. Какова корреляция пола близнецов?

5.3По линии связи посылаются сигналы 0 и 1. Проходя по линии связи, переданный сигнал может исказиться и превратиться в другой сигнал. Приемник улавливает сигнал, пришедший по линии связи. Таким образом, может быть принят не тот сигнал, который был передан. Известны вероятности:

P(1) 0,6 - вероятность того, что посылается сигнал 1;

P(0) 0,4- посылается сигнал 0;

58

P(1/ 1) 0,9- принят сигнал 1, при условии, что и послан был сигнал 1;

P(0 / 1) 0,1 - принят сигнал 0, а послан был сигнал 1;

P(1/ 0) 0,3 - принят сигнал 1, при условии, что отправлен был 0;

P(0 / 0) 0,7- принят сигнал 0 и отправлен сигнал 0.

Какова вероятность, что принимается сигнал 1? Какова корреляция между посланным и принятым сигналами?

Ответы:
5.1 K A,B 0,742 .	5.2	K A,B 0,2.	5.3	P A =0,66;
				1

K A1,B1 0,6 .

1.6. Модель повторных независимых испытаний: формула Бернулли и еѐ асимптотические приближения

На практике некоторые ситуации можно представить в виде многократно повторяющихся испытаний при данном комплексе условий, в которых представляет интерес оценить шансы числа k появлений некоторого события A в n испытаниях. Например, необходимо определить вероятность изготовления некачественных изделий в партии изделий, изготовленных на определенном оборудовании при постоянстве технологических и организационных условий; или определить вероятность определенного числа попаданий в мишень при нескольких выстрелах; или оценить шансы появления определенного числа гербов при неоднократном подбрасывании монеты.

Если вероятность наступления события A в каждом испытании не меняется в зависимости от исходов других, то такие испытания называются независимыми относительно события A. Если независимые повторные испытания проводятся при одном и том же комплексе условий, то вероятность наступления события A в

каждом испытании одна и та же. Описанная последовательность независимых испытаний называется схемой Бернулли.

59

Пусть производится n независимых опытов, в каждом из которых с одной и той же вероятностью p может наступить некоторое событие A. Требуется для заданного числа k найти вероятность следующего события: в n опытах событие A наступит ровно k раз. Если в результате испытаний событие A произошло k раз (неважно в каком порядке), то это означает, что совместно наступили k событий A и n-k событий A , вероятности которых в каждом отдельном опыте равны p и q соответственно. Так как все n событий независимы, то вероятность появления k раз события A в определенной последовательности равна pkqn-k . Однако событие A может появиться k раз в n опытах в совершенно другой последовательности:

AA...A AA...A

AA

A...AA ... AA...A AA...A.

k раз n-k раз

n-k раз k раз

Каждый вариант записывается в виде строки длиной n, в которой k

компонент – это события A и n-k компонент – события A . Число всех таких вариантов (слагаемых в указанной сумме) равно числу способов

выбора k элементов из n, т.е. числу сочетаний Cnk ; так как все эти варианты между собой несовместны, то искомая вероятность будет равна сумме вероятностей всех указанных несовместных событий, т.е.

произведению Cnk pkqn-k . Чтобы подчеркнуть зависимость полученного выражения от n и k, обозначим его через Pn k . Итак, вероятность появления события A в n независимых испытаниях ровно k раз равна:

	P	k Ck pkqn-k		n!		pkqn-k .
				k! n - k !
	n	n

Полученная формула называется формулой Бернулли.

Пример 6.1 Игральная кость подбрасывается 10 раз. Какова вероятность того, что «пятерка» выпадает при этом ровно 3 раза?

60