Kretov1

§ 2.1. ЗВНЪУр˚. гЛМВИМ˚В УФВр‡ˆЛЛ М‡‰ МЛПЛ. к‡БОУКВМЛВ ‚ВНЪУрУ‚

При сложении векторов их одноименные координаты складываются, при вычитании — вычитаются, при умножении вектора на число — умножаются на это число:

a ± b ={ x1 ± x2; y1 ± y2; z1 ± z2}; λ a = {λx1; λy1; λz1}.

Определение 18. Вектор r = OM , соединяющий начало координат с произвольной точкой М(x; y; z) пространства, называется радиусом-вектором точки М.

Координаты точки М — это координаты ее радиус-вектора r = {x; y; z}, или r = x i + y j + z k .

Если вектор AB задан точками А(x1; y1; z1) и В(x2; y2; z2), то его координаты аx, аy, аz вычисляются по формулам:

		ax = x2 – x1, ay = y2 –y1, az = z2 – z1:
				= {x2 –x1; y2 –y1; z2 – z1}.	(2.1.8)
			AB
Тогда
|		|= (x1 − x2 )2 +(y1 − y2 )2 +(z1 − z2 )2 .			(2.1.9)
	AB

бДСДзаь

267.Даны две точки А1(3; –4; 1) и А2(4; 6; – 3). Найти координаты вектора A1 A2 .

268.Даны три последовательные вершины параллелограмма: А(1; – 2; 3), В(3; 2; 1), С(6; 4; 4). Найти его четвертую вершину D.

269.Найти координаты вектора AB , если А(1; 3; 2) и В(5;

8; – 1).

270.Нормировать вектор a = 3 i + 4 j – 12 k .

271. Найти длину вектора a = 20 i + 30 j – 60 k и его направляющие косинусы.

51

ЙО‡‚‡ II. щОВПВМЪ˚ ‚ВНЪУрМУИ ‡О„В·р˚

272.В треугольнике АВС дано: AB = a , AC = b , точка

М— середина стороны ВС. Выразить вектор AM через век-

торы a и b .

273. Какому условию должны удовлетворять ненулевые векторы a и b , чтобы имело место соотношение

| a + b |= | a – b |?

274. Даны векторы a и b . Коллинеарны ли векторы

c= a – 2 3 b и d = – 3 a + 6b?

275.Найти орт вектора a = {6; – 2; –3}.

276.Найти орт вектора a = {3; 4; –12}.

277.Даны: | a |=13, |b |=19 и| a + b |=24. Вычислить| a – b |.

278.

Даны: | a |= 11,

|

b

|= 23 и | a –

b

|= 30. Определить

| a +

|.

b

Векторы a и b

перпендикулярны, причем | a | = 5 и

279.

|

|= 12. Определить | a +

| и | a –

|.

b

b

b

280.

Векторы a и

образуют угол φ= 60°, причем | a |= 5

b

и| b |= 8. Определить | a + b | и | a – b |.

281.Даны два вектора a = {3; –2; 6} и b = {– 2; –1; 0 }.

Определить проекции на координатные оси следующих векто-

ров: 1) a +

b

; 2) a –

b

;

3) 2 a ;

4) –1/2

b

;

5) 2 a + 3

b

;

6) 1/3 a –

.

b

282. Определить, при

каких значениях α,

β векторы

коллинеарны.

a = – 2 i

+ 3 j + βk и b = αi – 6 j + 2 k

283. Два вектора a = {2; –3; 6} и b = { – 1; 2; –2} прило-

жены к одной точке. Определить координаты вектора c , направленного по биссектрисе угла между векторами a и b , при условии, что | c |= 3 42 .

284. Векторы AB = {2; 6; –4} и AC = {4; 2; –2} совпадают со сторонами ∆ АВС. Определить координаты векторов, при-

52

§ 2.1. ЗВНЪУр˚. гЛМВИМ˚В УФВр‡ˆЛЛ М‡‰ МЛПЛ. к‡БОУКВМЛВ ‚ВНЪУрУ‚

ложенных к вершинам треугольника и совпадающих с его медианами АМ, BN, CP.

285.На плоскости даны два вектора p = {2; – 3}, q = {1; 2}. Найти разложение вектора a = {9; 4} по базису p , q .

286.На плоскости даны три вектора a = {3; – 2}, b = {– 2; 1} и c = {7; –4}. Определить разложение каждого из этих трех векторов, принимая в качестве базиса два других.

287.Даны три вектора a ={3; –1}, b ={1; –2}, c ={–1; 7}.

Определить разложение вектора p = a + b + c по базису a , b .

288. Принимая в качестве базиса векторы AB = b и

AC = c , совпадающие со сторонами треугольника АВС, определить разложение векторов, приложенных в вершинах треугольника и совпадающих с его медианами.

289. Даны три вектора p = {3; – 2; 1}, q = {– 1; 1; – 2}, r = {2; 1; – 3}. Найти разложение вектора c = {11; – 6; 5} по ба-

зису p , q , r .

290. Даны четыре вектора a = {2; 1; 0}, b = {1; – 1; 2},

c = {2; 2; – 1} и d = {3; 7; – 7}. Определить разложение каждого из этих четырех векторов, принимая в качестве базиса три остальных.

291.Найти координаты вектора a , если | a |= 3 и углы между вектором и координатными осями равны: α= β= γ.

292.Представить вектор d ={4; 12; –3} как линейную ком-

бинацию векторов a ={2; 3; 1}, b ={5; 7; 0}и c ={3; –2; 4}.

293.На оси Oy найти точку М, равноудаленную от точек А(1; – 4; 7) и В(5; 6; –5).

294.На оси Ox найти точку М, расстояние которой от точки А(3; – 3) равно 5.

295.Даны вершины треугольника А(3; –1; 5), В(4; 2; –5), С(–4; 0; 3). Найти длину медианы, проведенной из вершины А.

53

ЙО‡‚‡ II. щОВПВМЪ˚ ‚ВНЪУрМУИ ‡О„В·р˚

296.

Дано

разложение вектора

c

по базису i

, j , k :

c = 16 i

– 15

j

+ 12 k . Найти разложение по этому же базису

вектора

,

параллельного вектору

c

и противоположного с

d

ним направления, при условии | d |= 75.

297. Даны четыре точки A, B, C, D. Точки M и N — сере-

дины отрезков AC и BD. Доказать, что MN = ½( AD + CB ).

298. ABCDEF — правильный шестиугольник,							AB = p ,
	= q . Выразить через p и q векторы		,		,			,			,
BC		CD		DE		EF				FA

AC , AD , AE .

299. В равнобедренной трапеции OACB величина угла

BOA = 60°, | OB |= | BC |= | CA |= 2. Точки M и N — середины сторон BC и AC. Выразить векторы AC , OM , ON , MN , через m и n — единичные векторы направлений OA и OB .

300. Дано: AB = a + 2 b , BC = – 4 a – b , CD = – 5 a – 3 b .

Доказать, что ABCD — трапеция.

301. Найти сумму векторов, соединяющих центр правильного треугольника с его вершинами.

302. На плоскости Oxy построить векторы OA = a = 2 i , OB = b = 3 i + 3 j , OC = c = 2 i + 6 j . Разложить вектор c по векторам a и b .

303. Дан вектор c = 4 i + 7 j – 4 k . Найти вектор d , параллельный вектору c и противоположный с ним направления,

если | d |= 27.

304. Найти вектор x , коллинеарный вектору a = i –2 j –2 k , образующийсортом j острыйуголиимеющийдлину| x |=15.

305. Заданы векторы a =2 i +3 j , b =–3 j –2 k , c = i + j –

– k . Найти: 1) координаты орта a °; 2) координаты вектора

54

§ 2.1. ЗВНЪУр˚. гЛМВИМ˚В УФВр‡ˆЛЛ М‡‰ МЛПЛ. к‡БОУКВМЛВ ‚ВНЪУрУ‚

a – 1/2 b + c ; 3) разложение вектора a + b – 2 c по базису i , j , k ; 4) прj( a – b ).

306. Зная радиус-векторы r1 , r2 , r3 трех последовательных

вершин параллелограмма, найти радиус-вектор ее четвертой вершины.

307. Даны радиус-векторы вершин треугольника ABC:

rA = i + 2 j + 3 k , rB = 3 i + 2 j + k , rC = i + j + k . Показать,

что треугольник ABC равносторонний.

308.Радиус-вектор точки M составляет с осью Oy угол 60°,

ас осью Oz угол 45°; его длина | r |= 8. Найти координаты точ-

ки M, если ее абсцисса отрицательна.

309. Три вектора a , b , и c попарно перпендикулярны, а длины их соответственно равны 2, 3 и 6. Найти длину суммы

Sэтих векторов и направляющие косинусы вектора S .

310.Три силы F1 , F2 , F3 приложены к одной точке, имеют взаимоперпендикулярные направления. Найти величину их

равнодействующей

F

, если известны величины сил

F1

= 2,

F2 = 10, F3 = 11.

311. Найти равнодействующую силу

сил

и

R

F1

F2 , а

также углы α и β, составляемые силой R с силами

и

F1

F2 , ес-

ли |

|= 15, |

|= 10; угол между силами

и

равен 45°.

F

F

F

F

1

2

1

2

312.Найти направление и скорость ветра, являющегося результатом взаимного действия морского бриза, дующего со

скоростью 14 м/с на берег и ветра, дующего с берега на море со скоростью 9 м/с и под углом в 60° к береговой линии.

313.Даны три некомпланарных вектора a , b и c . При

каком значении λ векторы λa + b + c , a + λb + c , a + b + λc компланарны?

55

ЙО‡‚‡ II. щОВПВМЪ˚ ‚ВНЪУрМУИ ‡О„В·р˚

314.

Разложить вектор S = a +

b

+ c

по трем некомпланар-

ным векторам m = a +

– 2 c , n = a –

, p = 2

+ 3 c .

b

b

b

315.

В треугольнике ABC прямая AM является биссектри-

сой угла BAC, причем точка M лежит на стороне BC. Найти

, если

=

,

= c , |

|= 2, | c |= 1.

AM

AB

AC

b

b

316.

Найти вектор x , направленный по биссектрисе угла

между векторами a = 7 i

– 4

j

– 4 k и

b = – 2 i

–

j

+ 2 k , если

| x |= 5

6 . Указание: x = λ(

° + a °).

b

317.

Какому условию удовлетворяют векторы a и

, если

b

1) | a +

|> | a –

|;

2) | a +

|< | a –

|;

3) | a +

|= | a |+ |

|;

b

b

b

b

b

b

4) | a +

|= | a |– |

|?

b

b

318.

В разложении вектора c = λ1 a + λ2

по двум неколли-

b

неарным векторам a и b могут ли оба коэффициента λ1 и λ2 или один из них равняться нулю?

319. Могут ли векторы a = {– 2; 1; –2}, b = {– 2; –4; 4}, c = {4; 3; –2} быть сторонами треугольника?

320. Коллинеарны ли векторы a и b , если коллинеарны

векторы a + b и a – b ?

321. Может ли вектор составлять с координатными осями углы 30°, 120°, 60°?

§ 2.2. лН‡ОflрМУВ ФрУЛБ‚В‰ВМЛВ ‚ВНЪУрУ‚

Определение 1. Скалярным произведением двух ненулевых

векторов a и b называется число, равное произведению длин этих векторов на косинус угла φ между ними.

Обозначение: a b . Таким образом,

a

b

=| a ||

b

|cos φ,

(2.2.1)

если a = 0 или b = 0, то a b = 0.

56

§ 2.2. лН‡ОflрМУВ ФрУЛБ‚В‰ВМЛВ ‚ВНЪУрУ‚

Формулу (2.2.1) можно записать в виде

a

= | a |прa

или a

= |b|пр

a .

(2.2.2)

b

b

b

b

Свойства скалярного произведения:

а) a

=

a ;

b

b

б) a (

+ c ) = a

+ a c ;

b

b

в) (λa )

= λ( a

);

b

b

г) a 2 = | a |2;

д) a

= 0 Ù a

(или a = 0, или

= 0).

b

b

b

Если векторы

a

и

заданы

своими

координатами

b

a = {x1; y1; z1},

= {x2; y2; z2}, то

b

a

= x1x2 +y1y2 + z1z2,

(2.2.3)

b

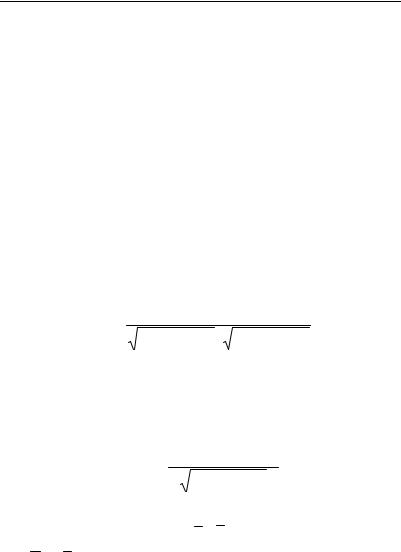
x1x2 + y1 y2 + z1z2

cos φ=

x2 + y2

+ z2

x2 + y2 + z2 ,

(2.2.4)

1

1

1

2

2

2

a

Ù x1x2 +y1y2 + z1z2 = 0,

(2.2.5)

b

a ||

Ù

x1

=

y1

=

z1

,

(2.2.6)

b

x2

y2

z2

пр

a = x1x2 + y1 y2 + z1z2 .

(2.2.7)

b

x22 + y22 + z22

Работа постоянной силы определяется по формуле:

A= F S , (2.2.8)

где F и S соответственно векторы силы и перемещения.

57

ЙО‡‚‡ II. щОВПВМЪ˚ ‚ВНЪУрМУИ ‡О„В·р˚

бДСДзаь

322.Найти скалярное произведение векторов a =3i +4 j +7 k

иb = 2 i – 5 j + 2 k .

323.

Даны векторы a = m i

+ 3 j + 4 k

и b = 4 i + m j – 7 k .

При каком значении m эти векторы перпендикулярны?

324.

Найти (5 a + 3 b

)(2 a –

b

), если | a |= 2, |

b

|= 3, a

b

.

325.

Определить угол между векторами a = i

+ 2 j + 3 k

и

b

= 6 i

+ 4 j – 2 k .

326.

Найти скалярное произведение

векторов 3 a – 2

и

b

5 a – 6

b

, если | a |= 4, |

b

|= 6 и ( a ,

b

) = π/3.

327.

+ 4

и

Определить угол между векторами a = 3 i

j

+ 5 k

b = 4 i + 5 j – 3 k .

328. При каком значении m векторы a = m i + j и b = 3 i –

3j + 4 k перпендикулярны?

329.Найти скалярное произведение векторов 2 a + 3 b + 4 c

и 5 a + 6			b	+ 7 c , если | a |= 1, |	b	|= 2, |c|= 3, а( a ,		b	) =( a , c ) =
=(	b	, c ) = π/3.

330. Найти работу силы F на перемещении S , если | F |=2,

| S |= 5, φ= ( F , S ) = π/6.

331. Найти единичный вектор, перпендикулярный векто-

рам a = i + j + 2 k и b = 2 i + j + k .

332. Даны векторы a = 2 i + 2 j + k и b = 6 i + 3 j + 2 k .

Найти прa b и прb a .

58

§ 2.2. лН‡ОflрМУВ ФрУЛБ‚В‰ВМЛВ ‚ВНЪУрУ‚

333. Определить угол между векторами a = – i + j и b = i –

– 2 j + 2 k .

334. Определить углы ∆ АВС с вершинами А(2; – 1; 3),

В(1; 1; 1) и С(0; 0; 5).

335. Даны точки А(а; 0; 0;), В(0; 0; 2а) и С(а; 0; а). Постро-

ить векторы OC и AB и найти угол между ними.

336.На плоскости дан треугольник с вершинами О(0; 0), А(2а; 0) и В(а; – а). Найти угол, образованный стороной ОВ и медианой ОМ этого треугольника.

337.Найти угол между биссектрисами углов хОу и yOz.

338.Из вершины квадрата проведены прямые, делящие противоположные стороны пополам. Найти угол между этими прямыми.

339.Найти угол между диагоналями параллелограмма, по-

строенного на векторах a = 2 i + j и b = – 2 j + k .

340.

Даны векторы a = i

+

j

+ 2 k и b = i

–

j

+ 4 k . Опреде-

лить пр

a и прa

.

b

b

341.

Определить длины диагоналей параллелограмма, по-

строенного навекторах a =2 m + n и b = m –2 n , где m и n —

единичные векторы, угол между которыми 60˚.
342. Дан вектор a = 2 m – n , где m и n		— единичные
векторы	с углом 120° между ними. Найти
		cos ( a , m ) и
	n ).
cos( a ,

343.Из вершины прямоугольника со сторонами 6 и 4 см проведены прямые, делящие противоположные стороны пополам. Найти угол φ между ними.

344.Даны три последовательные вершины параллелограм-

ма: А(– 3; –2; 0), В(3; – 3; 1) и С(5; 0; 2). Найти его четвертую

вершину D и угол между векторами AC и BD .

59

ЙО‡‚‡ II. щОВПВМЪ˚ ‚ВНЪУрМУИ ‡О„В·р˚

345.Даны точки A(3; 3; – 2), B(0; – 3; 4), C(0; – 3; 0). По-

строить векторы AB = a и CD = b и найти прa b .

346.Найти угол между векторами a =2 m +4 n и b = m – n , где m и n — единичные векторы, образующие угол 120°.

347. Даны

векторы OA = a и OB =

b

, причем | a |= 2,

|

b

|= 4, а ( a ,

b

) = 60°. Определить угол между медианой

OM

треугольника АОВ и стороной OA .

348. На осях Ox, Oy и Oz отложить равные отрезки | a |= 4 и на них построить куб. Пусть M — центр верхней грани, а N —

центр правой боковой грани куба. Определить векторы OM и

ON и угол между ними.

349.Даны единичные векторы a , b и c , удовлетворяющие условию a + b + c = 0. Вычислить a b + b c + c a .

350.Даны три вектора a , b и c , удовлетворяющие усло-

вию a + b + c = 0. Зная, что | a |= 3, | b |= 1 и | c |= 4, вычислить

ab + b c + c a .

351.Дано, что | a |= 3, | b |= 5. Определить, при каком зна-

чении α векторы a + αb , a – αb будут взаимно перпендикулярны.

352. Доказать, что вектор p = b ( a c ) – c ( a b ) перпендикулярен к вектору a .

353.Какому условию должны удовлетворять векторы a и b , чтобы вектор a + b был перпендикулярен к вектору a – b .

354.Вычислить, какуюработупроизводитсила f ={3; –2; –5},

когда ее точка приложения, двигаясь прямолинейно, перемещается из положения A(2; – 3; 5) в положение B(3; –2; –1).

355. Даны три силы M = {3; –4; 2}, N = {2; 3; – 5} и

P = {3; – 2; 4}, приложенные к одной точке. Вычислить, какую работу производит равнодействующая этих сил, когда ее точка

60