Численные методы / Лекции / Тема 2. Элементы теории погрешности

Тема 2. ЭЛЕМЕНТЫ ТЕОРИИ ПОГРЕШНОСТЕЙ Вычислительная погрешность

Можно выделить три основные причины возникновения погрешности при решении задачи численными методами.

1)Погрешность исходных данных – это неустранимая погрешность.

2)Погрешность дискретизации – это погрешность метода. Например, заме-

няя производную выражением u u(x x) , допускается погрешность дискре-

x

тизации, имеющая при х 0 порядок х.

3) Погрешность, связанная с конечной разрядностью чисел, представляемых в ЭВМ – это ошибка округления, она может нарастать в процессе вычислений.

Таким образом, основное требование, предъявляемое к вычислительному алгоритму, – это требование точности. Оно означает, что вычислительный алгоритм должен давать решение задачи с заданной точностью >0 за конечное число действий Q( ). Алгоритм должен быть реализуем, т.е. давать решение за допустимое машинное время.

Теория приближённых вычислений позволяет:

1.Зная степень точности данных (чисел), оценить степень точности результатов вычислений.

2.Брать данные с надлежащей степенью точности, достаточной для обеспечения требуемой точности результата.

3.Рационализировать процесс вычисления, освободив его от тех выкладок, которые окажут влияние на точность результата.

Погрешностью вычислений называется отклонение результата вычисления от истинного значения числа.

Абсолютная погрешность величины – разность между истинным х и при-

ближённым значениями х* этой величины.

= |х – х*|.

(2.1)

может быть положительной и отрицательной. Измеряется в тех же единицах измерения, что и сама величина (Пример 2.1).

Относительная погрешность величины – отношение абсолютной погреш-

ности к самой величине (Пример 2.2):

			[оотн.ед]				100% [%]	(2.2)
		х			х
	С точностью относительная погрешность связана следующим соотноше-
	нием:
			Т	1		.		(2.3)

Абсолютные и относительные погрешности числа принято округлять только в большую сторону, так как при округлениях границы неопределенности числа, как правило, увеличиваются. По этой причине вычисления ведутся с од- ним-двумя запасными знаками.

Значащие и верные цифры числа

Результат всякого вычисления выражается числом. Чтобы по самому начертанию числа можно было судить о точности, необходимо писать число так, чтобы в нём все значащие цифры, кроме последней, были верны и лишь последняя цифра была бы сомнительна и притом не более, как на единицу.

Значащими цифрами числа называют все его цифры, начиная с отличной от нуля первой слева, кроме нулей, стоящих в конце записи числа на месте отброшенных при округлении цифр.

Значащая цифра числа называется верной, если абсолютная погрешность числа не превосходит половины единицы того разряда, в котором она находится.

Если граница абсолютной погрешности приближённого числа равна половине единицы разряда последней его цифры, то все цифры этого числа называют точными. Если эта граница больше половины единицы разряда последней цифры числа, то последняя цифра такого числа называется сомнительной (При-

мер 2.3).

Обратим внимание на способ написания больших чисел, например, если в числе 12732000 четвёртая цифра уже сомнительна, то это число следует писать

так: 1,273 107 ; если бы была сомнительна пятая цифра, то это число написали

бы так: 1,2732 107 .

Точно также в целых числах, если в числе 37 ошибка начинается лишь с пятого знака, то это число следует писать так: 37,000.

Прямая задача теории погрешностей

Пусть в некоторой области G n-мерного числового пространства рассматривается непрерывно дифференцируемая функция y=f(x1, x2, …, xn). И пусть в точке (x1, x2, …, xn) области G нужно вычислить значение функции y=f(x1, x2, …,

xn).

Предположим, что нам известны лишь приближенные значения x1, x2, …, xn, x1* , x2* ,..., xn* G и их погрешности.

Вычислим приближенное значение y*=f( x1* , x2* ,...,xn* ). и оценим его абсо-

лютную погрешность.

Если воспользоваться формулой Лагранжа, то получим

	n
	y*=|у –y*| xi*		f (x1* ,...,xn* )	.	(2.4)
		x*
	i 1
		i

Абсолютная погрешность дифференцируемой функции одного аргумента y=f(x), вызываемая достаточно малой погрешностью аргумента х*, оценивается величиной

y*

f (x* )

x* .

(2.5)

Погрешность суммы. Пусть даны числа: х1, х2, …, хn и их относительные погрешности: 1, 2, …, n.

Абсолютная погрешность суммы чисел равна сумме абсолютных погрешностей слагаемых.

Относительная погрешность суммы этих чисел заключается между наибольшей и наименьшей из относительных погрешностей слагаемых. То есть она не превышает наибольшей из относительных погрешностей слагаемых.

				1		2 ... n .			(2.6)
				x1		x2 ... xn
С другой стороны имеем равенства:
	1	1		,	2	2 , ...,	n	n ,	(27)
		x1				x2		xn

а так как все дроби (2.6) рассматриваются лишь по их численной величине, то дробь (2.6), представляющая отношение суммы числителей к сумме знаменателей, заключается между наибольшей и наименьшей из дробей (2.7).

Поэтому, в том случае, когда все слагаемые приблизительно одинаковой величины (отношение наибольшего из них к наименьшему менее 10), надо их писать с одним и тем же числом знаков, столько же верных знаков будет и в сумме. (Пример 2.4)

Если числа сильно разнятся по величине, то разрядность их уравнивают по разрядности наибольшего из чисел. Однако в этом случае необходимо иметь информацию о том, как получены эти значения и не является ли число, резко отличающееся от остальных, например, «грубым выбросом», ошибочным значением и т.д. Тогда ориентироваться на него надо осторожно или вовсе этого не делать.

При сложении приближённых чисел абсолютная погрешность может быть как положительной, так и отрицательной, при этом может происходить взаимная компенсация погрешностей.

Погрешность произведения. Относительная погрешность произведения чисел равна сумме относительных погрешностей слагаемых.

Пусть множители х1, х2 имеют относительные погрешности 1, 2. Следо-

вательно, истинные величины этих чисел можно представить:
х1 = х1 (1 + 1) и х2 = х2 (1 + 2).	(2.8)
Истинная величина произведения будет:
х1х2 = х1х2 (1 + 1)(1 + 2) = х1х2(1 + ( 1 + 2) + 1 2).	(2.9)

Обыкновенно 1 и 2 весьма малы, например, 0,001; тогда произведение1 2 будет весьма мало по сравнению с их суммой и этим произведением можно

пренебречь. Тогда имеем:
х1х2 = х1х2(1 + ( 1 + 2)) = х1х2 +	х1х2( 1 + 2),	(2.10)

что подтверждает высказанное свойство для случая двух множителей, которое распространяется и на любое их количество. (Пример 2.5).

Деление. Так как деление на число х равносильно умножению на число 1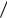 х

, то при делении относительная погрешность частного равна сумме относительных погрешностей делимого и делителя. Этой величины она достигает при условии, когда абсолютные погрешности делимого и делителя разных знаков. (Пример 2.6)

Возведение в степень. Относительная погрешность m-ой степени числа равна m-кратной относительной погрешности этого числа. Относительная погрешность квадрата числа равна удвоенной относительной погрешности числа, куба – утроенной и т.д. Относительная погрешность корня m-ой степени числа составляет 1/m часть относительной погрешности числа.

То есть это справедливо и для дробных степеней:

хP хP (1		)P хP (1 P			P(P 1)	2	...),	(2.11)
			1
1	1	1			1 2	1

где Р – степень числа.

Поскольку мала, то всеми членами, её содержащими, можно пренебречь, тогда:

хР хР (1 Р ) хР Р хР .			(2.12)
1	1	1

Вычитание. Относительная погрешность разности не поддаётся простому учёту. Особенно неблагоприятна в этом смысле разность двух близких по величине чисел.

Например, пусть даны числа 52,287 и 51,939. Разность между ними равна 0,348. Как известно, в каждом из исходных чисел можно ручаться только за первые четыре цифры, а так как в последней погрешность не более 1, то относитель-

ная погрешность самих чисел не более 150000 . Между тем, как в разности этих чисел 0,348 последняя цифра может быть неверна уже на две единицы и относи-

тельная погрешность может составить 2 0,348 , т.е. примерно в триста раз боль-

шую величину, нежели в данных. (Пример 2.7)

Относительная погрешность разности во столько же раз больше относительной погрешности в слагаемых, во сколько раз сама разность меньше каждого из них.

Выводы по теме 2

1.О точности результата судят по его относительной погрешности.

2.Точность вычисления нужно сообразовывать с точностью данных, а точность данных – с практической потребностью, для которой результат вычисления нужен.

3.При вычислении избегать вписывания лишних знаков, это не прибавит точности вычисления.

4.При сложении и вычитании приближённых чисел в результате следует сохранять столько десятичных знаков, сколько их в числе с наименьшим количеством знаков.

5.При умножении и делении приближённых чисел в результате надо оставлять столько значащих цифр, сколько их в данном числе с наименьшим количеством значащих цифр.

6.При возведении приближённых чисел в степень в результате сохраняется столько значащих цифр, сколько их в основании.

7.В промежуточных результатах можно брать одной цифрой больше, чем рекомендуют общие правила.

8.Если некоторые числа имеют больше десятичных знаков или значащих цифр, чем другие, то их предварительно следует округлить.

9.Логарифмами пользоваться с тем же количеством знаков, сколько их в чис-

лах.

10.Малые разности стараться вычислять непосредственно, не вычисляя самих чисел.

Контрольные вопросы по теме 2

1.Какая цифра числа называется значимой?

2.Какая цифра числа называется верной?

3.В чем заключается прямая задача теории погрешностей?

4.Как изменится оценка абсолютной погрешности суммы при увеличении числа слагаемых?

5.Как изменится относительная погрешность произведения при увеличении числа множителей?

Задания по теме 2

1. Округляя следующие числа до трех значащих цифр, определить абсолютную и относительную погрешности полученных приближенных чисел:

1.	8,2564	2.	0,26352
3.	0,02041	4.	0,7545
5.	1,335	6.	0,004912
7.	–0,0017392	8.	925,55
9.	–893,65	10.	74,525

2. Определить абсолютную погрешность следующих приближенных чисел

по их относительным погрешностям:
1.	а=23268, =0,1 %	2.	а=0,268,	=1 %
3.	а=3,52, =0,8 %	4.	а=12345,	=2 %

5.а=68,33, =1 % 6. а=0,00235, =1,5 %

3.Определить количество верных цифр в числе х, если известна его абсолютная погрешность:

1.	х=0,3941,	х =0,25 10–2	2.	х=14,00231, х =0,2 10–3
3.	х=0,1132,	х =0,1 10–3	4.	х=0,0842,	х =0,15 10–2
5.	х=38,2543, х =0,27 10–2		6.	х=0,00381,	х =0,1 10–4
7.	х=293,481, х =0,1		8.	х=–32,285,	х =0,2 10–2
9.	х=2,325,	х =0,1 10–1	10.	х=–0,2113,	х =0,5 10–2
4. Определить количество верных цифр в числе х, если известна его относи-
тельная погрешность:
1.	а=1,8921,	а=0,1 10–2	2.	а=9,3598,	а=0,1 %
3.	а=0,2218,	а=0,2 10–1	4.	а=0,11452,	а=10 %
5.	а=2,351,	а=0,1	6.	а=48361,	а=1 %
7.	а=0,02425,	а=0,5 10–2	8.	а=592,8,	а=2 %
9.	а=0,000135, а=0,15		10.	а=14,9360,	а=1 %

5.	Найти суммы приближенных чисел и указать их погрешности (все знаки
чисел верные):
	а) 1,145+421+88,2;	г) х1 + х2 + х3;
	б) 0,401+283,1+12,58;	х1=289,6; х1=0,2;
	в) 498,5 – 82,28+0,55567;	х2=34,44,6; х2=0,12;
		х3=209,55; х3=0,18.
6.	Найти произведение приближенных чисел и указать их погрешности (в
исходных числах все знаки верные):
	а) 4,59 9,5	г) 0,343 654 92,6
	б) 35,1 2,852	д) 2,67 9,1 2,283
	в) 0,03 17,6	е) 492,66 8346 0,0052
7.	Найти частное приближенных чисел:
	а) 5,684 5,032	г) 726,676 829
	б) 0,144 1,2	д) 754,9367 36,5
	в) 216 4,2	е) 7,3 4491
8.	Стороны прямоугольника равны а=5,03 0,02 м, b=5.89 0,02 м. Вычис-

лить площадь прямоугольника, а также абсолютную и относительную погрешность полученного результата.