МУ ТМ_2015 / Статика Тема5 строит. спец. (Михайленко, Живаго)

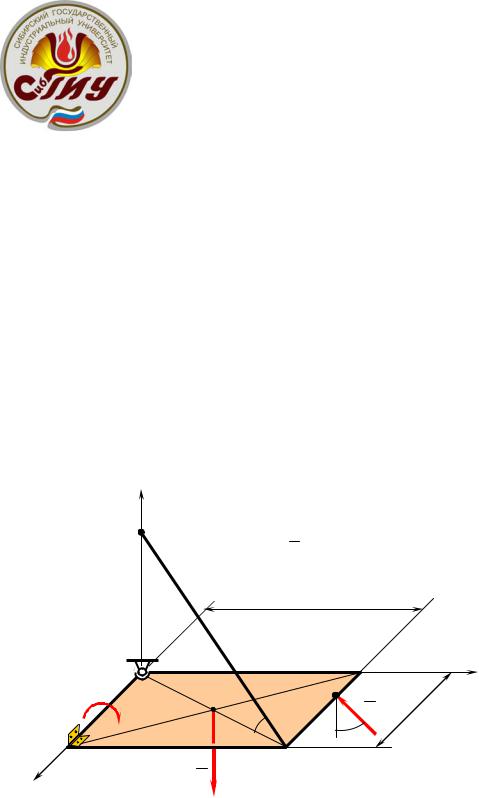
Институт машиностроения и транспорта

Кафедра теоретической механики

СТАТИКА

Практикум

Тема 5. РАВНОВЕСИЕ ПРОСТРАНСТВЕННОЙ ПРОИЗВОЛЬНОЙ СИСТЕМЫ СИЛ

Для студентов строительных специальностей

z

	K	F Ax
		b
	А		D	у
		E
M			F	а
	α	β
В		C
х	G

Новокузнецк

2012

Министерство образования и науки РФ

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования “Сибирский государственный индустриальный университет”

Кафедра теоретической механики

СТАТИКА

Тема 5. РАВНОВЕСИЕ ПРОСТРАНСТВЕННОЙ ПРОИЗВОЛЬНОЙ СИСТЕМЫ СИЛ

Практикум для выполнения самостоятельной работы

по дисциплине “Теоретическая механика”

Для студентов строительных специальностей

Новокузнецк, 2012

УДК 531 (075) С 78

Рецензент:

Доктор технических наук, профессор, заведующий кафедрой сопротивления материалов и строительной механики СибГИУ А.Г. Никитин

С 78 Статика: Практикум. / Сиб. гос. индустр. ун-т; сост: Н.И. Михайленко, Э.Я. Живаго. – Новокузнецк, Изд. центр СибГИУ, 2012. – 36 с.

Изложены методические указания для выполнения расчетнографических работ по дисциплине “Теоретическая механика”, раздел “Статика”, излагается краткая теория, приведены варианты заданий и ответы к ним.

Тема 5. РАВНОВЕСИЕ ПРОСТРАНСТВЕННОЙ ПРОИЗВОЛЬНОЙ СИСТЕМЫ СИЛ

Систему сил называют произвольной пространственной, если линии действия всех сил расположены произвольно в пространстве, т.е. не лежат в одной плоскости, не параллельны и не пересекаются в одной точке.

Любая произвольная система сил при приведении её к произвольному центру, приводится к одной силе, равной главному вектору, и паре сил, момент которой равен главному моменту

		n					n
	R	O* = ∑	Fk ,			M	O* = ∑mо (	Fk ) .
		k =1					k=1

Для равновесия произвольной системы сил, необходимо и достаточно, чтобы главный вектор и главный момент равнялись нулю

		n					n
	R	O* = ∑	Fk = 0,		M	O*	= ∑mо (	Fk ) = 0 .
		k =1					k =1

Записываются аналитические условия равновесия произвольной пространственной системы сил:

n			n	n
∑ X k = 0,			∑Yk = 0,	∑ Zk = 0,
k =1			k =1	k =1
n			n			n
∑m x (	Fk ) = 0, ∑m у (Fk					) = 0, ∑mz (	Fk ) = 0.
k =1			k =1			k =1

Для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы суммы проекций всех сил, приложенных к твердому телу, на оси декартовой системы координат, и алгебраические суммы моментов всех сил, относительно этих же осей, равнялись нулю.

Моментом силы F относительно оси называют алгебраический момент проекции этой силы на плоскость П, перпендикулярную оси, относительно точки пересечения оси с этой плоскостью.

1. Для нахождения значения момента силы относительно оси следует спроецировать силу на плоскость, перпендикулярную оси, и найти алгебраическое значение момента полученной проекции силы относительно точки пересечения оси с плоскостью (рисунок 1).

Mz (F ) = ±mO (Fп) = ±Fпh .

Момент силы относительно оси считается положительным, если с положительного направления оси видно стремление силы Fп повернуть тело или плоскость против хода часовой стрелки, и отрицательным – по ходу часовой стрелки. Здесь Fп – проекция вектора силы F на плоскость, перпендикулярную оси Oz.

z

F

h О

FП

П

Рисунок 1 – Момент силы относительно оси

Момент силы относительно оси равен нулю, если

•линия действия силы пересекает ось (h = 0);

•сила параллельна оси (FП = 0).

2. Вычисление моментов силы относительно осей существенно упрощается, если применить теорему Вариньона о моменте равнодействующей: разложить силу на составляющие, параллельные осям координат и записать алгебраические суммы моментов относительно выбранных осей.

Для равновесия пространственной системы параллельных сил необходимо и достаточно, чтобы сумма проекций всех сил на одну

из координатных осей, параллельную силам, и алгебраическая сумма моментов этих сил относительно двух других осей, равнялись нулю.

n	n			n
∑ Zk = 0	, то ∑m x (	Fk ) = 0,		∑m у (	Fk ) = 0 .
k=1	k=1			k=1

Контрольные задания

Однородная прямоугольная плита силой тяжести G закреплена в точке С невесомым стержнем или канатом, перекинутым через блок

D, на конце которого подвешен груз Q. На плиту действуют сила F и пара сил с моментом М. Плоскость действия пары сил указана в примечании. Определить реакции связей.

Примечание – номер варианта выбирается по сумме двух последних

цифр шифра.

Методические указания

Для решения задачи необходимо изучить следующие вопросы:

1.Основные виды связей, их реакции (шаровой шарнир, подпятник, подшипник).

2.Момент силы относительно оси и частные случаи его определения.

3.Теорема Вариньона о моменте равнодействующей системы

сил.

4.Условия равновесия произвольной пространственной системы сил и, как частный случай, системы параллельных сил в пространстве.

При решении задач на равновесие системы сил целесообразно придерживаться следующей последовательности:

•Выделить тело, равновесие которого следует рассмотреть.

•Показать на рисунке все активные силы, действующие на

тело.

•Определить, в каких точках, и какими связями закреплено тело. Применяя принцип освобождаемости от связей показать на рисунке реакции.

•Написать условия равновесия для пространственной системы сил и составить уравнения равновесия.

•Вычислить значения реакций. Если величина какой-либо реакции или её составляющей окажется отрицательной, то это означает, что направление этой силы противоположно тому, которое было принято первоначально.

•Написать ответ, указав, правильно или неправильно выбраны первоначальные направления реакций или их составляющих.

Пример выполнения и оформления задачи

Задача 1. Однородная прямоугольная плита силой тяжести G удерживается в горизонтальном положении шаровым шарниром в

точке А, цилиндрическим шарниром в точке В и канатом СK, натянутым под углом α к плите. В точке Е на плите плиту действует сила F , расположенная в плоскости, параллельная координатной плоскости Azy и составляющая угол β с прямой, параллельной оси Аz. На плиту в этой же плоскости действует пара сил с моментом М, стремящаяся повернуть плиту вокруг стороны АВ. Определить реакции связей, если АВ = DС = а, АD = ВС = b (рисунок 2).

Исходные данные: G = 10 кН, F = 5 кН, М = 20 кН м, а = 2 м,

b = 2 3 м, α = 45º, β = 60º, СЕ =		2а	м.
Определить: RA , RB , RC .		3
	z
	K		F Ax
			b
	А			D	у
			E
	M			F	а
		α	β
	В		C
х	G

Рисунок 2 – Схема задачи

Р Е Ш Е Н И Е

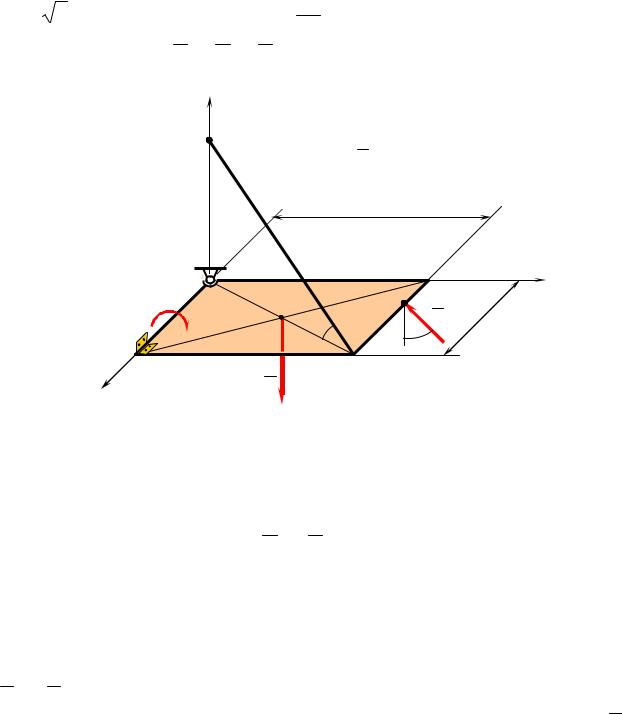
Рассмотрим равновесие плиты АBCD. Плита находится под действием активных сил G , F и пары сил с моментом М. Изображаем плиту без связей, а действие связей заменяем реакциями (рисунок 3).

Плита закреплена в точке А шаровым шарниром, направление реакции которого неизвестно. Представим реакцию тремя составляющими, параллельными выбранным осям координат X A ,

YA , ZA . Реакция неподвижного цилиндрического шарнира также неизвестна по направлению, её представляем составляющими YВ,

ZВ. В точке С гибкая связь – канат СK. Реакция каната направлена вдоль каната от плиты к стене. Реакцию RC спроецируем на ось Az и плоскость Аху, и представим ее в виде трех составляющих RCx , RCy

и RCz .

z

K

z1

b

A

Z

А

Y

A

R

С

RСz

D

у

X

A

R

E

ϕ

F

Сху

y а

Z

B

M

α

R

Сx

β

F

В

Fz

YB х1

C

х

RСу

G

Рисунок 3 – Равновесие плиты АBCD

	RCxy = RC cosα,
	RCx = −RCxy cosϕ = −RC cosα cosϕ,	(1)
	RCу = −RCxy sinϕ = −RC cosα sinϕ,
	RCz = RC sinα.

Из треугольника АВС определяем значение угла ϕ:

cosϕ =			AB	=	a	=	1	,
			AC		a2 + b2		2
ϕ = arccos	1	=	π = 60°, sinϕ =				3	= 0,866 .
	2		3			2

На плиту действует произвольная пространственная система сил, для равновесия которой необходимо и достаточно шесть условий (уравнений) равновесия. Число неизвестных реакций шесть: X A , YA ,

ZA , YВ, ZВ и RC . Следовательно, задача является статически определимой.

Записываем условия равновесия и составляем уравнения равновесия:

Для определения моментов силы RС и F воспользуемся теоремой Вариньона о моменте равнодействующей

mx (RC ) = mx (RCх ) + mx (RCу ) + mx (RCz ) = 0 + 0 + RC sinα b,

(2)

my (RC ) = my (RCx ) + my (RCy ) + my (RCz ) = 0 + 0 − RC sinα a,

mz (

RC ) = 0.

mx (

) = mx (

F

Fy ) + mx (Fz ) = 0 + F cos β b,

my (

) = my (

a

= −F cos β

a

,

(2’)

F

Fy ) + my (

Fz ) = 0 − F cos β

3

3

a

m

(

) = m

(

) + m

(

) = −F sin β DE + 0 = −F sin β

.

F

F

F

z

z

y

z

z

3

n

∑Fkx

= 0,

X A − RС cosα cosϕ = 0,

(3)

k =1

n

YA − RC cosα sinϕ − F sin β +YB = 0,

∑ Fky = 0,

(4)

k =1

n

Z A + ZB −G + RC sinα + F cos β = 0,

∑Fkz

= 0,

(5)

k =1

n

∑mx (

Fk ) = 0,

RС sinα b + F cos β b −G 0,5b − M = 0,

(6)

k =1

a

n

G 0,5a − ZB

a − RC sinα a − F cos β

= 0,

∑ m

y

(

F

) =

0,

(7)

k =1

k

a

3

n

YB a − F sin β

= 0.

∑m

(

F

) = 0,

(8)

k =1

z

k

3

Решаем систему уравнений (3) – (8).

Из уравнения (8) определяем YB:

YB =

F sin β a

=

5sin 60°

=1,44 кН.

3a

3

Из уравнения (6) определяем RC:

R

=

0,5G b − F bcos β + M

= 11,7 кН.

C

bsinα

Из уравнения (7), сократив а, определяем ZB:

ZB = 0,5G − RC sinα − F 13 cos β = −4,11 кН.

Из уравнения (5) определяем ZА:

Z A = G − ZB − RC sinα − F cos β = 3,34 кН.

Из уравнения (4) определяем YА:

YA = RC cosα sinϕ + F sin β −YB =10,05 кН.

Из уравнения (3) определяем ХА:

X A = RC cosα cos β = 4,14 кН.

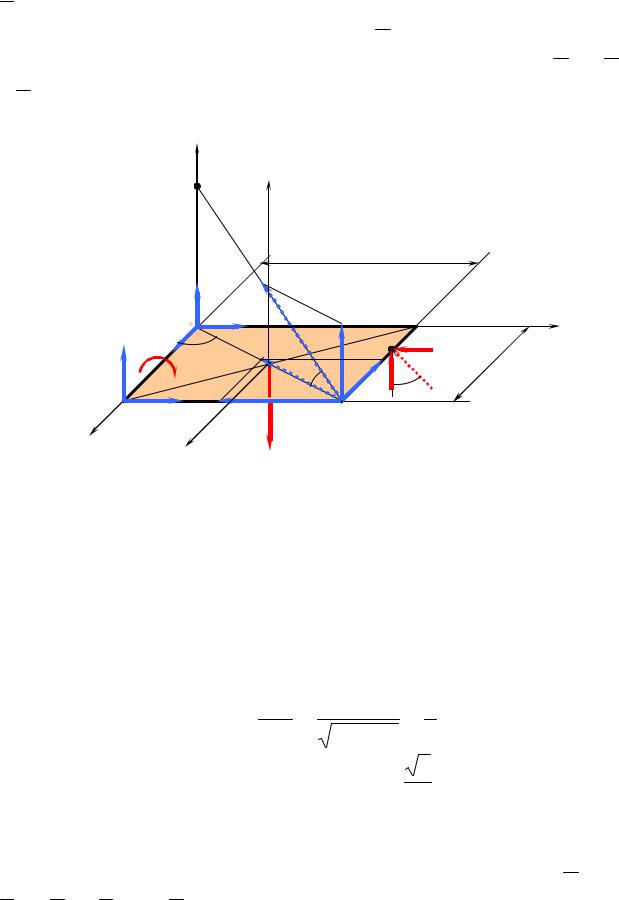
Выбираем новые оси координат x1 и z1 и, учитывая (1) и (2), составляем проверочные уравнения моментов относительно этих осей:

			n
			∑mx1	(		Fk ) = 0,
		k =1
− ZB 0,5b − Z A 0,5b − M + RC sinα 0,5b + F cos β 0,5b = 0.										(9)
			n
			∑mz1	(	Fk ) = 0,
		k =1							sinϕ 1 a +
Y	1 a + X	1 b −Y	1 a − R cosα
	B 2	A 2	A 2			C			2	(10)
		cosϕ 1 b + F sin β( 2							− 1)a = 0.
+ R cosα
	C	2		3					2

Подставляя значения в уравнения (9) и (10) и решаем их:

4,11 3 − 3,34 3 − 20 +11,7 sin 45° 3 + 5 cos 60° 3 = 0, 25,78 – 25,78 = 0, 0 ≡0.

1,44 + 4,14 3 −10,05 −11,7 cos 45°sin 60°+11,7 cos 45°cos 60° 3 + + 5sin 60°13 = 0,

17,16 −17,16 = 0, 0 ≡0.

Задача решена правильно.