МУ ТМ_2015 / Кинематика Т.1 (Живаго, Желтухин, Ермаченко)

Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования

«Сибирский государственный индустриальный университет»

Кафедра технической механики и графики

КИНЕМАТИКА ТЕМА 1. КИНЕМАТИКА ТОЧКИ

Методические указантя по выполнению расчетно-графических работ

по дисциплине «Теоретическая механика» для студентов очной формы обучения

Новокузнецк

2014

УДК 378. 147 К41

Рецензент доктор технических наук, профессор, зав. кафедрой

автомобильного транспорта и технологических машин СибГИУ А.Г. Никитин

К41 Кинематика. Тема 1. Кинематика точки : метод. указ. /Сиб. гос. индустр. ун-т. ; сост. : Э.Я. Живаго, Д.В. Желтухин, М.В. Ермаченко. – Новокузнецк : Изд. центр СибГИУ, 2014. – 44 с.

Включают краткую теоретическую часть, примеры решения задач, рекомендации для выполнения самостоятельной работы, 25 вариантов индивидуальных комплексных заданий по 6 задач в каждом варианте.

Рекомендуются для студентов очной формы обучения.

2

КИНЕМАТИКА

Кинематикой называется раздел механики, в котором изучается движение материальных объектов с геометрической точки зрения, т.е. без учета их массы и действующих на них сил.

При изучении раздела выделяются кинематика точки и кинематика твердого тела.

Тема 1. КИНЕМАТИКА ТОЧКИ

Изучение движения точки заключается в определении характеристик её движения: положения точки в заданный момент времени в выбранной системе координат, траектории движения, скорости и ускорения.

Траекторией точки называется геометрическое место последовательных (с течением времени) положений её в пространстве, определяемое в той или иной системе отсчёта.

Кинематически задать движение (закон движения) точки – значит задать ее положение относительно выбранной системы координат в любой момент времени. Математические выражения, определяющие положение точки в любой момент времени в выбранной системе координат, называются уравнениями движения (законами движения) точки. Зная закон движения, можно определить основные кинематические характеристики движения.

Существует три основных способа задания движения точки: векторный, координатный и естественный.

При векторном способе задания движения положение точки задается её радиус-вектором r , как функцией времени, проведенным из какого-то неподвижного центра. Уравнение движения записывается в виде

r r(t).

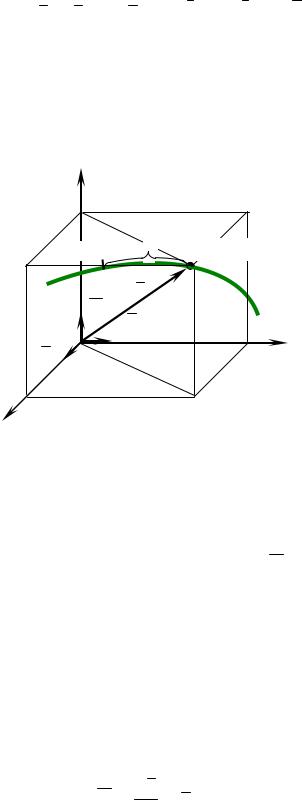
При координатном способе задания движения положение точки определяется её координатами в прямоугольной декартовой системе (рисунок 1). Координаты являются функциями времени, и уравнения движения точки записываются в виде

x x(t), у у(t), z z(t).

3

Очевидна связь между векторным и координатным способами задания движения

r r (t), r x i у j z k .

При естественном способе задания движения положение точки на заданной траектории определяется её дуговой координатой S S t (рисунок 1).

Задается начало отсчета (точка О1), положительное и отрицательное направления отсчёта дуговой координаты.

	z
(−)O1 (+)				S	М(х,у,z)
		k	r		zM
	O		j			у
i
			уМ			xМ
х

Рисунок 1 – Естественный способ задания движения точки

Основными кинематическими характеристиками движения точки являются её скорость и ускорение. Это векторные величины имеющие размерности, соответственно, м/с и м/с2.

Скоростью точки называется вектор V , определяющий в каждый момент времени быстроту изменения положения и направление движения точки в выбранной системе отсчёта.

Вектор скорости точки в данный момент времени направлен по касательной к траектории (рисунок 2). При прямолинейном движении вектор скорости совпадает с траекторией и направлен в сторону движения.

При векторном способе задания движения скорость точки определяется как первая производная по времени от радиус-вектора

V ddrt r .

При координатном способе задания движения скорость определяется через проекции вектора скорости на выбранные координатные оси

4

VVx i V у j Vz k , Vx dxdt x, V у ddуt у, Vz dzdt z .

Проекция вектора скорости на координатную ось равна

алгебраическому значению первой производной по времени от соответствующей координаты точки.

Численное значение скорости определяется геометрическим сложением

V = V 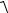Vx2 V у2 Vz2 .

При естественном способе задания движения числовое (или алгебраическое) значение скорости точки определяется как первая производная по времени от дуговой координаты

V dSdt S .

a

V

n

a

aп

п

Рисунок 2 – Скорость и ускорение точки

Ускорение точки a характеризует быстроту изменения вектора скорости по величине и направлению.

Вектор ускорения точки находится в соприкасающейся плоскости траектории точки, т.е. в плоскости М n (рисунок 2), и направлен в сторону вогнутости траектории. При прямолинейном движении вектор ускорения совпадает с траекторией движения точки.

При векторном способе задания движения ускорение точки равно или первой производной по времени от вектора скорости точки, или второй производной по времени от радиус-вектора точки

a ddVt V r .

5

При координатном способе задания движения ускорение точки определяется через проекции вектора ускорения на выбранные координатные оси

a ах· i + ау· j + аz· k ,

ах = Vx x , ау = V у у, аz =Vz z , а = a 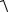a x2 a 2у a z2 .

При естественном способе задания движения ускорение точки проецируется на оси естественного трехгранника – на касательную ось М и на главную нормаль Мn (рисунок 2)

a a an n или a a an ,

где и n − единичные векторы касательной и главной нормальной осей естественного трёхгранника.

Проекция ускорения точки на касательную ось a (касательное

ускорение) равна первой производной по времени от числового значения скорости точки или второй производной по времени от дуговой координаты точки и характеризует изменение скорости по

величине a V S .

Проекция ускорения на главную нормальную ось an (нормальное ускорение) характеризует изменение вектора скорости

по направлению и определяется выражением an V 2 , где - радиус

кривизны траектории в данной точке.

Так как a	a	n	, то а =	a 2	a 2 .
					n
Если V S и a =V S имеют одинаковые знаки, то векторы

V и a направлены в одну сторону, и движение точки будет ускоренным. В противном случае – движение точки замедленное.

Примеры выполнения и оформления задач

Задача 1. По заданным уравнениям движения точки М установить вид ее траектории и для момента времени t = 1 с, определить положение точки на траектории, ее скорость, полное, касательное и нормальное ускорения, а так же радиус кривизны траектории.

6

Исходные данные: x 2cos 4t см, y 1 4sin 4t см, t = 1c.

Найти: у = (x); x; у; Vx; Vу; V; ax; aу; a; a ; an; .

РЕШЕНИЕ:

1) Определяем траекторию точки М и её положение в данный момент времени.

Выражаем синус и косинус функции 4t , возводим их в квадрат и складываем. Получаем функцию:

	x 2		( y 1)2	1.
	4		16

Траекторией точки является эллипс в пределах - 2 х 2 ,

-3 у 5 (рисунок 3). При t = 1 c

х= 2 cos 4 1,4 см, у = 1 4sin 4 = 3,8 см.

2)Определяем скорость точки:

Вектор скорости V Vx i V y j . Проекции вектора скорости:

Vx x 2 sin 4t , V y = y cos 4t ,

при t = 1 c

Vx 12 0,7 1,1 см/с; Vy 0,7 2,2 см/с.

Модуль вектора скорости

V 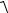Vx2 Vy2 ( 1,1)2 2,22 2,5см/с.

7

				n
			- 3
			- 2			an
			- 1 a			3 a x 4 5	6		у
- 3	- 2	- 1	0	1	2	Vx		V
				a y
			1			M		Vу
			2
						aτ
			3
			х
	Рисунок 3 – Скорость и ускорения точки

Вектор скорости строим по его составляющим, параллельным координатным осям V Vx i Vy j (рисунок 3).

3) Определяем ускорение точки.

Вектор ускорения a a x i a y j . Проекции вектора ускорения:

		2		t			2		t
a x Vx			cos		, a y V y			sin		.
	x	8		4		y	4		4
При t = 1 c, ax 0,86 см/с2, a y 1,72 см/с2.

Модуль ускорения

a 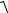ax2 a2y 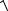( 0,86)2 ( 1,72)2 1,93 см/с2.

Строим вектор ускорения по его составляющим, параллельным координатным осям (рисунок 1.3).

4) Касательное и нормальное ускорения.

Величину касательного ускорения находим по формуле

a	Vх aх Vу a у			( 1,1) ( 0,86) 2,2 ( 1,72)	1,1	2
						см/с .
		V		2,5

Знак ''–'' показывает, что касательное ускорение не совпадает по направлению с вектором скорости (замедленное движение).

Находим величину нормального ускорения

8

a	n		a2 a2		1,932 ( 1,1)2	1,58 см/с2.

5)Радиус кривизны траектории

V 2 2,52 4,2 см. an 1,58

Результаты вычислений сведены в таблицу 1.

	Таблица 1.
Координаты,			Скорость,				Ускорение,				,
	см			см/с			ax	см/с2			см
х		у	Vx	Vy	V	ax		aп	a	a
1,4		3,8	1,1	2,2	2,5	0,86	1,72	1,58	1,1	1,93	4,2

Задача 2. По заданным уравнениям движения точки М установить вид ее траектории и для момента времени t = 1с найти положение точки на траектории, ее скорость, полное, касательное и нормальное ускорения, а так же радиус кривизны траектории.

	Исходные данные: x t 3 см,	y sin	t 3	см, t = 1 c.
			3

Найти: у = (x); x; у; Vx; Vу; V; ax; aу; a; a ; an; .

РЕШЕНИЕ

1) Определяем траекторию точки и её положение в данный момент времени методом избавления от параметра времени

y sin 3x .

Траекторией точки является часть синусоиды в пределах 0 х , - 1 у 1 (рисунок 4).

При t = 1 c, y = sin

t 3

0,866 см,

x = t 3

= 1 см.

3

2) Определяем скорость точки М:

Вектор скорости

Vx

V y

.

V

i

j

Проекции вектора скорости:

t 3

Vx =

2

, V y

t

2

cos

,

x 3t

y

3

9

при t = 1 c,		Vx	3 см/с,	Vy	0,5 1,57 см/с.
у			V
	Vу	aτ
1			Vx
	M			ах
0							х
				3	4	5	6
- 1	ау		an	a
			п
		Рисунок 4 – Решение задачи 2

Модуль вектора скорости

V Vx2	Vy2	32 1,572 3,39 см/с.
Вектор скорости строим по его составляющим, параллельным
координатным осям V 1	Vx1 i V y1 j (рисунок 4).

3) Определяем ускорение точки.

Вектор ускорения a a x i a y j . Проекции вектора ускорения:

t 3

2

4

t 3

a x Vx

6t , a y V y

t

sin

.

x

y 2 t cos

3

3

При t = 1 c, ax

6 см/с2,

a y

6,73 см/с2.

Модуль ускорения

a

ax2 a2y

62 ( 6,73)2

9,01 см/с2.

Строим вектор ускорения по его составляющим, параллельным

координатным осям (рисунок 4).

4) Касательное и нормальное ускорения.

Величину касательного ускорения находим по формуле

a

Vх aх

Vу a у

3 6 1,57 ( 6,73)

2,2 см/с2

V

3,39

10