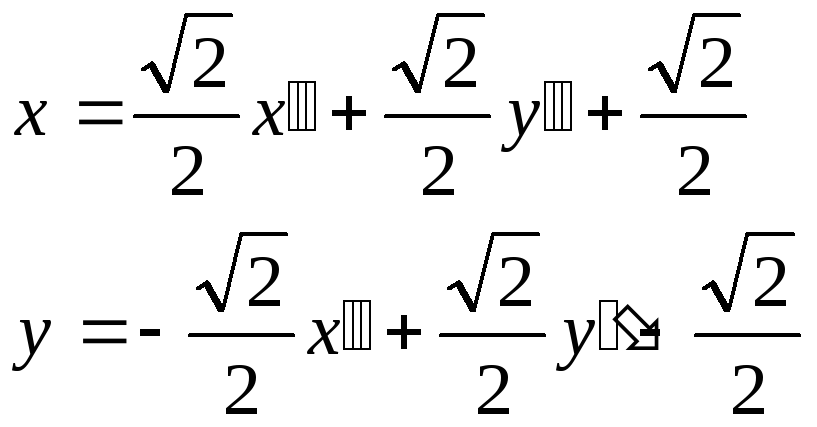Лекция №14
Классификация линий второго порядка. Приведение линии второго порядка к каноническому уравнению и построение ее точек в системе координат
Классификация линий второго порядка.
Идея классификации линий второго порядка заключается в том, чтобы путём надлежащего выбора системы координат упростить уравнение линии, а затем определить по этому уравнению, к какому классу эта линия принадлежит.
При классификации возможны следующие преобразования системы координат: 1) поворот вокруг начала координат;
2) параллельный перенос начала координат; 3) параллельный перенос осей координат и т.д.
Пусть линия второго
порядка
![]() в прямоугольной системе координат
задана уравнением:
в прямоугольной системе координат
задана уравнением:
![]() (1)
(1)
Рассмотрим поворот
системы координат вокруг точки
![]() так, чтобы вектор
так, чтобы вектор
![]() в новой системе
в новой системе
![]() имел главное, но не асимптотическое
направление, тогда
имел главное, но не асимптотическое
направление, тогда
![]() будет иметь также главное направление.
будет иметь также главное направление.
Запишем уравнение
линии второго порядка
![]() в новой системе координат:
в новой системе координат:
![]() .
.
Так как
![]() имеет главное направление, то его
координаты удовлетворяют уравнению:
имеет главное направление, то его
координаты удовлетворяют уравнению:
![]()
![]()
![]()
![]()
![]() .
.
Вектор
![]() не имеет асимптотического направления,
значит
не имеет асимптотического направления,
значит
![]() .
.
Таким образом,
уравнение (1) линии второго порядка в
новой системе координат примет вид:
![]() (2)
(2)
Дальнейшее упрощение
линии второго порядка достигается путём
надлежащего выбора точки
![]() и переноса начала координат в в эту
точку.
и переноса начала координат в в эту
точку.
Классификация центральных линий второго порядка.
Так как в центральной
линии центр является центром симметрии,
то точку
![]() необходимо выбрать таким образом, чтобы
она являлась центром симметрии данной
линии в новой системе координат, т.е.
коэффициенты при переменных
необходимо выбрать таким образом, чтобы
она являлась центром симметрии данной
линии в новой системе координат, т.е.
коэффициенты при переменных
![]() и
и
![]() .
.
![]() .
Уравнение (2) примет вид:
.
Уравнение (2) примет вид:
![]() (3).
(3).
Разделив обе
части равенства (3) на
![]() имеем:
имеем:
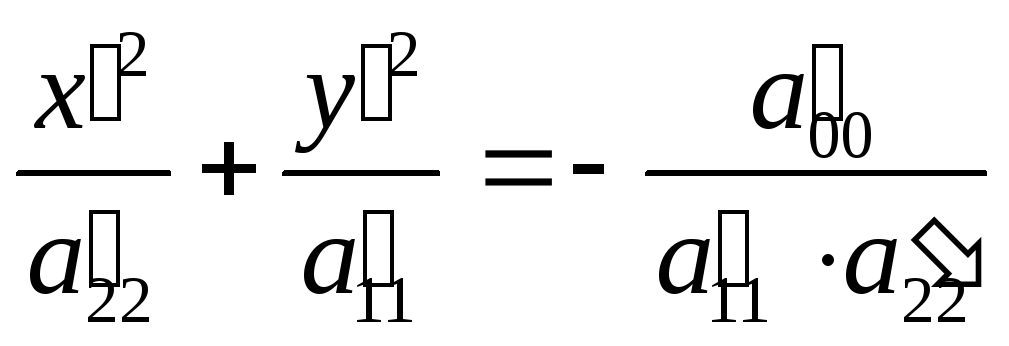 .
.
Возможны два случая:
1)
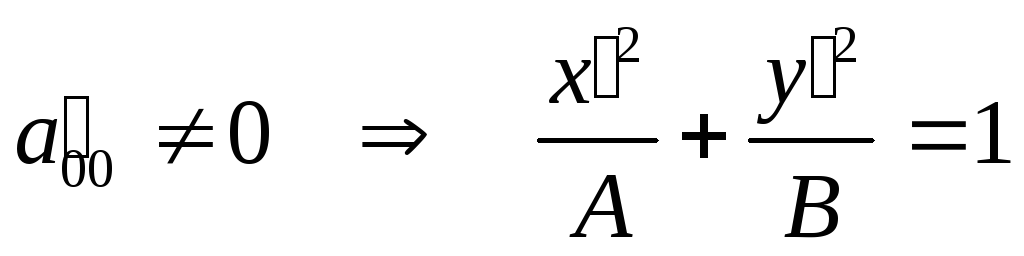 ,
где
,
где
![]() а)
а)
![]() эллипс
эллипс
б)
![]() гипербола
гипербола
в)
![]() - мнимый эллипс
- мнимый эллипс
г)
![]() - мнимая гипербола
- мнимая гипербола
2)
 ,
где
,
где
![]()
а)
![]() пара мнимых пересекающихся в действительной
точке (0,0) прямых
пара мнимых пересекающихся в действительной
точке (0,0) прямых
![]() ;
;
б)
 пара пересекающихся прямых.
пара пересекающихся прямых.
Классификация нецентральных линий второго порядка.
Перенесём начало
координат системы
![]() в один из центров линии второго порядка.
В данном случае вектор
в один из центров линии второго порядка.
В данном случае вектор
![]() имеет асимптотическое направление.
Тогда уравнение (3) линии второго порядка
с учётом условий асимптотического
направления запишется следующим образом:
имеет асимптотическое направление.
Тогда уравнение (3) линии второго порядка
с учётом условий асимптотического
направления запишется следующим образом:
![]() ,где
,где
![]() ;
;
а) Пусть
![]() и
и
![]()
![]() - две параллельные прямые;
- две параллельные прямые;
б) Пусть
![]() и
и
![]()
![]() - пара мнимых параллельных прямых;
- пара мнимых параллельных прямых;
в)
![]() - линия распадается на пару совпавших
прямых.
- линия распадается на пару совпавших
прямых.
Классификация нецентральных линий второго порядка, не имеющих центра.
В этом случае
перенос начала координат совершается
в точке![]() ,
лежащую на главном диаметре линии
,
лежащую на главном диаметре линии
![]() .
Вектор
.
Вектор
![]() имеет асимптотическое направление.
Коэффициенты
имеет асимптотическое направление.
Коэффициенты
![]() ,
тогда уравнение принимает вид:
,
тогда уравнение принимает вид:
![]()
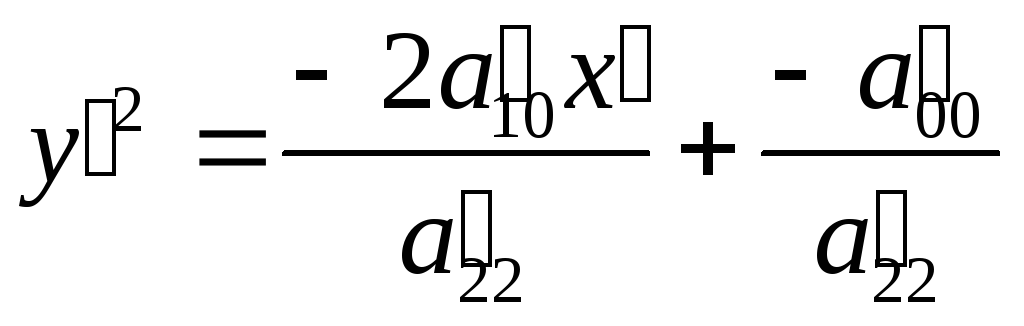
Так как
![]() , то
, то
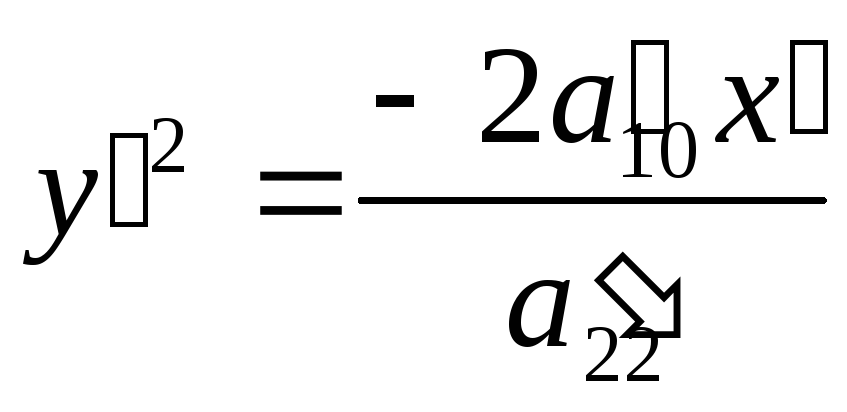 или
или
![]() ,
где
,
где
![]() -
уравнение задаёт параболу.
-
уравнение задаёт параболу.
Приведение уравнения линии второго порядка к каноническому виду и построение её точек.
Общая схема:
1. Написать
соответствующее характеристическое
уравнение
![]() .
Найти его корни;
.
Найти его корни;
-
Найти координаты векторов главных направлений
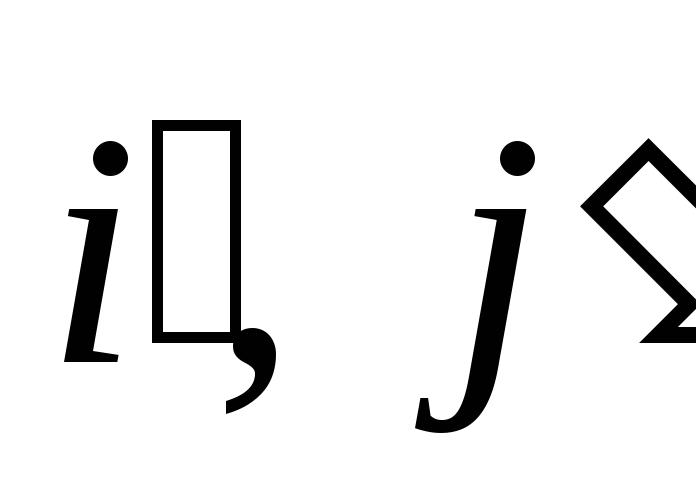 и принять их за направление новых
координатных осей :
и принять их за направление новых
координатных осей :
 ,
где
,
где
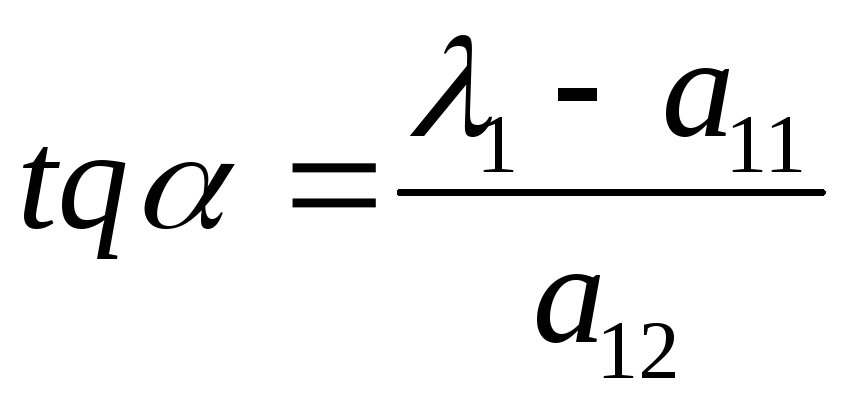

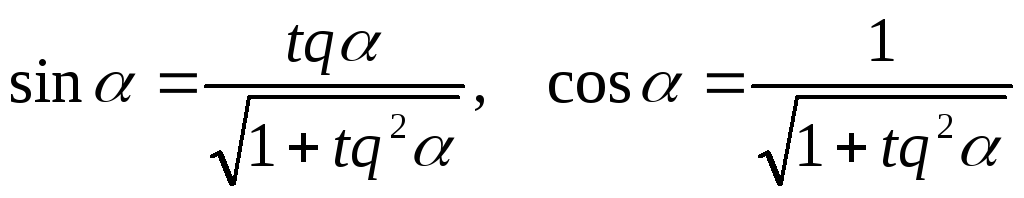 .
.
3. Записать формулы
преобразования координат:
![]() .
.
4. Вычислить коэффициенты:
![]()
![]()
![]()
![]()
![]()
Из этих формул
следует, что
![]() .
Но по формуле Виета (когда находим
.
Но по формуле Виета (когда находим
![]() )
и, учитывая коэффициенты нового уравнения,
получаем:
)
и, учитывая коэффициенты нового уравнения,
получаем:
![]() .
.
5. Записать уравнение
линии в системе
![]() :
:
![]()
6. Перенести начало
координат, записав формулы преобразования
координат
![]() .
.
7. Записать
получившееся уравнение линии второго
порядка в системе
![]() и привести его к каноническому виду
и привести его к каноническому виду
8.Построить систему
координат
![]() по координатам точки
по координатам точки
![]() и
и
![]() .
Затем построить точки канонического
уравнения линии второго порядка;
.
Затем построить точки канонического
уравнения линии второго порядка;
9. Записать формулы
преобразования координат системы
![]() в систему
в систему
![]()
Пример.
Привести уравнение линии второго порядка
к каноническому виду:
![]() .
.
Решение:
1. Запишем
характеристическое уравнение линии
второго порядка:
![]()
![]()
![]()
![]()
2. Найдем координаты
векторов главных направлений
![]() :
:
![]()
![]()
![]()
![]()
![]()
Значит,
![]()
3. Формулы
преобразования координат системы
![]() в
систему
в
систему
![]()
![]()
4. Найдём числовые коэффициенты:
![]()
![]()
![]() примут вид:
примут вид:
![]()
5. Уравнение линии
второго порядка в системе
![]() примет
вид:
примет
вид:
![]() (*)
(*)
6. Определим
координаты нового центра
![]() .
Так как
.
Так как
![]() ,
то линия центральная, а значит,
имеет место быть система уравнений:
,
то линия центральная, а значит,
имеет место быть система уравнений:
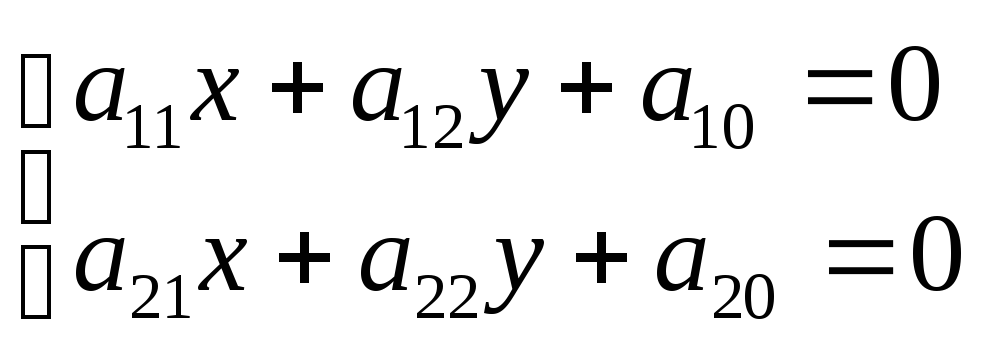
![]()

Формулы преобразования
координат, переводящие
![]() :
:
![]()
7. Запишем уравнение
линии в системе
![]() ,
подставив выражения для значений
,
подставив выражения для значений
![]() в (*):
в (*):
![]()
![]()
![]()
![]()
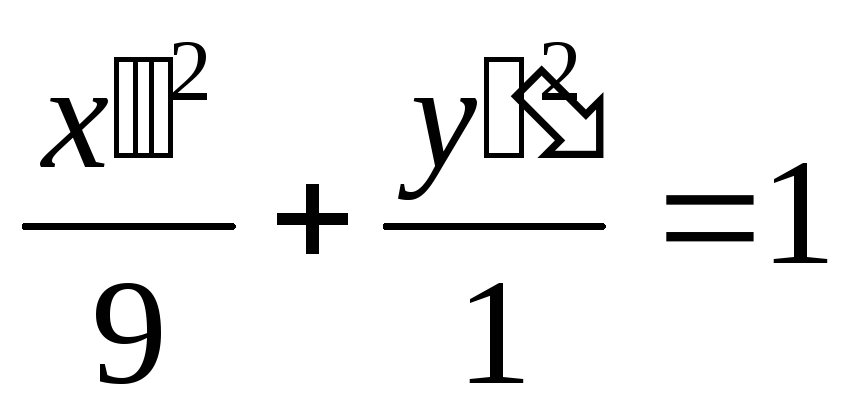 - эллипс с полуосями
- эллипс с полуосями
![]() .
.
8. Построение.

9. Формулы перехода
![]() :
:
![]()
![]()
![]()