ГОСЫ / вопрос 15 / Лекция 4

Лекция №4

Вектор функции 2-х скалярных аргументов. Предел. Дифференцирование. Понятие поверхности. Гладкие поверхности и их параметризация с помощью вектор функции.

Пусть дано векторное пространство V₃ и двумерная область ²₊ . Поставим по некоторому закону двум числам некоторый вектор ₃.

Определение 4.1. Соответствие f области G векторному пространству V₃ называется вектор функция 2-х скалярных аргументов .

Определение 4.2. Вектор функция 2-х скалярных аргументов называется бесконечно малой в точке (u₀,v₀) из области G, если числовая функция

при _{0, 0} , либо

Определение 4.3. Пределом вектор функции 2-х скалярных аргументов

при ₀, ₀ называется такой постоянный вектор , что есть бесконечно малый вектор вблизи точки (u₀,v₀).

Определение 4.4. Векторная функция двух скалярных аргументов, называется непрерывной в точке (u₀,v₀), если

Так как , а вектор (₁, ₂, ₃), то

, ,

Рассмотрим ₀-const, тогда имеем вектор функция одного скалярного аргумента и _u

Аналогично определяется частная производная по параметру v.

,

Определение 4.5 Вектор называется дифференциалом векторной функции 2-х скалярных аргументов в точке (u,v) или

Определение 4.6. Вектор функция двух аргументов называется дифференцируемой в точке (u,v), если дифференцируемы соответствующие ей скалярные функции в этой же точке.

Определение 4.7. Функция 2-х скалярных аргументов называется дифференцируемой в области G, если она дифференцируема в каждой точке области.

Понятие поверхности.

Определение 4.8. Простейшей поверхностью в пространстве будем называть следующие поверхности: плоскость, замкнутая полуплоскость, квадрат.

Определение 4.9. Элементарной поверхностью называется фигура, которую можно покрыть счетным или конечным множеством элементарных поверхностей.

Определение 4.10. Точка М принадлежащая поверхности называется обыкновенной, если у неё существует такая окрестность, что пересечение поверхностей с этой окрестностью является элементарной линией:

а) пересечение гомеоморфно плоскости – точка внутренняя.

б) пересечение гомеоморфно замкнутой плоскости - точка М- граничная.

Определение 4.11. Точка поверхности называется особой (топологически особой), если она не является обыкновенной.

Определение 4.12. Поверхность, все точки которой являются обыкновенными, называется простой.

Определение 4.13. Совокупность всех граничных точке поверхности называется её границей или краем.

Любую поверхность можно задать двумя способами:

• Векторным уравнением: :

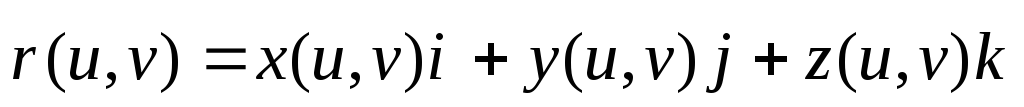• Параметрически:

Пусть точка M(x,y,z)- ее радиус вектор (точки, описывающий поверхность).

Определение 4.14. Поверхность F₀ называется гладкой класса С^к (регулярный класс С^к), где k, если соответствующая ей вектор функция 2-х скалярных аргументов имеет в области G непрерывные частные производные до k- порядка, включительно, причем в каждой точке (u,v)

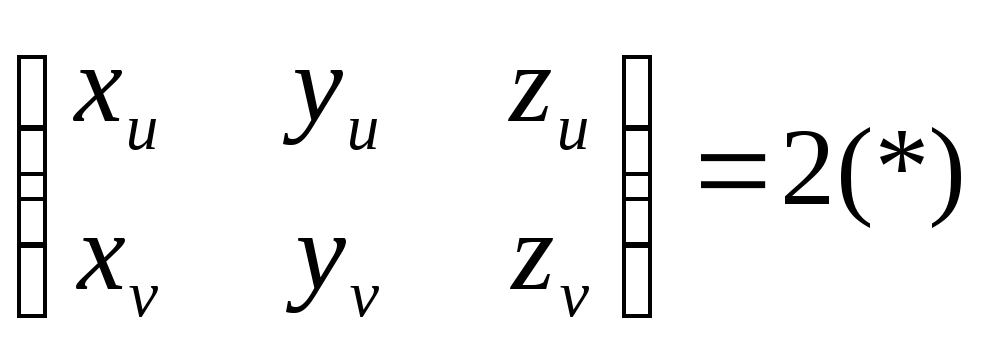
Условие (*) означает, что векторы частных производных линейно независимы в области G и значит, в точке принадлежащей G.

Определение 4.15. Простая поверхность называется гладкой класса С^к , если у каждой её внутренней точки М, существует окрестность такая что пересечение поверхности с этой окрестности есть гладкая поверхность класса С^к .

Пусть вектор-функция r(u,v):v=v₀ =constлиния, называемая U- линией U=U₀=const , r=r(u₀,v)=v - линия.

Совокупность U и V- линий определяет координатную сеть поверхности, причем каждая U и V линии пересекаются в одной точке. Если известны значения параметров u,v , то по параметрическим уравнениям поверхности можно определить координатнаты точки М этой поверхности.

Определение 4.16. Параметры U и V называются криволинейными координатами точки поверхности.

Параметризация.

Для замены параметров необходимо:

1) Задать некоторый гомеоморфизм:

2) и должны быть непрерывными функциями U и V определенными в G,

т.е. (1)

3) Так как заданный гомеоморфизм является биекцией, то уравнения (1) однозначно разрешимы относительно U и V, т.е.

4) Записать параметрическое уравнение поверхности, поменяв параметры U и V от параметров и .