
Лекция №2
Векторы в пространстве. Векторное произведение векторов.
Геометрический смысл векторного произведения. Площадь треугольника.
Задание 1. Провести аналогию тем «Векторы на плоскости» и «Векторы в пространстве», заполнив таблицу.
|
Основные вопросы |
Векторы на плоскости |
Векторы в пространстве |
|
Определение: |
|
|
|
Виды векторов |
|
|
|
Координаты вектора |
|
|
|
Разложение вектора по базисным векторам |
|
|
|
Длина вектора |
|
|
|
Действия над векторами в геометрической форме |
|
|
|
Свойства действий |
|
|
|
Действия над векторами в координатах |
|
|
|
Угол между векторами |
|
|
Теорема 2.1. Если
векторы
![]() ,
,
![]() и
и
![]() не компланарны, то для любого вектора
не компланарны, то для любого вектора
![]() существуют единственные числа
существуют единственные числа
![]() и
и
![]() такие, что
такие, что
![]()
Доказательство:
-
Докажем, что
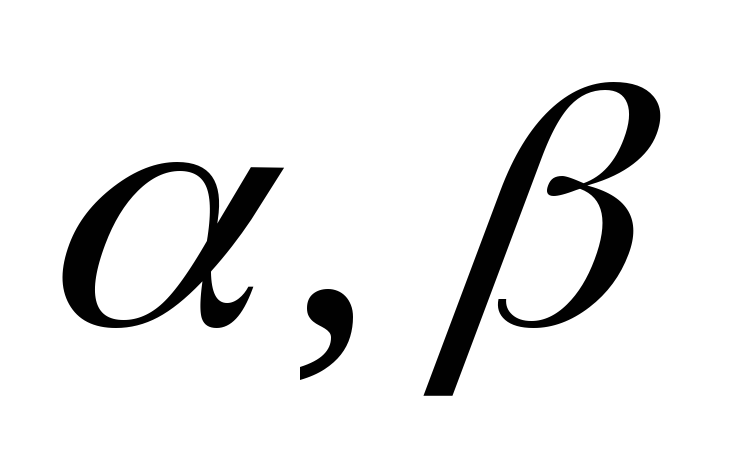 и
и
 существуют.
существуют.
-
Отложим от некоторой точки О плоскости векторы
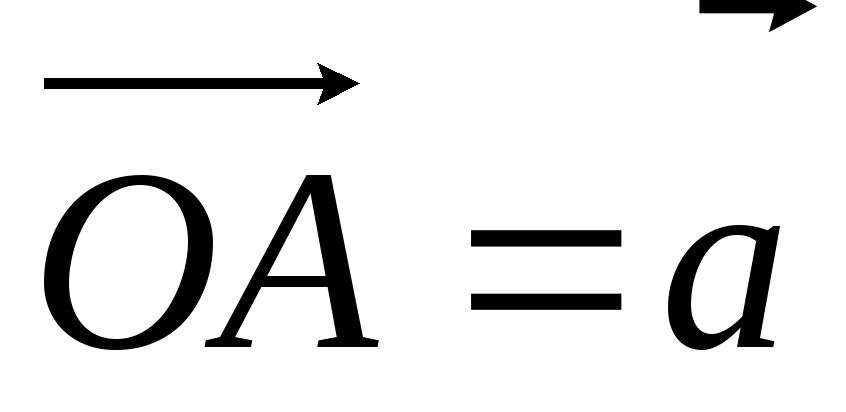 ,
,
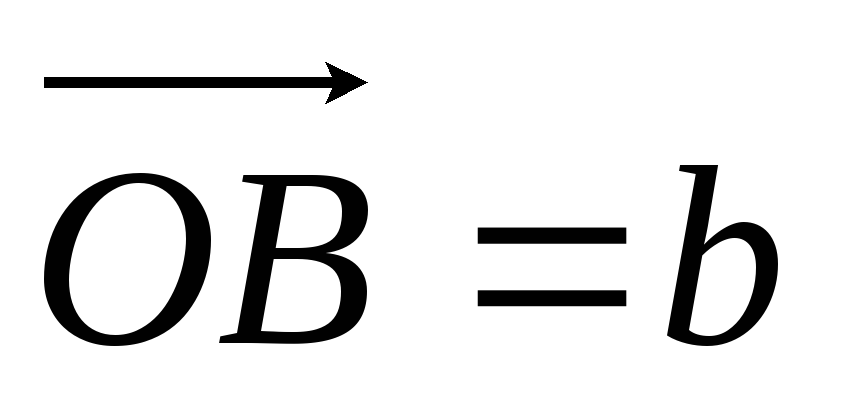 ,
,
 ,
,
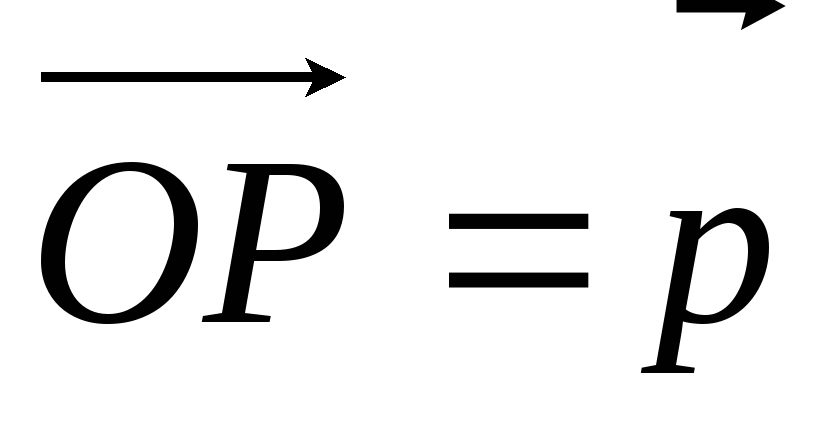 .
Так как
.
Так как
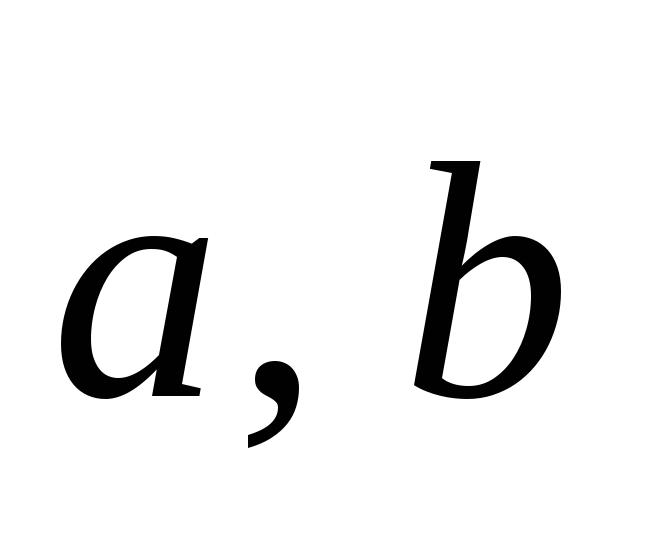 и
и
 не компланарны, то точки
не компланарны, то точки
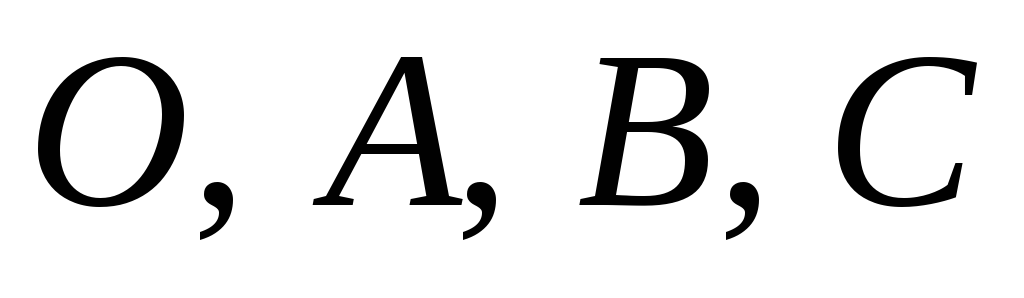 не лежат в одной плоскости.
не лежат в одной плоскости. -
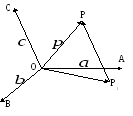 Если
точка
Если
точка
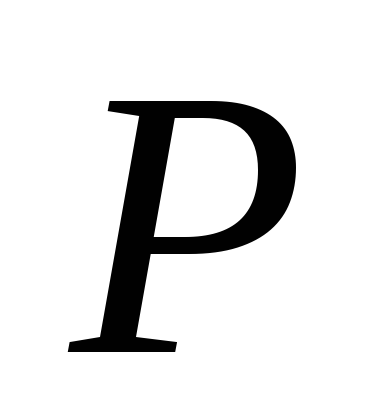 лежит на прямой
лежит на прямой
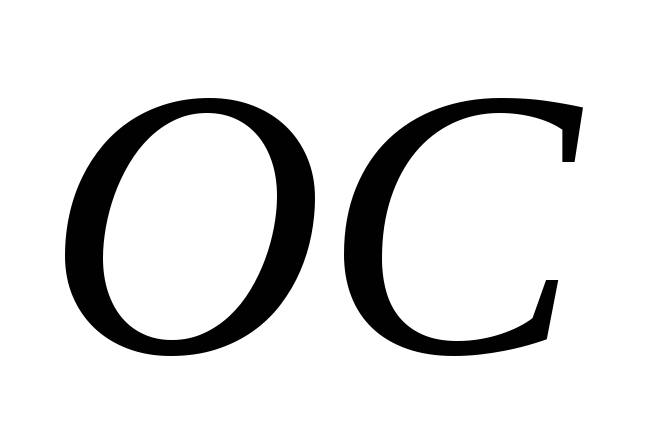 ,
то векторы
,
то векторы
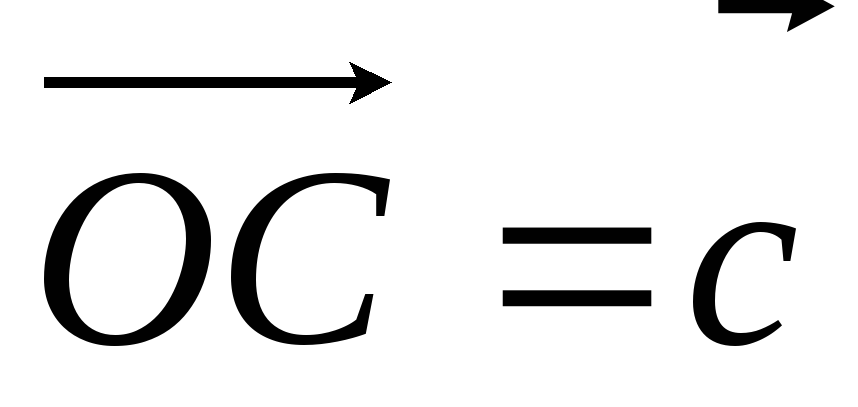 и
и
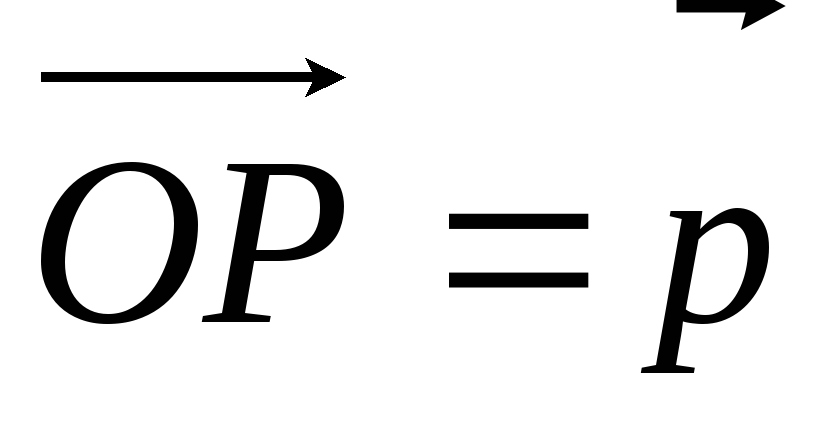 коллинеарны, поэтому по теореме о
коллинеарных векторах
коллинеарны, поэтому по теореме о
коллинеарных векторах
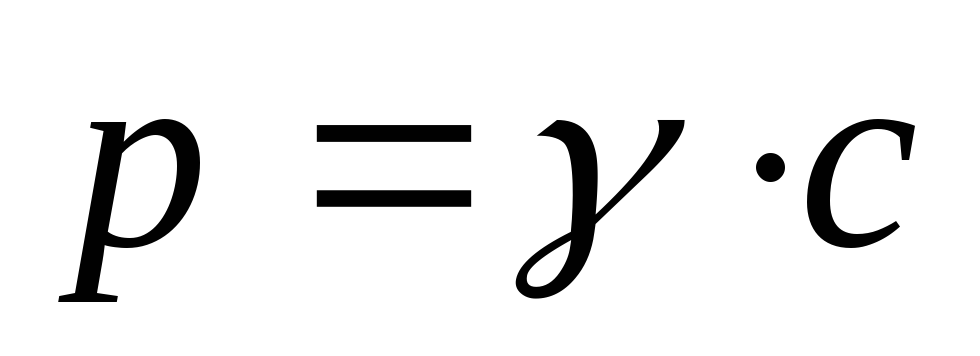 или
или
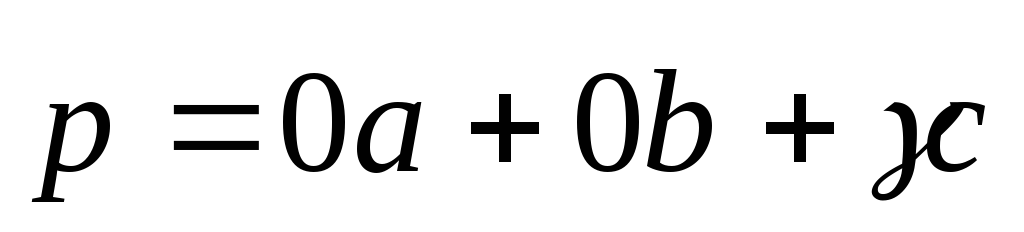 .
Аналогично в случаях расположения
точки
.
Аналогично в случаях расположения
точки
 на
прямых
на
прямых
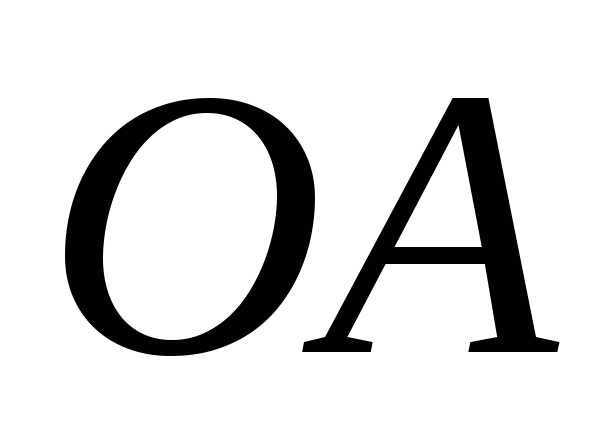 и
и
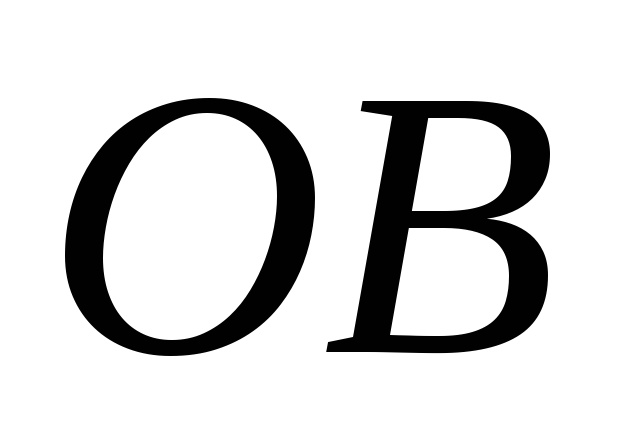 .
. -
Рассмотрим случай, когда точка
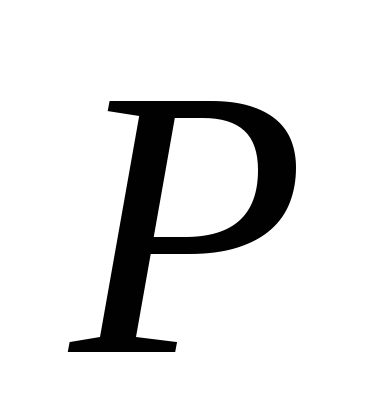 не принадлежит ни одной из указанных
прямых.
не принадлежит ни одной из указанных
прямых.
-
Проведем через точку
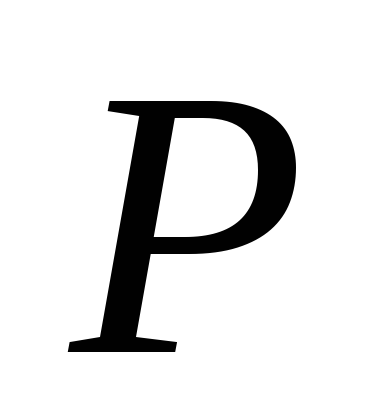 прямую
прямую
 ,
параллельную прямой
,
параллельную прямой
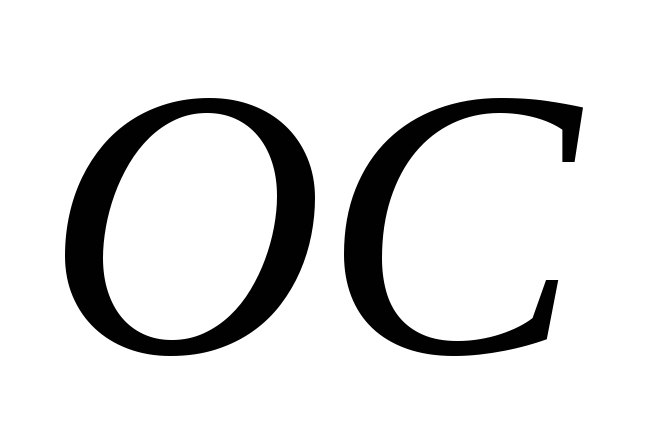 ,
где
,
где
 - точка пересечения этой прямой с
плоскостью
- точка пересечения этой прямой с
плоскостью
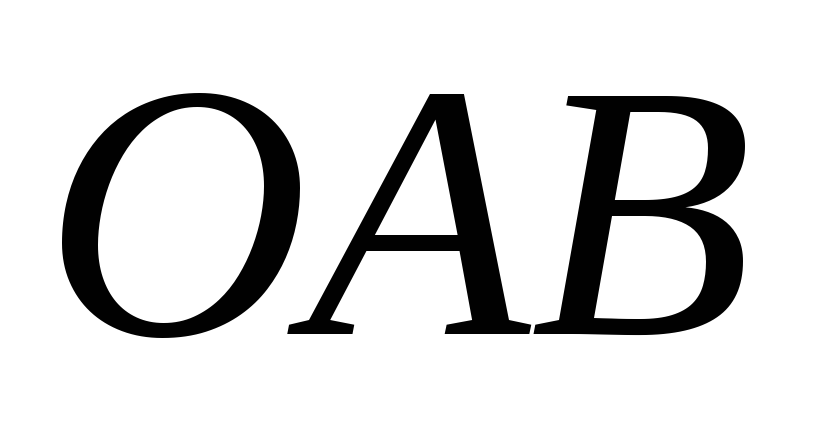 ;
; -
Так как векторы
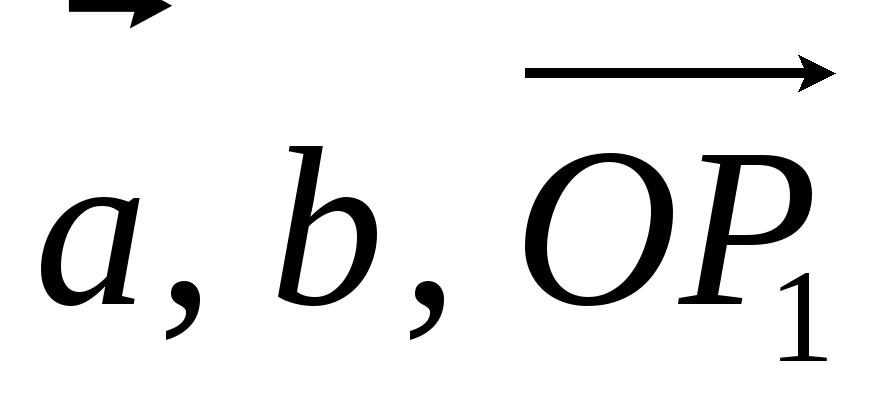 компланарны, то по теореме 2. 2 имеем,
что
компланарны, то по теореме 2. 2 имеем,
что
 ;
; -
Так как векторы
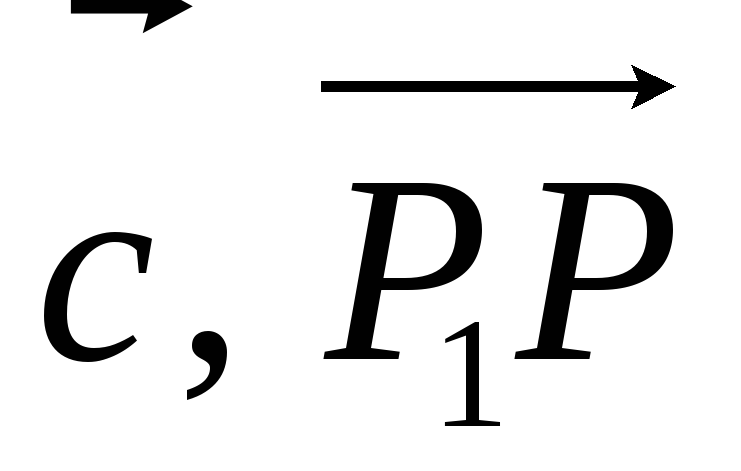 коллинеарны по построению, то по теореме
2.1 имеем, что
коллинеарны по построению, то по теореме
2.1 имеем, что
 ;
; -
По правилу треугольника
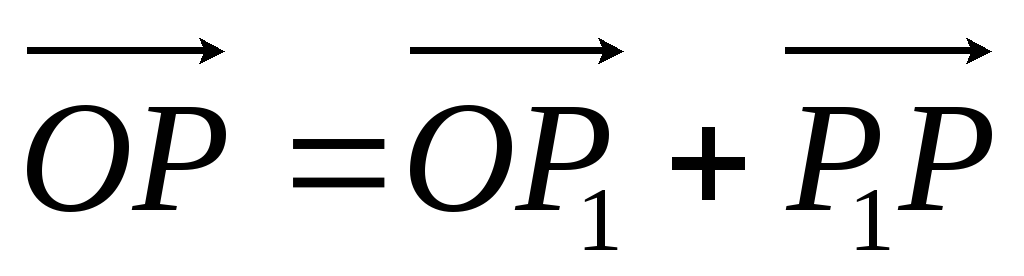 ,
поэтому
,
поэтому
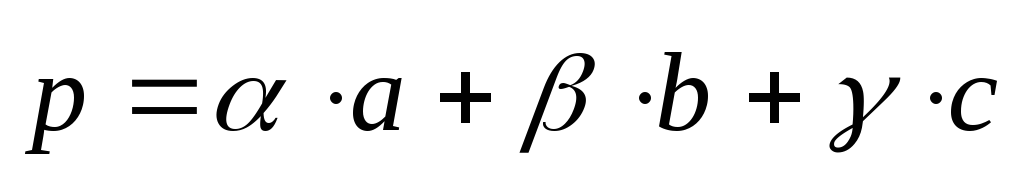 .
.
-
Докажем единственность чисел
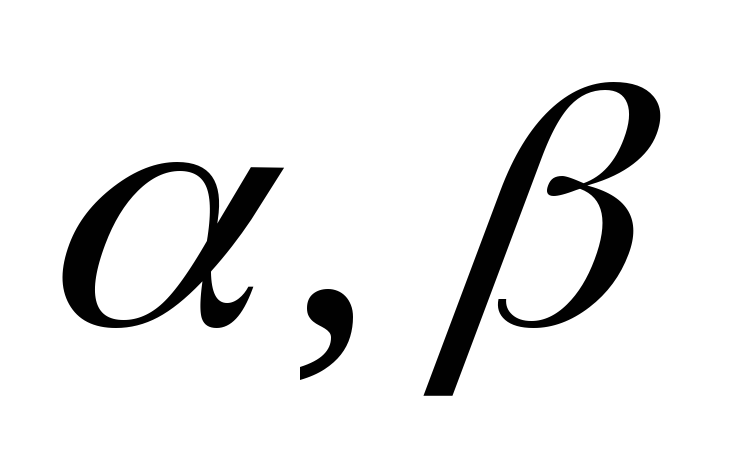 и
и
 методом от противного.
методом от противного.
Следствие 2.2. Любая система, состоящая более чем из трех векторов, линейно зависима.
Определение 2.3. Векторным
произведением двух неколлинеарных и
ненулевых векторов![]() и
и
![]() ,
взятых в определенном порядке, называется
такой вектор
,
взятых в определенном порядке, называется
такой вектор
![]() ,
что:
,
что:
-
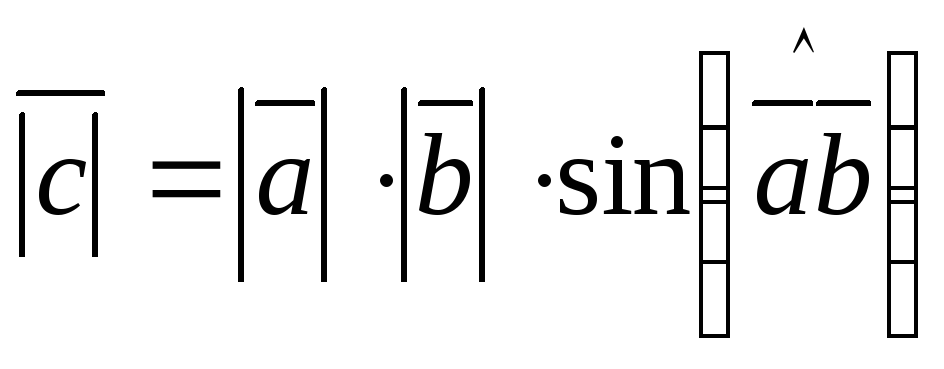 ;
; -
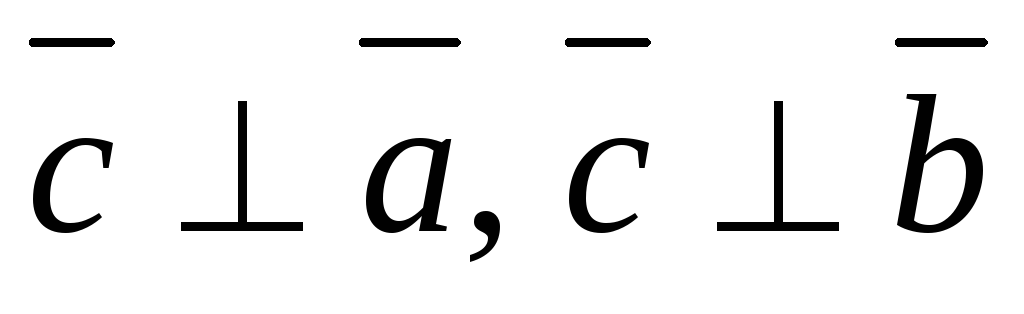 ;
; -
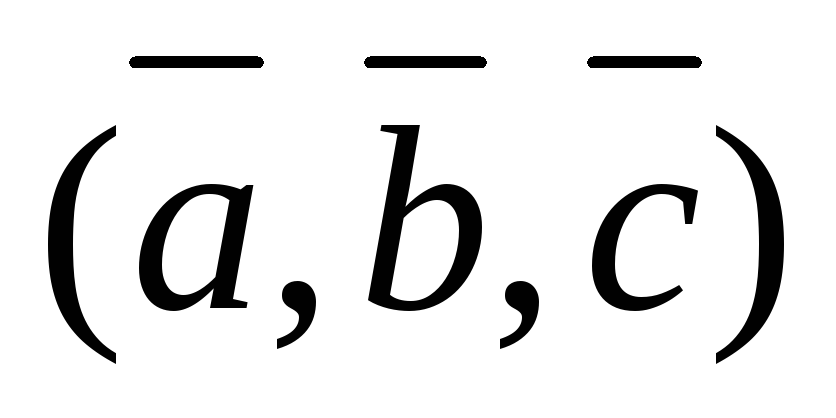 - тройка положительно ориентирована и
одинаково ориентирована с базисом, в
котором она рассматривается.
- тройка положительно ориентирована и
одинаково ориентирована с базисом, в
котором она рассматривается.
Обозначается
![]()
Свойства векторного произведения.
-
Векторное произведение векторов
 и
и
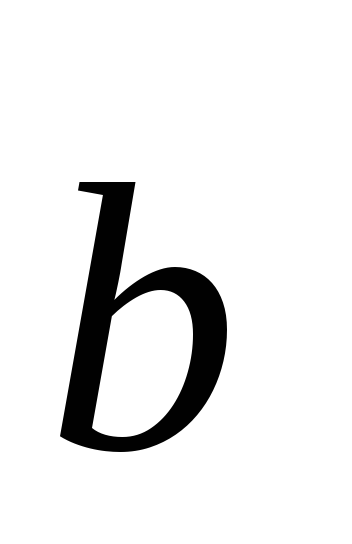 равно нулевому вектору, если один из
векторов нулевой или векторы
равно нулевому вектору, если один из
векторов нулевой или векторы
 и
и
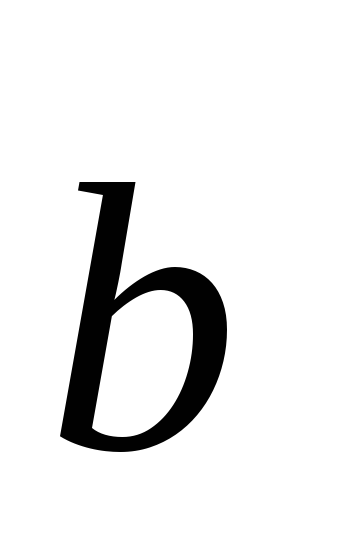 коллинеарны:
коллинеарны:
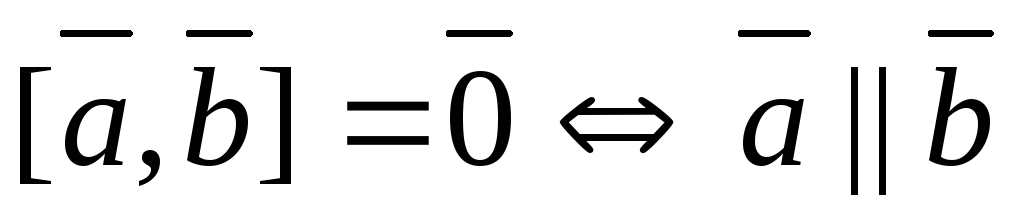 или
или

-
При перемене порядка сомножителей векторное произведение не меняет своего модуля, но меняет направление на противоположное:
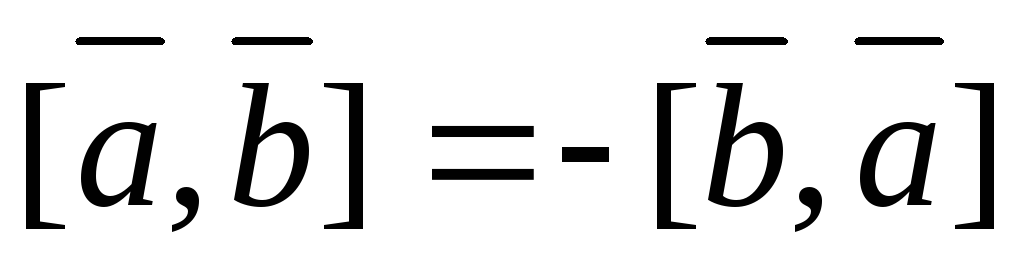
-
Сочетательное свойство векторного произведения при умножении на скаляр выражается равенством:
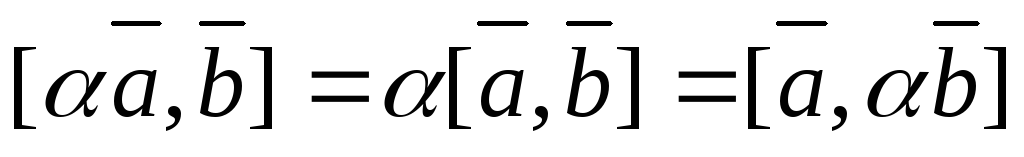
-
Распределительное свойство векторного произведения выражается равенством:
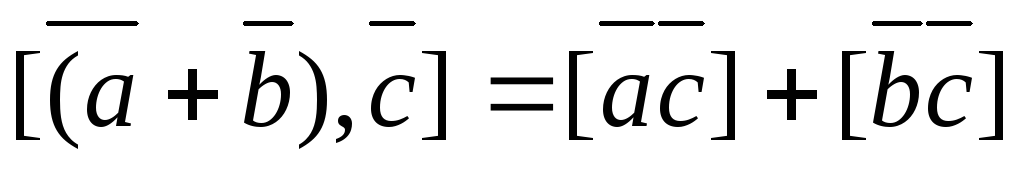
-
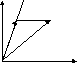
Векторное произведение не изменится, если один из сомножителей, например, вектор
 заменить его проекцией вектором
заменить его проекцией вектором
 на прямую, лежащую в плоскости векторов
на прямую, лежащую в плоскости векторов
 и
и
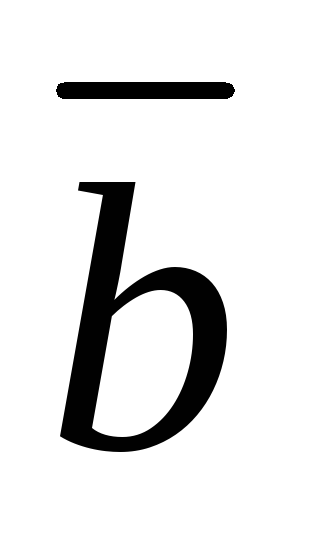 и перпендикулярную к
и перпендикулярную к
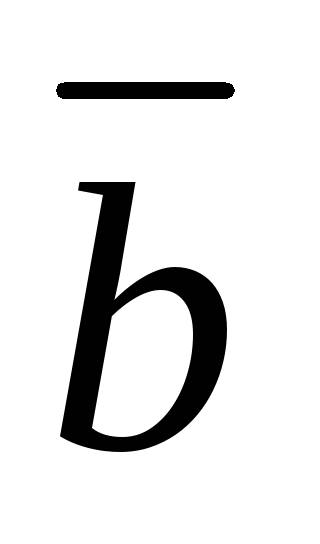 :
:
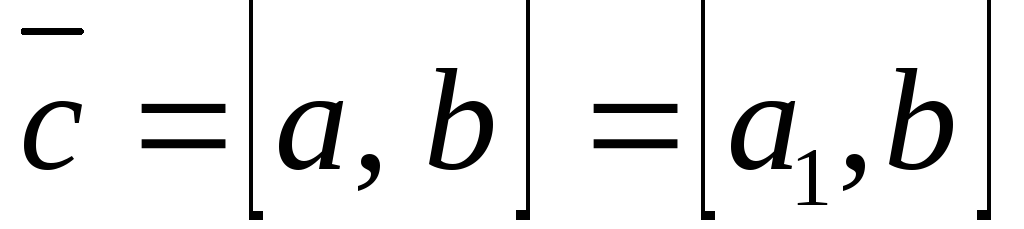
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Рассмотрим векторные произведения
единичных векторов прямоугольной
системы координат. На основании свойства
1 имеем:
![]() .
Из определения векторного произведения
следует, что
.
Из определения векторного произведения
следует, что
![]() .
.
Теорема 2.4. Если векторы
![]() и
и
![]() в ортонормированном базисе
в ортонормированном базисе
![]() имеют координаты
имеют координаты
![]() ,
то вектор
,
то вектор
![]() имеет координаты:
имеет координаты:
![]() .
.
Доказательство:
-
Разложим векторы
 и
и
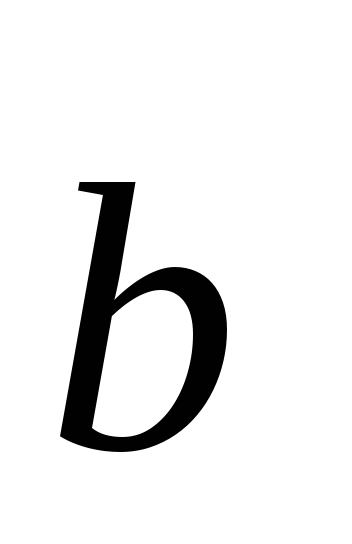 по векторам базиса
по векторам базиса
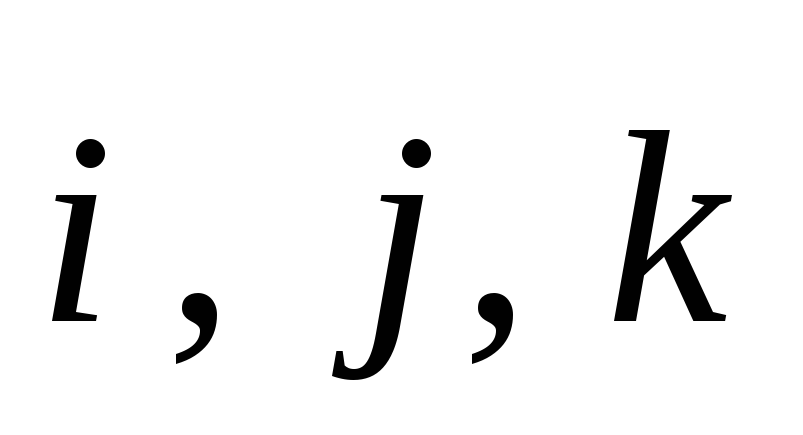 :
:
![]() ,
,
![]() .
.
-
Составим векторное произведение:
![]() [(
[(![]() ),
(
),
(![]() )]
)]
Пользуясь свойствами 2, 3, 4 векторного произведения, получим:
![]()
![]()
Последнее равенство можно записать в виде:
![]() или
или
![]()
- координаты векторного произведения
векторов
![]() и
и
![]() в положительно ориентированном базисе.
в положительно ориентированном базисе.
Координаты векторного произведения
векторов
![]() и
и
![]() в
отрицательно ориентированном базисе
-
в
отрицательно ориентированном базисе
-
![]()
Геометрический смысл векторного произведения.
Теорема 2.5. Абсолютная
величина векторного произведения
![]() равна площади параллелограмма,
построенного на этих векторах.
равна площади параллелограмма,
построенного на этих векторах.
Доказательство:
-
По определению
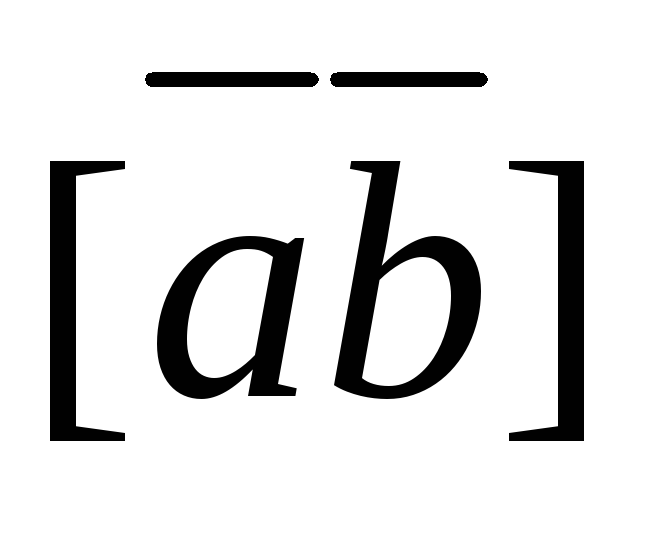 =
=
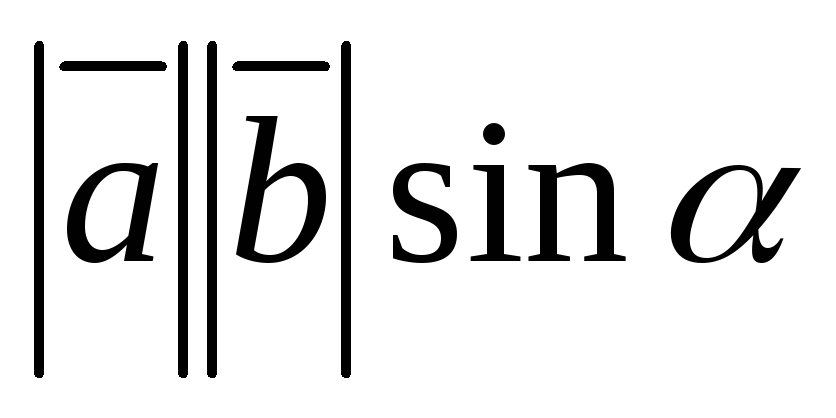
-
S параллелограмма =
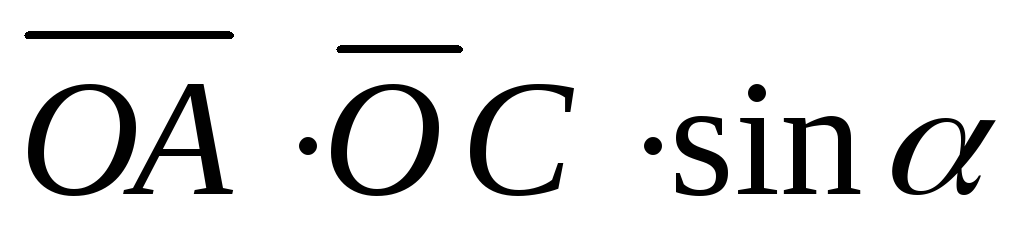
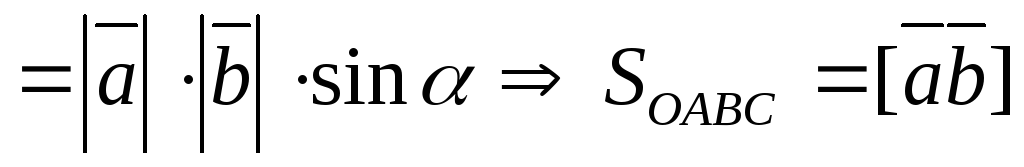
Задача 2: Вычислить площадь
и высоту параллелограмма построенного
на векторах
![]() и
и
![]()
З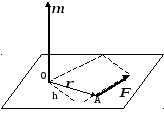 адача.3:
Найти площадь треугольника,
если известны координаты его вершин
А(1, -2, 3), В(5, 0, -1), С(1, 0, 4)
адача.3:
Найти площадь треугольника,
если известны координаты его вершин
А(1, -2, 3), В(5, 0, -1), С(1, 0, 4)
Физический смысл векторного произведения векторов
Моментом силы
![]() относительно точки
относительно точки
![]() называется вектор
называется вектор
![]() ,
имеющий начало в точке
,
имеющий начало в точке
![]() ,
направленный перпендикулярно к
плоскости, определяемой точкой и
вектором силы
,
направленный перпендикулярно к
плоскости, определяемой точкой и
вектором силы
![]() .
Длина вектора
.
Длина вектора
![]() равна произведению длины вектора
равна произведению длины вектора
![]() на плечо
на плечо
![]() (
(![]() -
длина перпендикуляра, опущенного из
точки
-
длина перпендикуляра, опущенного из
точки
![]() на направление вектора
на направление вектора
![]() ),
или
),
или
![]() ,
где
,
где
![]() - радиус-вектор точки приложения силы
- радиус-вектор точки приложения силы
![]() .
Иначе,
.
Иначе,
![]() .
.
Таким образом, вектор момента силы есть векторное произведение вектора силы и радиус-вектора точки приложения силы.
