ГОСЫ / вопрос 12 / Лекция 14-15

Лекция 14-15

Открытие неевклидовой геометрии. Система аксиом плоскости Лобачевского. Параллельные прямые по Лобачевскому и их свойства. Расходящиеся прямыеАксиоматика Лобачевского.

Треугольники и четырехугольники на плоскости Лобачевского. Угол параллельности . Окружность, эквидистанта, орицикл. Различные модели плоскости Лобачевского

Геометрия Лобачевского построена на аксиоматике Гильберта, включает в себя все четыре группы этой аксиоматики.

Пусть а произвольная прямая, А- точка не лежащая на этой прямой, тогда в плоскости, определенной точкой А и прямой а, существует не менее двух прямых, проходящих через т. А и не пересекающих прямую а.

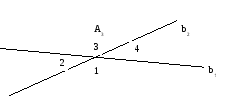
b₁ и b₂ образуют вертикальные углы 1,3 и 2,4. По аксиоме Лобачевского а не пересекает b₁ и b₂ ,а, значит все её точки принадлежат внутренней области одного из вертикальных углов, тогда очевидно, что все прямые, проходящие через точку А и лежащие внутри 2 и 4 вертикальных углов, не пересекают прямую а. В геометрии Лобачевского прямая считается направленной прямой: ОВ –предполагается что все её точки выбраны так, что они находятся меду точками А и В.

Определение: Прямая АВ называется параллельной прямой СD если эти прямые не пересекаются и каковы бы ни были точки P и Q, лежащие соответственно на прямых АВ и СD, любой внутренний луч угла QPB пересекал бы луч QD.

Свойства параллельных прямых.

1. Если прямая а параллельна прямой b в данном направлении (т.е. вправо или лево), то прямая b параллельна а в том же направлении.

2. Если прямые а и b, а║b и b║с в данном направлении, то они параллельны между собой в данном направлении.

Две прямые называются расходящимися, если они пересекаются и они не параллельны. Таким образом, через каждую точку данной прямой проходят две прямые, параллельные ей, и бесконечно много расходящихся с ней. Все они лежат внутри пары вертикальных углов, образованных параллельными прямыми.

Свойства расходящихся прямых.

1. Две прямые, параллельные третьей прямой, расходятся.

2. Две прямые, которые при пересечении с третьей образуют равные накрест лежащие или соответственные углы, расходятся

3. Всякие две расходящиеся прямые имеют единые общий перпендикуляр, по обе стороны от которого они не ограничено удаляются одна от другой.

Взаимное расположение параллельных прямых.

Определение.

Прямая а и b называется асимптотически сближающимися в данном направлении, если длина перпендикуляра опущенного из точки М прямой а на прямую b, стремится к нулю при неограниченном удалении точки М₀ от точки М в данном направлении по прямой а.

М₀

Теорема.

Две параллельные прямые асимптотически сближающиеся в сторону параллельности и неограниченно удаляются друг от друга в противоположном направлении α₀ –угол параллельности.

Угол параллельности зависит по Лобачевскому от выбора точки N прямой b. Не существует двух точек прямой b в которых углы параллельности равны. Угол параллельности в точке N по отношению к прямой, а зависит только от расстояния от точки N до прямой а. Для вычисления угла параллельности Лобачевским введена функция π и угол определяется как значение этой функции. Областью определения данной функции является интервал от 0 до бесконечности, областью значения – от 0 до π/2. Функция монотонно убывающая непрерывна на интервале от 0 до бесконечности, α₀→ π/2, если S=0, α₀→0, если S→бесконечности.

Определение.

Эквидистантой называется множество точек, расположенных по одну сторону от прямой а и удаленных от неё на данное расстояние. Прямая а называется базой эквидистанты, длина перпендикуляра, опущенного из точки эквидистанты на базу- высота эквидистанты. На евклидовой плоскости эквидистанта есть прямая, на плоскости Лобачевского это не так.

Теорема.

Ни какие три точки эквидистанты на плоскости Лобачевского не лежат на данной прямой.

ВВ₁ – высота эквидистанты

(длинна наибольшего перпендикуляра)

Теоремы.

Все точки эквидистанты лежат по одну сторону от прямой l, проходящей через её любую точку, перпендикулярное её высоте. Эта прямая является касательной к эквидистанте в точке А.

Теорема.

Для того чтобы две эквидистанты были равны необходимо и достаточно, чтобы они имели равные высоты.

Эквидистанты представляют собой ортонормированные траектории гиперболического пучка (по Лобачевскому гиперболическим пучком является множество прямых перпендикулярных данной прямой). Вводится система, которая на плоскости Лобачевского: такая, что ось х - данная прямая, ось y –одна из параллельных прямых. Такая система координат называется эквидистантой.

Рассмотрим пучок параллельных прямых в данном направлении. Пусть а - некоторая прямая этого пучка. Через точку А этой прямой проводим секущую к прямым пучка.

углы наклона

Точки, которые образуются при пересечении прямой с секущей, образуют множество точек, называемых орициклой.

Теорема.

Никакие три точки орициклы не лежат на одной прямой. Все точки орициклы лежат по одну сторону от прямой t, проходящей через любую его точку перпендикулярную к соответствующей оси. Для любых множеств параллельных прямых орициклы равны. Окружность, эквидистанта и орицикла на плоскости Лобачевского является ортогональными траекториями соответственно эллиптического, гиперболического и параболического пучков.

Дефект треугольника.

Пусть дан треугольник АВС (Т); σ(Т)- сумма углов треугольника Т.

Сумма углов треугольника не превосходит π.

Дефектом треугольника называется величина d(Т)= π- σ(Т). Если треугольник АВС разбит на два треугольника, то d(АВС)= d(АВD)+d(BDC).Пусть B₁ и С₁ произвольные точки на АВ и АС треугольника АВС. Тогда выполняется неравенство d(АВ₁С₁)≤d(АВС). Пусть у прямоугольных треугольников АВС и А₁В₁С₁ катеты ВС и АС соответственно не меньше катетов А₁С₁ и В₁С₁, тогда если сумма углов треугольника АВС равна π, то сумма углов треугольника А₁В₁С₁ равна π.