Бусыгин

31

пример, Жерар Дебре18 доказал, что функция полезности существует, если предпочтения непрерывны.

Определение 5.

Отношение , заданное на X называется непрерывным в X, если для любых сходящихся последовательностей {xn} , {yn}, таких что xn, yn X n и xn yn, выполнено x y,

где x = limn→∞ xn и где y = limn→∞yn.

Перед тем как перейти к обсуждению существования функции полезности для непрерывного отношения предпочтения докажем важную вспомогательную лемму.

Теорема 6.

Пусть на X ÊK задана система неоклассических предпочтений. Тогда следующие утверждения эквивалентны.

(1)предпочтение } – непрерывно;

(2)для любого x X множества {y X | x } y} и {z X | z } x} замкнуты в X.

(3)для любого x X множества {y X | x } y} и {z X | z } x} открыты в X.

(4)если x } y, то существуют непересекающиеся окрестности Vx и Vy точек x и y соответственно, такие, что для любых a Vx и b Vy выполнено a } b.

Доказательство:

Доказательство проведем по схеме 1 2 3 4 1.

(1) (2) Возьмем любую сходящуюся последовательность {yn}, такую, что yn {y X | x } y} и limn→∞yn = y. Для нее имеем, что для любого n выполнено x }yn. По свойству не-

прерывности имеем, что x } y, т.е. y {y X | x } y}, что и означает замкнутость множества {y X | x } y}. Замкнутость второго множества доказывается аналогично.

(2) (3) Так как дополнениями множеств {y X | x } y} и {z X | z } x} в пределах X являются множества {y X | x } y} и {z X | z } x}, то отсюда следует, что первые два множества замкнуты тогда, и только тогда, когда вторые два открыты.

(3) (4) Пусть x } y. Возможны два случая.

1)Существует элемент z X, такой, что x } z } y. Тогда открытые множества Vx={a X| a } z} и Vy ={b X| z } b}, удовлетворяют требуемым свойствам. Так, x Vx, y Vy. Покажем, что Vx]Vy= . Пусть это не так, т.е. существует некоторый элемент x′X, такой, что x′ Vx] Vy. Тогда x′ } z и z } x′ по транзитивности имеем x′ } x′. Противоречие с иррефлексифностью отношения } , значит Vx] Vy= . Читателю предлагается самостоятельно проверить, что для любых a Vx и b Vy выполнено a } b.

2)Не существует элемента z X такого, что x } z } y. В этом случае составим множества

Vx={a X| a } y} и Vy ={b X| x } b}. Эти множества открыты, и, кроме того, x Vx, y Vy. Покажем, что они не пресекаются. Пусть это не так, т.е. существует некоторый эле-

мент x′Xтакой, что x′ Vx] Vy. Тогда x′ } y и x } x′, что противоречит с исходной по-

18 Debreu, Gerard, Representation of a Preference Ordering by a Numerical Function, in Decision Theory, Thrall, Coombs, Davis, eds. Wiley, New York, 1954

31

32

сылкой, о том, что не существует элемента z X такого, что x } z } y. Читателю предлагается самостоятельно проверить, что для любых a Vx и b Vy выполнено a } b.

(4) (1) Возьмем некоторые сходящиеся последовательности {xn} , {yn}, такие что xn, yn

X n, x = limn→∞ xn , y = limn→∞yn и xn}yn. Предположим, что y } x, тогда для точек x, y найдутся окрестности Vx и Vy, такие, что для любых a Vx и b Vy выполнено b } a.

Это означает, что при достаточно больших значениях n имеем yn } xn. Что противоречит xn}yn. Таким образом, получили, что x}y.

*

Приведенные эквивалентные определения непрерывности позволяют выявить содержательный смысл понятия непрерывности: если мы явно предпочитаем один из наборов другому, то, в «малом», т.е. при рассмотрении достаточно близких наборов наша ранжировка сохранится.

В формулировке данной теоремы появились два важных множества, которые мы будем использовать в дальнейшем. Назовем, множества {z X | z } x} и {y X | x } y} верхним и нижним лебеговским множеством, соответственно, и введем для них следующие обозначения:

L+(x)= {z X | z } x} и L–(x) = {y X | x } y}.

Соответственно, непрерывность предпочтений с учетом этих терминов можно переформулировать как требование замкнутости верхнего и нижнего лебеговских множеств в X19.

Пример 3. (Продолжение)

								2
Покажем, что в случае лексикографического отношения предпочтения для любого x Ê
								+
множества {y Ê	2	| x }	L	y} и {z Ê	2	| z }	L	x} не являются ни замкнутыми, ни открытыми
	+				+
2				} мы, как и ранее, подразумеваем отношение, построенное на
в Ê . Под отношением

+

L

основе }L по правилу x }Ly !(y }L x), или

x }Ly ( (x1 > y1) или ( x1 = y1, x2 > y2)).

Изобразим теперь верхнее лебеговское множество для данного отношения }L (Рисунок 2).

x2

L+(x)

x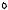

x1

19 Иногда, свойство замкнутости верхнего (нижнего) лебеговского множества называют полунепрерывностью предпочтений сверху (снизу).

32

33

Рисунок 2. Верхнее лебеговское множество для лексикографического упорядочения.

Очевидно, что изображенное на рисунке множество не является ни замкнутым, ни открытым. И, таким образом, отношение }L не является непрерывным

Теперь сформулируем и частично докажем анонсированную выше теорему Ж. Дебре о существовании функции полезности представляющей систему неоклассических предпочтений.

Теорема 7.

Пусть на X ÊK задана непрерывная система неоклассических предпочтений, тогда существует непрерывная функция полезности, представляющая эти предпочтения.

Доказательство:

Как уже говорилось, мы не будем полностью доказывать этот результат. А докажем только часть его, а именно, существование функции полезности. За доказательством непрерывности заинтересованный читатель отсылается к оригинальной работе Троута Радера20, чей вариант доказательства теоремы Дебре мы и приводим.

Рассмотрим систему открытых шаров в ÊKс рациональными центрами и радиусами. Очевидно, что таких шаров счетное число. На основании этих шаров, построим систему открытых множеств {On}+n=1∞ по следующему принципу: в эту систему попадают непустые пересечения исходной системы открытых шаров с множеством X. Обозначим через L– –(x) множество потребительских наборов из X, которые строго хуже x, т.е. L– –(x)= {y X| x} y}. Введем в рассмотрение, множество N(x)= {n| On L– –(x)}.

Покажем, что [n N(x)On= L– –(x). Так как для каждого n N(x) выполнено On L– –(x), то имеем, что [n N(x)On L– –(x).

Докажем обратное включение: L– –(x) [n N(x)On. Возьмем некоторую точку y L– –(x), в силу открытости L– –(x) она входит в L– –(x) с некоторой своей окрестностью, в которую можно вписать пересечение открытого шара в ÊKс рациональными центрами и радиусами с множеством X, причем так, что это пересечение содержит точку y. Другими словами, существует множество On, которое принадлежит этой окрестности и содержит y. Следовательно, y [n N(x)On.

Далее, каждой точке x X сопоставим величину

u(x)= Û (1)n ,

n N(x) 2

в случае если N(x)= , то положим u(x)=0.

Покажем, что определенная таким образом функция u(.) представляет нашу систему предпочтений.

Пусть x}y. Тогда по транзитивности нестрогого отношения имеем, что L– –(y) L– –(x). Откуда N(y) N(x) и соответственно u(x)> u(y).

20 Rader, Trout, The Existence of a Utility Function to Represent Preferences, Review of Economic Studies, 30(3), 1963

33

34

Пусть теперь u(x)>u(y). В силу полноты отношения } заключаем, что, либо x}y, либо y}x. Предположим, что выполнено y}x. В этом случае L– –(x) L– –(y), и при этом L– – (x)≠ L– –(y). Отсюда заключаем, что N(x) N(y) и N(x)≠N(y), а значит, по определению u(.), имеем u(x) < u(y). Получили противоречие с u(x)>u(y). Таким образом, доказано, что u(x)>u(y) влечет x}y. Тем самым, построенная функция u(.), является функцией полезности для исходной системы неоклассических предпочтений. *

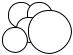
Данный вариант доказательства имеет достаточно ясную графическую интерпретацию (см. Рис 3). Мы заполняем нижнее лебеговское множество открытыми «шариками» с рациональными радиусами и центрами, и, фактически, в качестве функции полезности берем нечто сходное по духу с площадь нижнего лебеговского множества.

x2

L+i (x)

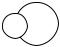
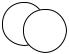
x1

Рисунок 3. Построение функции полезности по схеме Радера.

Еще одно элегантное доказательство теоремы Дебре с выразительной графической интерпретацией можно построить при довольно естественном предположении о монотонности

предпочтений.

Достаточно разумно потребовать, чтобы полезность индивидуума возрастала при росте количества потребляемых благ, т.е. потребитель предпочитал большее количество блага меньшему.

Определение 6.

(1)Отношение предпочтения } на X называется монотонным, если x, y X из x > y следует x } y.

(2)Отношение предпочтения называется строго монотонным, если из x >y и x ≠ y следует x } y.

При этом дополнительном предположении докажем следующий ослабленный вариант теоремы Дебре.

Теорема 8.

Пусть на X=ÊK+ заданы непрерывные, строго монотонные предпочтения. Тогда сущест-

вует непрерывная, строго монотонная функция полезности представляющая эти предпочтения.

Доказательство:

В качестве функции полезности можно взять соответствие, которое сопоставляет каждому

x ÊK такое число u(x), что x u(x)1, где 1 — K-мерный вектор, состоящий из единиц.

+

34

35

Покажем, что такое число u(x) всегда существует и единственно. (См. Рисунок 4 для иллюстрации идеи доказательства)

x2
x
u(x)1	u3
	u2
	u1
	x1

Рисунок 4. Построение функции полезности при предположении монотонности предпочтений (u1< u2< u3).

Для этого мы должны найти для каждого набора x эквивалентный ему набор из множества U = {u1 | u Ê+}, которое является лучом, выходящим из начала координат. Сопоставим рассматриваемому набору x множество чисел u, соответствующих не худшим наборам из

U

U +(x) = {u Ê+ | u1}x}

и множество чисел u, соответствующих не лучшим наборам из U

U –(x) = {u Ê+ | x } u1}.

Эти множества не пусты, так как из свойства строгой монотонности следует, что 0 U – (x) и max{xk}+1 U +(x).

Множество U +(x) лежит выше U –(x) поскольку из строгой монотонности следует, что u1 U –(x) и u2 U +(x) выполнено u1< u2.

Обозначим u+ = inf U +(x) и u– = sup U –(x). Эти величины конечны, так как множества U – (x) и U +(x) ограничены сверху и снизу соответственно. По непрерывности предпочтений u+ U +(x) и u– U –(x). При этом u+ > u–. Покажем, что u+ =u–. Пусть это не так. Тогда существует число u′ такое, что u– < u′ < u+, так что u′ U –(x) и u′ U +(x). Это противоречит

полноте предпочтений, так как, по свойству полноты мы должны иметь либо u′ 1} x, либо u′1 { x.

Полученная точка u = u+ = u– удовлетворяет требуемому условию x u1 и единственна.

Заданная таким образом функция u(x) является функцией полезности. Пусть x1 } x2. По построению x1 u(x1)1 и x2 u(x2)1. Значит, x1 } x2 тогда и только тогда, когда u(x1)1 } u(x2)1. Но из строгой монотонности u(x1)1 } u(x2)1 тогда и только тогда, когда u(x1)> u(x2).

Функция полезности u(x) является строго монотонной. Пусть x1 > x2 и x1≠x2. Тогда из строгой монотонности предпочтений x1 } x2. Отсюда следует, что u(x1)1 } u(x2)1. По-

этому u(x1) > u(x2).

35

{u(xn)}n∞=N+1

{u(xn)}n∞=N+1

36

Докажем теперь непрерывность функции полезности u(x). Для доказательства непрерывности функции полезности рассмотрим последовательность {xn}∞n=1 такую, что limn → ∞ xn = x. Нам надо показать, что limn → ∞ u(xn) = u(x). Зафиксируем некоторое число ε> 0. Заметим, что можно выбрать u и -u такие, что для любого вектора y из ε-окрестности точки x (т.е. || y – x || < ε) выполнено

u1 Á y Á -u 1.

Например, можно взять u = mink{xk} – 2ε и -u = maxk{xk} + 2ε. Как нетрудно заметить, по строгой монотонности мы имеем u < u(y) < -u. Для любой сходящейся подпоследователь-

ности из {xn}n∞=1 найдется достаточно большое число N, такое, что при n > N имеем || xn – x|| < ε, т.е. последовательность, начиная с номера N+1, попадает в ε-окрестность точки x. Тогда, как мы показали выше, u(xn) попадает в интервал [u ,u-].

Покажем теперь, что любая сходящаяся подпоследовательность из последовательности сходится к одному и тому же числу u(x). (Отметим, что, так как бесконечная

последовательность {u(xn)}n∞=N+1 задана на компакте [u ,u-], то она должна иметь точки сгущения. Мы хотим показать, что существует всего одна точка сгущения и это u(x).)

Рассмотрим теперь некоторую сходящуюся подпоследовательность {u(xnk)}k=1∞ из

. Пусть эта последовательность сходится к u~ и при этом u~ ≠ u(x). Предположим что u~ >u(x). Возьмем некоторое число u^, такое что u~ > u^ > u(x). По свойству стро-

гой монотонности имеем, что u^1 } u(x)1. Поскольку {u(xnk)}k=1∞ сходится к u~, то существует M такое, что при k > M выполнено u(xnk) > u^. По определению функции полезности

xnk ~ u(xnk)1 и, кроме того, по строгой монотонности u(xnk)1 } u^1 ( k > M), т.е. xnk ~ u(xnk)1} u^1. Так как предпочтения непрерывны, то x } u^1, но x ~ u(x)1, поэтому u(x)1 } u^1. Однако выше было показано, что u^1} u(x)1. Получили противоречие и тем самым доказали непрерывность построенной функции полезности.

*

Как видно из приведенных выше вариантов теоремы существования функции полезности, требование непрерывности достаточно сильно, так как помимо существования функции полезности мы получаем еще и дополнительное свойство ее непрерывность. Но, с другой стороны, непрерывность функции полезности свойство, значение которого трудно переоценить. Его наличие автоматически21 дает нам существование функции спроса потребителя в большинстве задач, которые будут нас интересовать.

В заключение данного раздела остановимся на вопросе о нетранзитивных предпочтениях. Как обсуждалось выше, условие транзитивности является ограничительным при моделировании поведения потребителя. Поэтому, вполне естественным задаваться вопросом о свойствах предпочтений и о существовании функции полезности в случае, если строгое отношение предпочтения } не обладает свойством отрицательной транзитивности, или, что эквивалентно, что отношение нестрогого отношения предпочтения } не обладает свойством транзитивности. Естественно, как показывает приведенная выше Теорема 4, при отсутствии предположения транзитивности функции полезности в смысле Определения 4 не существует, но, тем не менее, даже в этом случае, можно построить некоторый

21 Вспомните о теореме Вейерштрасса.

36

37

индикатор полезности заданный на парах альтернатив упорядочивающий потребительские наборы тем же образом, что и отношение предпочтения.

Теорема 9.

Пусть на X ÊK задано полное отношение предпочтения } и, кроме того, } замкнуто в Ê K× ÊK. Тогда существует непрерывная функция k: X× X→Ê такая, что

(1)k(x, y) > 0 тогда и только тогда, когда x } y;

(2)k(x, y) < 0 тогда и только тогда, когда y } x;

(3)k(x, y) = 0 тогда и только тогда, когда x ~ y;

(4)k(x, y) = – k(y,x).

Доказательство:

Пусть }–1 – множество, задаваемое по правилу

}–1={(x, y) X× X | (y, x) }}.

Определим множество безразличия I = } ] }–1 на X. Отметим, что в силу полноты отношения } это множество непусто (Почему?). Далее, для любой пары (x, y) X× X определим функцию

d′(x, y)=inf(x′, y′) I d((x, y), (x′, y′)),

где d(x, y) – евклидово расстояние на ÊK× ÊK. Теперь покажем, что так определенная функция является непрерывной. Для любой пары x~, y~ X× X и z~ I в силу неравенства треугольника имеем d(x~,z~) < d(x~,y~) + d(y~,z~). Следовательно,

inf z~ I d(x~,z~) < d(x~,y~) + d(y~,z~).

Так как сейчас левая часть выражения не зависит от z~, то

inf z~ I d(x~,z~) < d(x~,y~) + inf z~ I d(y~,z~).

Аналогично получаем

inf z~ I d(y~,z~) < d(x~,y~) + inf z~ I d(x~,z~).

Комбинируя два последних неравенства, находим

| inf z~ I d(y~,z~) – inf z~ I d(x~,z~)| < d(x~,y~),

что и означает непрерывность функции d′(x, y).

Далее положим k(x, y) = d′(x, y), если x } y и k(x, y) = - d′(y, x), если y } x. Теперь покажем, что так определенная функция удовлетворяет условиям теоремы.

(1 ) Пусть k(x, y) > 0. Тогда в силу d′(x, y)>0 и определения величины k(x, y) имеем, что x } y. Очевидно, что x~y (т.е. (x,y) I) быть не может, так как в этом случае d′(x, y)=0, а значит и k(x, y)=0. Таким образом, x } y.

(1 ) Пусть нашлись x, y X такие, что x } y. В силу замкнутости отношения } в ÊK× ÊK , имеем, что I замкнутое множество в ÊK× ÊK. Следовательно, дополнение к I множество открытое, и, значит, найдется ε–окрестность точки (x, y), содержащаяся в этом дополнении. По определению k(.,.) это означает, что k(x, y) > ε > 0.

37

38

(2)Доказательство пункта 2 аналогично приведенному выше.

(3)Доказательство данного пункта оставляется читателю в качестве упражнения.

(4)Свойство k(x, y) = – k(y,x) выполнено по построению функции k(. , .).

*

Так построенная функция может считаться обобщенной функцией полезности представляющей отношение предпочтения }. В отличие от ранее определенной функции полезности u(.), функция k(.,.) не сопоставляет числовое значение альтернативе из X, а лишь указывает для каждой пары альтернатив из X наиболее предпочтительную. Отметим, однако, что если предпочтения представимы функцией полезности u(.), то в качестве k(x, y) можно взять функцию u(x) – u(y). Очевидно, что если в качестве базового индикатора полезности взять функцию k(x, y), то возможно систематическое построение микроэкономической теории на основе нетранзитивных предпочтений.22

В дальнейших параграфах мы больше не будем касаться случая нетранзитивных предпочтений и рассмотрим вариант теории, где за основу взята система неоклассических предпочтений, т.е. тех, где строгое отношение удовлетворяет свойствам асимметричности и отрицательной транзитивности, а нестрогое отношение предпочтения свойствам полноты и транзитивности.

Задачи

22.Алина Александровна Алексашенко предложила следующее определение функции полезности: Будем называть u(.): X→Ê функцией полезности потребителя, соответствующей системе неоклассических предпочтения {}, }, ~}, если для всякой пары альтернатив x, y X отношение x}y верно тогда и только тогда, когда u(x) > u(y). Будет ли оно эквивалентно определению, приведенному в тексте? Ответ аргументируйте.

23.Покажите, что суперпозиция строго возрастающей функции и функции полезности, представляющей некоторое отношение предпочтения }, также является функцией полезности, представляющей это отношение предпочтения. Какие из нижеприведенных функций могут выступать в качестве такого преобразования?

a) f(x)=x2; b) f(x) = x3+x; c) f(x)= x;

d) f(x)= ex.

Приведите пример, показывающий, что требование строгого возрастания не может быть ослаблено до возрастания.

24. Пусть } — полное и транзитивное бинарное отношение, заданное на множестве X. Для каких из нижеприведенных множеств X это отношение может быть представлено некоторой функцией полезности?

a)X={x Ên| xi — целые числа};

b)X={x Ên| 0 <xi<1};

c)X=Ên;

d)X=Ên+ ;

e)X={x Ên| xi — иррациональные числа};

22 Смотри, например, Wayne J. Shafer, The Nontransitive Consumer, Econometrica, 42(5), 1974

38

39

f)X={x Ên| xi =a 2 + b 3, где a и b любые рациональные числа}.

25.Покажите, что если система неоклассических предпочтений задана на конечном множестве альтернатив, то в этом множестве существует, как наименьший, так и наибольший элемент.

26.В теореме 5 докажите, что построенная функция является функцией полезности.

27.Пусть допустимое множество альтернатив состоит из 4 альтернатив X={a, b, c, d}. На этом множестве задано следующее отношение предпочтения: }={( a, d), (b, d), (d, c), (b, a), (a, c), (b, c)}. Можете ли вы построить функцию полезности представляющую данные предпочтения? Если нет, то почему? Если да, то постройте.

28.Борис Бенедиктович Бахвалин на основании полного, транзитивного и непрерывного отношения предпочтения построил следующую функцию полезности:

2
x1x2, если x1+x2< 1		.
u(x1, x2)= 2	иначе
x1x2+15,

Покажите, что эта функция не является непрерывной. Нет ли здесь противоречия с непрерывностью предпочтений? Возможно ли на основании этих же предпочтений построить непрерывную функцию? Если да, то постройте ее, если нет, то поясните, почему построение невозможно.

29. Пусть X– множество альтернатив, на котором задано полное и транзитивное бинарное отношение }. Докажите, что если множество кривых безразличия счетно, то существует функция полезности представляющая }.

30. Покажите, что если функция полезности u(x) непрерывна, то нестрогое отношение предпочтения }, породившее эту функцию, также является непрерывным.

31. Закончите доказательство теоремы 6, показав, что для построенных окрестностей Vx и Vy, справедливо, что для любых a Vx и b Vy выполнено a } b.

32. Пусть X= X1× X2, где X1={1, 2,...}, а X2 — множество всех рациональных чисел между 0 и 1. Пусть на парах из X введено лексикографическое упорядочение. Докажите, что существует функция полезности, отвечающая этому упорядочению. Запишите ее явную формулу.

33. Рассмотрите следующие отношения R, заданные на Ê2++: a) (x1,x2) R(y1, y2) (x1 – x2)(y1 – y2) > 0;

x1	x2
b) (x1,x2) R(y1, y2) y1	> y2;

39

40

c)(x1,x2) R(y1, y2) x1x2 > y1 y2;

d)(x1,x2) R(y1, y2) min{x1 + x2, y1 + y2} >0;

e)(x1,x2) R(y1, y2) min{x1, x2}– min{y1, y2}>0;

f)(x1,x2) R(y1, y2) x1x2> min{ y1, y2}.

Какие из них представимы функцией полезности? Попытайтесь записать явную форму этой функции полезности.

34.Пусть X состоит из n-мерных векторов с неотрицательными компонентами, а отношение задано следующим образом: x}y, если все компоненты вектора x не меньше соответствующих компонент вектора y. Существует ли функция полезности, представляющая это предпочтение?

35.Покажите, что функция полезности монотонна тогда и только тогда, когда монотонно представляемое ею отношение предпочтения.

36.Дайте графическую иллюстрацию идеи доказательства Теоремы 9.

37.Докажите пункт 3 Теоремы 9.

Свойства предпочтений и функции полезности

При анализе конкретных микроэкономических задач часто возникает необходимость делать дополнительные предположения о предпочтениях или о функциях полезности. В данном параграфе мы обсудим наиболее часто используемые предположения о свойствах предпочтений и покажем их связь с соответствующими свойствами функции полезности, которую эти предпочтения порождают.

В предыдущем параграфе мы уже дали определение ряда важных свойств предпочтений, а именно, монотонности и строгой монотонности. Иногда, в ситуациях, когда выполнение этих свойств выглядит ограничительным, предполагается выполнение более слабого свойства – локальной ненасыщаемости. Выполнение этого свойства часто оказывается достаточным для доказательства тех свойств выбора, которые следуют из строгой монотонности предпочтений.

Определение 7.

Предпочтения называются локально ненасыщаемыми, если для любого допустимого набора x X в любой его окрестности найдется другой допустимый набор x^ X, такой что x^ } x.

Отметим, что выполнение свойства локальной ненасыщаемости запрещает два типа предпочтений:

•предпочтений c точкой насыщения, т.е. с точкой, для которой потребительский набор ей отвечающий является наилучшим выбором потребителя среди всех ближайших наборов;

40