MathAn / !Лекция_II_№10(2014-15)_St_n

Математический анализ. Модуль-4

Лекция №10 Дифференциальные уравнения 2-го порядка

1. Основные понятия

Def 1. Дифференциальным уравнением 2-го порядка (ДУ-2) называется уравнение вида

		0	,	(1.1)
F x, y, y , y

связывающее независимую переменную x , искомую функцию y y x , и ее

производные			.
	y , y
или в виде, разрешенном относительно производной y
			y	f x, y, y	(1.2)

Аналогично ДУ-1 можно дать следующие определения.

Def 2. Решением ДУ-2 называется функция y x , x a,b , которая при подстановке в уравнение (1.1) или (1.2) обращает его в тождество.

! Задача нахождения решения ДУ-2 (1.2), удовлетворяющего начальным условиям

y

y0 , y

(2)

y0 ,

называется задачей Коши.

x x0

x x0

Def 3. Общим решением ДУ-2 в некоторой области G называется функция

y x,С1,C2 , зависящая от

x и произвольных констант С1,C2 , если она является

решением ДУ при любых значениях постоянных С1,C2 , и если при любых

начальных условиях y

y0 , y

G , существуют

y0

: x0 , y0 , y0

x x0

x x0

единственные значения С1 C10,С2

C20 : y x,С10,С20 удовлетворяет данным

начальным условиям.

Def 3.1. Частным решением ДУ-2 y f x, y, y в некоторой области G

называется любая функция y x,С10,С20 , получающаяся из общего решения y x,С1,C2 этого уравнения при определенных значениях постоянных

С1 C10,С2 C20 .

1

Математический анализ. Модуль-4

Пояснение

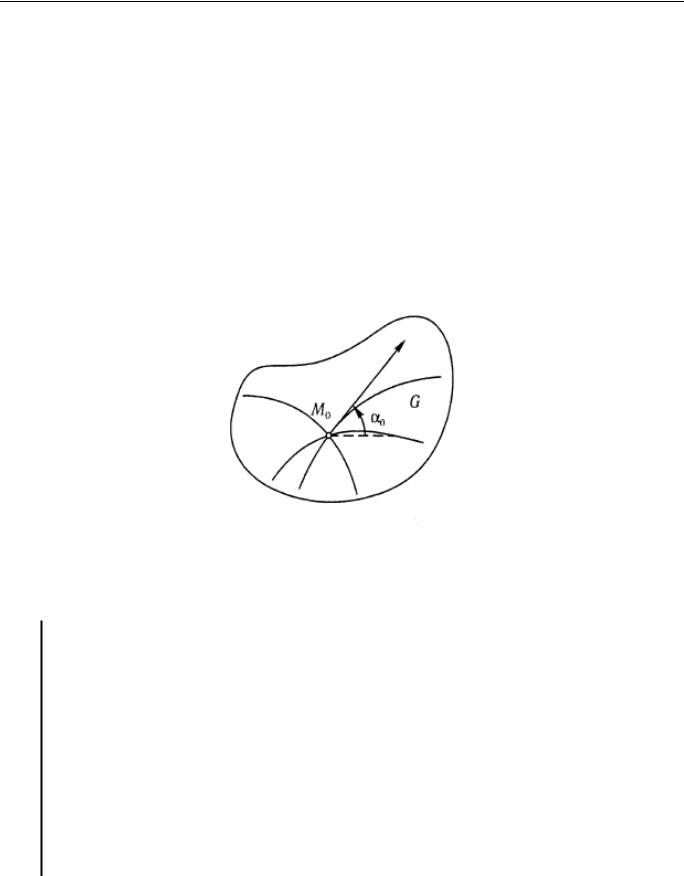
Т.к. общее решение содержит две произвольные постоянные С1,C2 , то геометрически через данную точку M 0 x0 , y0 плоскости xOy проходит пучок интегральных кривых (одна постоянная остается неопределенной).

Выделим конкретную интегральную кривую из пучка интегральных кривых. Для этого зададим направление касательной в точке M 0 x0 , y0 к искомой интегральной кривой

		tg 0		,
			y0
получим начальные условия (2): y		y0 ,		y
							y0 .
		x x0					x x0

Таким образом, решить задачу Коши (геометрически) означает, найти интегральную кривую уравнения (1.2), проходящую через заданную точку M 0 x0 , y0 в заданном

направлении tg 0
	y0 .

Теорема Коши (существования и единственности решения ДУ)

Если функция f x, y, y определена и непрерывна некоторой области G
пространства переменных x, y, y и имеет в G непрерывные ограниченные
				,					, то какова бы ни была
частные производные f y x, y, y					f y x, y, y
	G , в некоторой окрестности точки x0
внутренняя точка x0 , y0 , y0
существует единственное решение уравнения y f x, y, y ,
удовлетворяющее условиям:
	y				y0 , y
									y0 .
			x x0					x x0

! Условия (2) можно задать иначе:

Пусть требуется найти решение уравнения (1.2) на отрезке x a,b , тогда для нахождения произвольных констант С1,C2 можно задать

2

Математический анализ. Модуль-4

y		ya , y	yb	(3)
	x x0		x x0

! В этом случае задача называется краевой, а условия (4) –граничными.

2. ДУ-2, допускающие понижение порядка

Тип I. ДУ-2 вида

y f x .

(4)

Дифференцируя его дважды, получим общее решение

y f x dxdx C1x C2 .

Пример 1

Решить уравнение y 1x .

Решение

y

dx

C1 ln

x

C1,

x

~

y ln

dx C1x C2 x ln

x C1x C2 x ln

x

x

x

C1x C2 .

Ответ: y x ln

~

x

C1x C2

- общее решение.

Тип II. ДУ-2, не содержащее искомую функцию y

y f x, y .

(5)

Введем замену переменной

p , y

dp

y

dx

p

(5) примет вид ДУ-1

p f x, p .

Пример 2

Решить уравнение 1 x2 y 2xy 0 .

Решение

Замена y p , где p p x , y p 1 x2 p 2xp 0 - УРП.

3

Математический анализ. Модуль-4

dp

2xdx

p C

1 x2

.

ln

p

ln

1 x2

ln

C

p

1 x2

1

1

C1 1 x

2

y C1 1 x

2

x

3

y

C2 .

dx C1 x

3

		x	3
Ответ: y C	x				C		- общее решение.
						2
1		3

Тип III. ДУ-2, не содержащее независимую переменную x

y f y, y .

(6)

Замена

y p , где p p y

dp

dp dy

dp

y

dx

dy dx

p dy

(6) примет вид ДУ-1

p dpdy f y, p .

Пример 3.1

Решить уравнение 1 y 2 2 yy .

Решение

Замена

y p , где p p y ,

y pp 1 p2

2 ypp - УРП,

2 p dp

dy

ln

ln

ln

1 p2

y

C

,

1 p2

y

1

1 p2 C1 y , p

C1 y 1

y

C1 y 1

,

dy

dx

2

C y 1

C12

x C

2

C y 1 x C

2

2

C1 y 1

C1

1

1

4

4

										Математический анализ. Модуль-4
	C 2	x C		2	2	4
y	1								.
			4C1
			C 2	x C			2		2	4
Ответ: y			1								- общее решение.
						4C1

Пример 3.2

Решить уравнение y y 2 y , удовлетворяющее начальным условиям

y 14 , y 12 при x 1.

Решение

Уравнение относится к типу III (ДУ-2, не содержащее независимую переменную x ).

y f y, y .

Выполняем замену переменной

y p , y p dpdy , p dpdy p2 y (*)

dpdy p y p 1 - уравнение Бернулли.

По правилам делим обе части уравнения на p 1 , возвращаемся к (*).

	Замена	p2 z , 2 p	dp		dz	, откуда	1 dz			z y
			dy		dy		2 dy

или dydz 2z 2 y - ЛНДУ-1.

Решаем ЛНДУ-1

Общее решение ЛОДУ-1: z Сe 2dy Ce2 y .

Ищем общее решение ЛНДУ-1 методом вариации произвольной постоянной: z C y e2 y .

z C e2 y 2Ce2 y C e2 y 2Ce2 y 2Ce2 y 2 y ,

5

Математический анализ. Модуль-4

					1
	C 2 ye 2 y , C 2 ye 2 y dy по			частям e 2 y y			C1
					2
	z y	1	C e2 y - общее решение ЛНДУ-1.
		2	1

Последовательно возвращаемся к исходной переменной (сначала к p, затем - к y) p2 y 12 C1e2 y .

Решаем задачу Коши, подставляя начальные условия

	1		1		1	C e 2	1
								С 0
							4
	4	4			2	1		1

p2 y 2 y 12 .

																1
	Откуда						y									y 2 .
																																	1
	В окрестности начальной точки y																									0 y							y 2 - УРП.
			dy					dx							, 2 y								1	x C2 .
			y		1										2
			2
	C2		находим из начальных условий: y																								1		при x 1.
																											4
	2						1					1		1 C2 , C2 0 .
							4					2
																											y				x2			1
	Ответ:						2					y				1		x - частный интеграл;																		- частное решение. #
															2															4			2

6