73

Модуль 4. Множественная линейная регрессия

4.1.1. Общая линейная модель множественной регрессии

Значения экономических переменных определяются обычно влиянием не одного, а нескольких объясняющих факторов. В таком случае зависимость y=f(x) означает, чтох -вектор, содержащийт компонентов:х=(х₁,х₂, ... ,х_m).Задача оценки статистической взаимосвязи переменныхуих=(х₁,х₂, ... ,х_m)формулируется аналогично случаю парной регрессии. Записывается функцияу = f(,х)+,где- вектор параметров,- случайная ошибка. Предполагается, что эта функция связывает переменнуюу свектором независимых переменныххдля данных генеральной совокупности. Как и в случае парной регрессии, предполагается, что ошибки_iявляются случайными величинами с нулевым математическим ожиданием и постоянной дисперсией;_iи_jстатистически независимы приij. Кроме того, для проверки статистической значимости оценокобычно предполагается, что ошибки_iнормально распределены. По данным наблюдений выборки размерностиnтребуется оценить значения параметров,то есть провести параметризацию выбранной формулы (спецификации) зависимости.

Мы будем говорить о линейной зависимости уотх,то есть о множественной линейной регрессии. Теоретическое уравнение регрессии имеет вид:

у = ₀+₁х₁ +₂х₂ + ... +_mх_m + .

Здесь - вектор неизвестных параметров размерности(т+ 1). Пусть имеетсяпнаблюдений векторахи зависимой переменнойу. Для того, чтобы формально можно было решить задачу, то есть найти некоторый наилучший вектор параметров, должно бытьп  т+1.Если это условие не выполняется, то можно найти бесконечно много разных векторов коэффициентов, при которых линейная формула связывает между собойхиу для имеющихся наблюдений абсолютно точно. Если, в частном случае,п = т+1(например, при двух объясняющих переменных в уравненииу =₀+₁х₁+₂х₂и трех наблюдениях), то оценки коэффициентоврассчитываются един­ственным образом - путем решения системы линейных уравнений {y_j=₀+₁х_1j+₂х_2j+… +_mх_mj;j=1,2,...,п -индекс наблюдения}. Так, через три точки-наблюдения в трехмерном пространстве можно про­вести единственную плоскость, определяемую параметрами₀,₁,₂. Если число наблюдений больше минимально необходимого, то естьп > т+1,то уже нельзя подобрать линейную формулу, в точности удовлетворяющую всем наблюдениям, и возникает необходимость оптимизации, то есть выбора наилучшей формулы-приближения для имеющихся наблюдений.Положительная разность (п-т-1) в этом случае называется числом степеней свободы. Если число степеней свободы мало, то статистическая надежность оцениваемой формулы невысока. Так, если проведена плоскость "в точности" через имеющиеся три точки наблюдений, любая четвертая точка-наблюдение из той же генеральной совокупности будет практически наверняка лежать вне этой плоскости, возможно - достаточно далеко от нее. Обычно при оценке множественной регрессии для обеспечения ста­тистической надежности требуется, чтобы число наблюдений, по крайней мере, в 3 раза превосходило число оцениваемых параметров.

Задача построения множественной линейной регрессиисостоит в нахождении (m+1)-мерного вектора а, элементы которого есть оценки соответствующих элементов вектора. Критерии оценивания, как и в случае парной регрессии, могут быть различными; мы будем вновь использовать метод наименьших квадратов (МНК). Уравнение регрессии с оцененными параметрами имеет вид

у = a₀+a₁х₁ +a₂х₂ + ... +a_mх_m + e,

и критерием для нахождения вектора (а)является.

Оцененное уравнение должно описать как общий тренд (тенденцию) изменения зависимой переменной у,так и отклонения от этого тренда. Проблема здесь состоит не только в том, чтобы объяснить возможно большую долю колебаний переменнойу,но и отделить влияние каждого из факторов, рассматриваемых как объясняющие переменные.

При выполнении предпосылок 1)-4) относительно ошибок е_i(см.3.3) оценки параметров множественной линейной регрессии являются несмещенными, состоятельными и эффективными. Отклонение зависимой переменнойувj-м наблюдении от линии регрессии,е_j, записывается следующим образом:

е_j= у_j - a₀-a₁х_j1 -a₂х_j2 - ... -a_jmх_m

Обозначим сумму квадратов этих величин, которую нужно минимизировать в соответствии с методом наименьших квадратов, через Q:

Минимизируемая функция Q является квадратичной относительно неизвестных величин a_i. Необходимым условием ее минимума является равенство нулю всех ее частных производных поa_i.Частные производные квадратичной функции являются линейными функциями, и, приравнивая их всех к нулю, мы получим систему из (m+1) линейных уравнений с(т+1)неизвестными. Такая система имеет обычно единственное решение (за исключением особого случая, когда столбцы ее линейно зависимы и решения нет или их бесконечно много; однако данные реальных статистических наблюдений к такому особому случаю, вообще говоря, никогда не приводят). Данная система называется системой нормальных уравнений. Ее решение в явном виде удобнее всего выписать в векторно-матричной форме, иначе оно становится слишком громоздким. Векторно-матричная запись и вывод решения системы нормальных уравнений приведены в 4.1.2; при начальном ознакомлении с проблемой оно может быть опущено.

Для анализа статистической значимости полученных коэффициентов множественной линейной регрессии необходимо, как и в случае парной регрессии, оценить дисперсию и стандартные отклонения коэффициентов a_j.

В случае парной регрессии

В общем случае 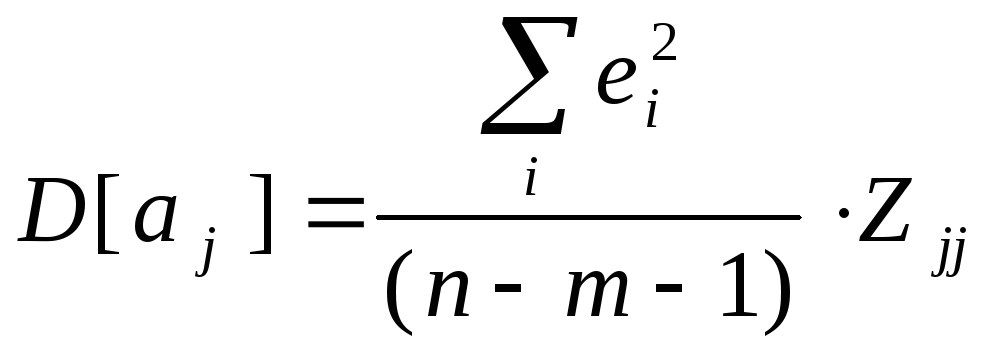(гдеZjj- диагональный элемент

матрицы (X^TX)^-1- см.4.1.2). Соответственно, стандартное отклонение, и для проверки нулевой гипотезы для каждого из коэффициентовa_jрассчитываются, как и в случае парной регрессии,t-статистики:, имеющие распределение Стьюдента с(п-т-1)степенями свободы.

Если (п-т-1),то есть число степеней свободы, достаточно велико (не менее 8 - 10), то при 5%-ном уровне значимости и двусторонней альтернативной гипотезе критическое значение t-статистики приблизительно равно двум. Здесь, как и в случае парной регрессии, можно приближенно считать оценку незначимой, еслиt-статистика по модулю меньше единицы, и весьма надежной, если модульt-статистики больше трех. Другие критерии качества полученного уравнения регрессии будут рассмотрены ниже.