econometrika / econometrika / Модуль7

96

Модуль 7. Прогнозирование

Прогнозирование в регрессионном анализе – одна из важнейших задач моделирования. Прогнозирование может использоваться для предсказания состояния системы в будущем (экстраполяция) или для оценки значения зависимой переменной от некоторого набора независимых, которых нет в исходных наблюдениях (интерполяция). Различают точечное и интервальное прогнозирование. При точечном прогнозе оценкой зависимой переменной будет число, при интервальном – оценкой будет интервал, в котором истинное значение зависимой переменной находится с заданным уровнем вероятности. Для прогноза существенно, являются ли объясняющие переменные и параметры точными значениями или приближенными, имеется ли автокорреляция.

7.1. Прогнозирование в линейной классической модели

Рассмотрим классическую регрессионную модель Y=X + , M[]=0, D[]=²E_n. Здесь Y=(y₁,y₂, … , y_n) – значения объясняемой переменной в n наблюдениях.

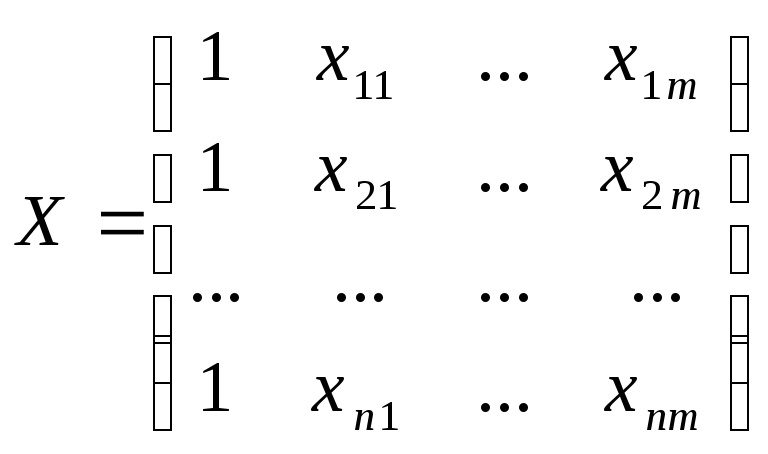- матрица значений m объясняющих переменных в n наблюдениях.

Предположим, что точке X_n+1=(x_n+1⁽¹⁾, x_n+1⁽²⁾, … x_n+1^(m)) соответствует истинное значение Y_n+1=X _n+1^T +  _n+1, тогда как пользуясь регрессионной моделью, мы можем получить лишь точечный прогноз _n+1=X _n+1^T.

Пусть =(₀, ₁, … ,_m) – вектор параметров модели, значения которых точно известны, а =(₁, ₂, …, _n) – отклонения в модели регрессии с точно известным значением дисперсии ². В этом случае

M[Y_n+1] = M[X _n+1^T] + M[ _n+1]= M[X _n+1^T] = M[_n+1], мы видим что точечный прогноз _n+1 является несмещенной оценкой Y_n+1. Необходимо оценить ошибку прогноза или отклонение прогнозного значения от истинного:

D[_n+1] = М[(_n+1 -Y_n+1)²]=D[ _n+1]= ².

7.1.1. Понятие об интервальном оценивании и доверительных областях

Вычисляя на основании выборочных данных оценку _n+1=X _n+1^T мы отдаем себе отчет в том, что на самом деле величина _n+1 является лишь приближенным значением неизвестной величины Y_n+1. Возникает вопрос: как сильно может отклоняться это приближенное значение от истинного? В частности, нельзя ли указать такую величину , которая с заранее заданной вероятностью, близкой к единице, гарантировала бы выполнение неравенства | _n+1 - Y_n+1| <? Или, что то же, нельзя ли указать интервал вида (_n+1,1 , _n+1,2), который с заранее заданной вероятностью (близкой к единице) накрывал бы неизвестное нам истинное значение Y_n+1? При этом заранее выбираемая исследователем вероятность обычно называется доверительной вероятностью, а сам интервал (_n+1,1 , _n+1,2) – доверительным интервалом или интервальной оценкой. Ширина доверительного интервала существенно зависит от объема выборки n (уменьшается с ростом n) и от величины доверительной вероятности (увеличивается с приближением доверительной вероятности к единице).

Пусть случайная величина Z подчинена стандартному нормальному закону распределения ZN(0,1), тогда можно записать Prob(|Z|<t_/2)= 1-. Здесь 1- – доверительная вероятность, а t_/2 – критическое значение ( - квантиль), соответствующий . Эта запись эквивалентна интервальной оценке Z (-t_/2 , +t_/2) с доверительной вероятностью 1-.

Если случайная величина X подчинена нормальному закону распределения XN(,), тогда можно записать Prob(|(X- ) / |<t_/2)= 1- (см. 2.6.3), а следовательно, интервальная оценка для примет вид: X(-t_/2 , +t_/2).

7.1.2 Интервальная оценка в прогнозировании

Если ошибка нормально распределена, то интервальная оценка

Y_n+1 (_n+1 -t_; _n+1+ t_), где t_ - двусторонняя  - квантиль стандартного нормального распределения. С вероятностью 1- истинное значение Y_n+1 окажется в данном интервале.

Пусть вектор параметров модели =(₀, ₁, … ,_m) и отклонения =(₁, ₂, …, _n) – неизвестны, а есть только оценки а=(а₀, а₁, … ,а_m) и s_e² – оценки, полученные методом наименьших квадратов (см.4.1.2, ): и .

В этом случае как и в предыдущем точечный прогноз Ŷ_n+1=X _n+1^Tа является несмещенной оценкой истинного значения Y_n+1. Действительно M[a]=, тогда

M[_n+1] = M[X _n+1^Tа] = X _n+1^T M[а] = M[X _n+1^T.] + M[ _n+1]= M[Y_n+1].

Важно, что полученная оценка является эффективной, то есть обладает наименьшей дисперсией.

7.1.3. Дополнительно

Утверждение: Предположим, что - некая несмещенная оценка величины Y_n+1. Тогда необходимо доказать, что .

Доказательство: . Здесь мы использовали тождество в силу несмещенности новой оценки. Рассмотрим дисперсию этой оценки:

Покажем, что . Раскроем скобки и воспользуемся тем, что и _n+1=X _n+1^Tа, а Y_n+1=X _n+1^T +  _n+1

Рассмотрим первое слагаемое

так как Y_n+1=X _n+1^T +  _n+1, то . Окончательно для первого слагаемого получаем:

Рассмотрим второе слагаемое

Третье слагаемое

Четвертое слагаемое

Таким образом, утверждение доказано.

Найдем дисперсию _n+1:

Заменим ² на s_e² , и введем обозначение . Если ошибки (,_n+1) имеют совместное нормальное распределение, то случайная величина (_n+1 - Y_n+1)/ имеет распределение Стьюдента с n-m-1 степенями свободы. Поэтому доверительным интервалом для Y_n+1 с уровнем значимости  будет интервал (_n+1 – t_ , _n+1 + t_), где где t_ - двусторонняя  - квантиль распределения Стьюдента с n-m-1 степенями свободы.

7.2. Прогнозирование при наличии авторегрессии ошибок

Рассмотрим задачу прогнозирования, когда ошибки в исходной модели коррелированы по времени, а именно, образуют авторегрессионный процесс первого порядка. В этом случае связь ошибки в моменты времени i и i-1 выглядит следующим образом:

Здесь _i, i= 1, … , n - последовательность независимых нормально распределенных случайных величин с нулевым средним и постоянной дисперсией _², а ||<1 – коэффициент авторегрессии.

Предположим, что параметры  и  известны.

Истинное значение

Y_n+1=X _n+1^T +  _n+1= X _n+1^T +  _n+  _n+1 = X _n+1^T + (Y_n-X_n^T )+  _n+1

В качестве оценки Y_n+1 возьмем не _n+1=X _n+1^T как раньше, а

_n+1=X _n+1^T+  _n= X _n+1^T + (Y_n-X_n^T ).

Очевидно е = Y_n+1 - _n+1= _n+1, следовательно M[e]=0, D[e]= _²

Сравним дисперсии ошибок для обычной оценки _n+1=X _n+1^T: D[ _n+1]= _ ² , и для оценки _n+1=X _n+1^T+  _n: D[e]= _².

_ ² = D[ _n+1]= D[ _n +  _n+1]=M[( _n +  _n+1)²] =

= M[( _n)²] + M[ _n+1²] + 2M[ _n  _n+1] =²_ ²+_² > _²

Последнее слагаемое равно нулю в силу независимости  _n и  _n+1. Таким образом, удается уменьшить ошибку прогноза по сравнению со случаем некоррелированных ошибок _ ² =_²/( 1- ²).

Реально значения  и  неизвестны, поэтому при прогнозировании величины Y_n+1 их заменяют оценками a и r:

_n+1= = X _n+1^Ta+ r(Y_n-X_n^T a).

7. Вопросы

1. Какие виды прогноза вы знаете?

2. В чем отличие точной и интервальной оценки?

3. Какими характеристиками случайной величины определяется интервальная оценка?

4. В каких моделях подстановка значения х в уравнение регрессии дает смещенную оценку прогнозного значения у?

5. Что такое доверительный интервал?