kurs_lekcii_mo_matematicheskomu_analizu / Векторы. Линейные операции над векторами

ТЕМА 6. ВЕКТОРЫ. ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ.

1.Основные определения

Из курса элементарной физики известно, что некоторые физические величины, как, например, температура, масса, время, плотность, работа, являются скалярными. Некоторые другие величины, такие как сила, скорость, ускорение, напряженность магнитного поля, являются векторными. Скалярная величина может быть охарактеризована одним числом. Векторная величина характеризуется числом и направлением.

Определение 1. Вектором называется направленный отрезок. Если начало вектора находится в точке A , конец в точке B , то вектор обозначается символом AB . Начало вектора называют также точкой его приложения.

Другое обозначение вектора a (a = AB) .

Модулем вектора a называется его длина, т. е. расстояние между его началом и концом, он обозначается через |a| . Модуль вектора скалярная неотрицательная величина.

Нулевым вектором называется вектор, начало и конец которого совпадают. Нулевой вектор обозначается символом 0 . Его модуль равен нулю, а направление не определено.

Единичным вектором называется вектор, длина которого равна единице.

Определение 2. Два вектора a и b называются коллинеарными, если они лежат на одной или на параллельных прямых. Три вектора a, b, c называются компланарными, если они лежат в одной или в параллельных плоскостях.

Определение 3. Коллинеарные векторы, имеющие одинаковые направления и равные длины, называются равными. Векторы, противоположно направленные и имеющие равные длины, называются противоположными.

Вектор, противоположный вектору a, обозначается через −a , а вектору AB через

BA .

*

*

a

c

b

e

d *

Рис. 1

На рис. 1 все векторы попарно коллинеарны; a и c равные векторы, a и b противоположные векторы.

Для каждого вектора точка приложения может быть выбрана произвольно. Соответственно этому в геометрии векторы рассматривают с точностью до их положения (т. е. не различают равных векторов, получающихся друг из друга параллельным переносом). В этом смысле векторы называют свободными.

1

2.Линейные операции над векторами

Линейными операциями над векторами называют сложение, вычитание, умножение вектора на число.

Определение 4. Суммой векторов a и b называют третий вектор c , начало

которого совпадает с началом вектора

, а конец с концом вектора b

при условии,

a

что вектор b отложен из конца вектора

.

a

Вектор

получается по

правилу

треугольника

(рис.

2,

а) или

по правилу

c

параллелограмма (рис. 2, б).

а

1

б

b

>

>

a3 -

a2

*

7

7

AA a4

c

a

a

c

a1

A

A

1

-UA

b

a1 + a2 + a3 + a4

Рис. 2

Рис. 3

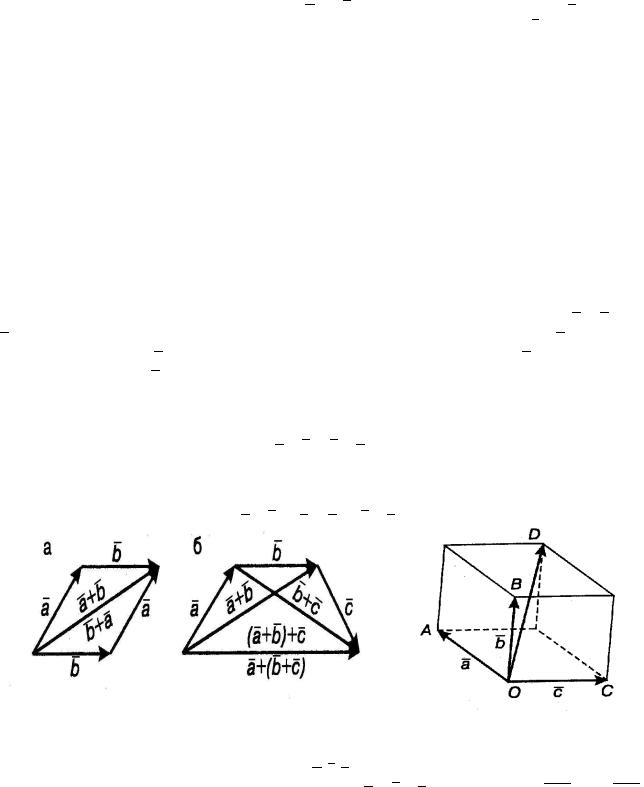
Аналогично определяется сумма трех и более векторов. Суммой n векторов a1, a2, ..., an называется вектор, начало которого совпадает с началом первого вектора a1, конец с концом последнего an при условии, что каждый последующий вектор ak+1 отложен из конца предыдущего ak (k = 1, 2, ..., n − 1) . Такой способ построения суммы называется

правилом замыкания ломаной (рис. 3).

Сумма векторов обладает свойством переместительности (коммутативности, рис. 4, а):

a + b = b + a

и свойством сочетательности (ассоциативности, рис. 4, б):

(a + b) + c = a + (b + c).

Рис. 4

Рис. 5

Сумма трех некомпланарных векторов a, b, c наряду с правилом замыкания ломаной получается и по правилу параллелепипеда: сумма a + b + c равна вектору OD, где OD

2

диагональ параллелепипеда, построенного на векторах OA = a , OB = b , OC = c, отложенных из одной точки (рис. 5).

Из определения суммы следует, что a + 0 = a, a + (−a) = 0.

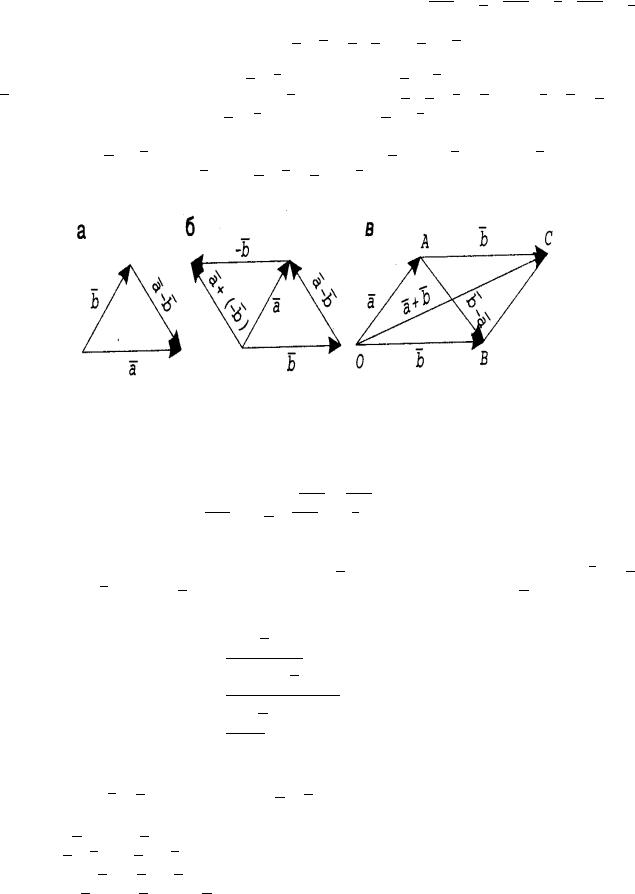
Определение 5. Разностью a − b двух векторов a и b называется такой вектор

d, который при сложении с вектором b дает вектор a : a − b = d, если b + d = a .

Чтобы получить разность a − b двух векторов a и b, необходимо отложить их из одной точки и соединить конец второго вектора с концом первого (рис. 6, а).

Разность a − b равна сумме двух векторов a и (−b) , где (−b) вектор, противоположный вектору b, т. е. a − b = a + (−b) (рис. 6, б).

Рис. 6.

Замечание 1. Векторы диагонали OC и AB параллелограмма OACB (рис. 6, в), построенного на векторах OA = a, OB = b, являются соответственно суммой и разностью этих векторов.

Определение 6. Произведением вектора a на число α называется вектор b = αa, такой, что |b| = |α| · |a|, а направление совпадает с направлением a при α > 0 и противоположно ему при α < 0 (рис. 7).

a-

1, 5a

-

−0, 5a

Рис. 7

Очевидно, b = 0, если α = 0 или a = 0 .

Произведение вектора на число обладает следующими свойствами:

1.α(βa) = (αβ)a;

2.α(a + b) = αa + αb;

3.(α + β)a = αa + βa;

4.(−α)a = α(−a) = −(αa).

3

Из определения 6 следует необходимое и достаточное условие коллинеарности векторов: векторы a и b коллинеарны тогда и только тогда, когда существует число α =6 0 такое, что

			(1)
b = αa.

Пример 1.

В параллелограмме ABCD AB = p , AD = q . Выразить векторы BC, CD, AC, CA, BD, DB через p и q.

				B			C
							>
		p
				-	?

Aq D

Решение. Коллинеарные векторы BC и AD имеют равные длины и одинаково направлены (противоположные стороны параллелограмма равны и параллельны). В соответствии с определением равных векторов получаем BC = AD. Так как AD = q, то

BC = q.

Векторы CD и AB противоположно направлены и имеют равные длины. По определению противоположных векторов получаем

CD = −DC = −AB = −p, т. е. CD = −p.

Вектор AC является суммой векторов AB и BC, но BC = AD, поэтому AC = p + q. Далее, CA = −AC = −(p + q) = −p − q, что можно получить и другим способом:

CA = CD + DA, CD = −p, DA = −AD = −q CA = −p − q.

По определению разности двух векторов получаем BD = AD − AB или BD = q − p,

так как AD = q, AB = p.

Аналогичным образом находим, что DB = p − q.

Пример 2.

Доказать, что при любом расположении точек A , B , C справедлива формула AB +

BC + CA = 0.

Решение. Вектор BC отложен от конца вектора AB, вектор CA от конца вектора BC, тогда конец вектора CA совпадает с началом вектора AB. Следовательно, сумма AB + BC + CA является вектором, начало и конец которого совпадают. Такой вектор по определению есть нуль-вектор, т. е. AB + BC + CA = 0.

4

* a

Пример 3.

Дана пирамида

OABC . Точка M середина стороны

OA , точка

N середина

стороны BC . Положив OA =

OB = b,

OC =

b,

векторы

a,

c, выразить через a,

c

M C и M N .

O

r

J

J

M r

J

C@

J

C @

J

C

@

J

r

Z

@

J

A

C

@ J

C Z

Z

C

@ J

C

b

J

b@

C

b J

@

r

r

bR@^J

r

WC

B

N

C

Решение.

По определению разности двух векторов

получаем

=

−

M C

OC

OM .

условию задачи M середина стороны OA, значит, |

OM

1

OA .

OM

По

1

| =

2 |

|

Векторы

и OA коллинеарны и сонаправлены, следовательно, OM =

2 OA. Но OA =

a, значит,

= 21

;

=

=

− 21

OM

OC

M C

a

c, откуда получаем

c

a.

По определению суммы векторов M N = M C + CN .

Вектор

=

1

(см.

предыдущие рассуждения).

=

−

откуда

CN

CB

CB

OB

OC,

2

1

1

1

получаем CB = b −

2 (b

−

) =

2 b

−

2

c, CN =

c

c,

1

1

1

1

1

1

1

M N =

c

−

a

+

b

−

c

= −

a

+

b

+

c

=

(−

a

+ b +

c

).

2

2

2

2

2

2

2

3.Проекция вектора на ось

Прямая l с выбранным на ней направлением, принимаемым за положительное, называется осью.

Определение 7. Проекцией вектора a на ось l называется число, обозначаемое прla и равное

прl		= |		| · cos ϕ,	(2)
	a		a

где ϕ (0 ≤ ϕ ≤ π) угол между положительным направлением оси l и направлением вектора a.

	!
!!	!
	ϕ			l
!				-

AB

Рис. 8

5

Геометрически проекцию вектора a можно охарактеризовать длиной отрезка AB ,

взятой со знаком

” + ”

, если

ϕ <

π , и со знаком

-

, если

π < ϕ

π (рис. 8). При

π

0 ≤

2

“ “

2

≤

ϕ = 2

отрезок AB превращается в точку и прla = 0.

Проекция вектора на ось обладает следующими свойствами:

1. прl(

+ b) = прl

+ прlb;

a

a

2.

( α число).

прl(αa

) = αпрla

а

b

-

б

в

1, 5a

+ b

a

a

iP

b

3

PP

a + b

:

a

a

пр a

b

b

b

a

l

прl

-

l

пр

l( +

)

прl

-

l

прla

-

l

пр (

a

+ b)

прl

a

пр (1, 5

a

)

l

l

Рис. 9

Рис. 9 иллюстрирует свойства проекций: на (рис. 9а) проекции слагаемых одного знака; на (рис. 9, б) разных знаков.

Пример 4.

Дан вектор a , образующий с осью l угол ϕ1 = 60o , и вектор b , образующий с той же осью угол ϕ2 = 120o . Найти проекцию суммы a + b + c , где c = 3a , на ось l , если

известно, что |a| = 6, |b| = 4 .

Решение. Так как проекция суммы векторов равна сумме их проекций, необходимо найти проекцию каждого слагаемого на ось l. В соответствии с формулой (2) получаем

прla = |a| cos ϕ1 = 6 cos 60o = 6 · 12 = 3;

прlb = |b| cos ϕ2 = 4 cos 120o = 4 · (−12 ) = −2.

По свойствам проекций находим

прlc = прl(3a) = 3 · прla = 3 · 3 = 9,

прl(a + b + c) = прla + прlb + прlc = 3 + (−2) + 9 = 10.

4. Декартовы прямоугольные координаты вектора в пространстве. Действия над векторами, заданными своими координатами

Рассмотрим в пространстве декартову прямоугольную систему координат. Радиусвектором точки M называется вектор r = OM , точка приложения которого совпадает с началом координат, а конец находится в точке M (рис. 10).

6

Рис. 10

Декартовыми прямоугольными координатами X, Y, Z вектора r называются его проекции на координатные оси:

X = прx

Z = прz

r, Y = прy r,

r.

Запись

= (X, Y, Z)

(3)

r

означает, что вектор

имеет координаты

X, Y, Z. Если x, y, z

декартовы

r

прямоугольные координаты точки M, то X = x , Y = y , Z = z, т. е. координаты радиусвектора OM равны координатам точки M.

Введем в рассмотрение единичные взаимно перпендикулярные векторы i , j , k, расположенные на положительных полуосях координатных осей. Они называются ортами. Рассмотрим векторы OA = Xi , OB = Y j , OC = Zk , где A, B, C вершины прямоугольного параллелепипеда, для которого OM является диагональю (A, B, C проекции точки M на координатные оси; OA = X, OB = Y, OC = Z проекции вектора на координатные оси). По определению суммы, OM = OA + OB + OC , поэтому

= Xi + Y j + Zk.

(4)

r

Формула (4) выражает разложение вектора

Векторы

по базисным векторам i, j, k.

r

Xi, Y j, Zk называются составляющими, или компонентами, вектора

.

r

На основании теоремы Пифагора получаем формулу, выражающую длину вектора r

через его координаты:	√X2 + Y 2 + Z2.
|r| =		(5)

В силу определения 7 равные векторы имеют равные проекции, а значит, и равные координаты, поэтому координаты вектора не зависят от точки его приложения.

Координатами любого вектора называются его проекции на координатные оси, т. е.

a = Xi + Y j + Zk = (X, Y, Z).

Рассмотрим два вектора a = X1i + Y1j + Z1k = (X1, Y1, Z1) и b = X2i + Y2j + Z2k = (X2, Y2, Z2), тогда сумма этих векторов

a + b =

7

= X1i + Y1j + Z1k + X2i + Y2j + Z2k = (X1 + X2)i + (Y1 + Y2)j + (Z1 + Z2)k =

= (X1 + X2, Y1 + Y2, Z1 + Z2),

(6)

т. е. координаты суммы векторов равны сумме соответствующих координат.

Аналогично получим

− b = (X1 − X2, Y1 − Y2, Z1 − Z2),

(7)

a

т. е. координаты разности векторов равны разности соответствующих координат.

Найдем координаты вектора c = αa :
c = α(Xi + Y j + Zk) = (αX)i + (αY )j + (αZ)k = (αX, αY, αZ),	(8)

т. е. координаты произведения вектора a на число α равны произведениям соответствующих координат вектора a на α .

Упражнение 1. Доказать, что

необходимым

и

достаточным

условием

коллинеарности двух векторов

=

(X1, Y1, Z1) и b

=

(X2, Y2, Z2)

является

a

пропорциональность их координат:

X1

=

Y1

=

Z1

.

X2

Y2

Z2

Направляющими косинусами вектора называются косинусы углов α, β, γ, образуемых

им с координатными осями. Исходя из определения проекции, имеем

X = |r| cos α,

Y = |r| cos β,

Z = |r| cos γ.

Выражая косинусы и применяя формулу (5), получаем

cos α =

√

X

,

X2 + Y 2 + Z2

cos β =

√

Y

,

(9)

X2 + Y 2 + Z2

cos γ =

√

Z

X2 + Y 2 + Z2

формулы для направляющих косинусов; откуда

cos2 α + cos2 β + cos2 γ = 1.

Координаты единичного вектора

равны его направляющим косинусам, т. е.

=

e

e

(cos α, cos β, cos γ), т. к. |

| = 1. В частности,

e

i = (1, 0, 0),

j = (0, 1, 0),

k = (0, 0, 1).

Если рассмотреть два радиус-вектора

1 = OA1

и

2 = OA2 точек A1(x1, y1, z1) и

r

r

A2(x2, y2, z2), то вектор A1A2 выражается формулой

A1A2 =

2 −

1

(по определению

r

r

разности векторов). Но координаты вектора r1 совпадают с координатами точки A1, а

координаты вектора		2 с координатами A2 , т. е.				1 = (x1, y1, z1),		2 = (x2, y2, z2).
	r				r		r
Откуда, используя формулу (7), получаем
			A1A2 = (x2 − x1, y2 − y1, z2 − z1),				(10)

8

т. е. координаты вектора равны разности соответствующих координат его конца и начала.

Формула (5) в этом случае принимает вид

p

|A1A2| = (x2 − x1)2 + (y2 − y1)2 + (z2 − z1)2 (11)

и выражает расстояние между точками A1 и A2.

Пример 5.

Даны векторы: a1 = (2, 4, −6), a2 = (−1, −2, 3), a3 = (4, 8, −12), a4 = (6, 0, 0), a5 = (0, −5, 0), a6 = (0, 0, 2), a7 = (0, 1, 3), a8 = (2, 0, −1), a9 = (3, −4, 0). Какие из этих векторов коллинеарны, параллельны координатным осям, параллельны координатным плоскостям?

Решение. Так как координаты векторов a1 и a2 пропорциональны, т. е.

2

=

4

=

−6

=

2,

1

−

2

3

−

−

то векторы

1 и

2 коллинеарны. Поскольку

2

= −2

1 , векторы

1 и

2

a

a

a

a

a

a

противоположно направлены. Векторы

1

и

3 также коллинеарны, ибо

a

a

2

=

4

=

−6

=

1

.

4

8

−12

2

Векторы

1

и

3 одного направления, так как

1

= 2

3 . В силу коллинеарности

1 и

a

a

a

a

a

2,

1 и

3

можно сделать вывод о коллинеарности векторов

2 и

3

(

3 = −4

2 ).

a

a

a

a

a

a

a

Сравнивая координаты векторов

6 с

координатами

векторов

4,

5,

i, j, k,

a

a

a

заключаем, что вектор

4 параллелен оси Ox, вектор

5 оси Oy, вектор

6

оси

a

a

a

Oz (

4 и i

коллинеарны, так как

4 = 6i,

5 и j

коллинеарны, ибо

5 = −5j,

6 и k

a

a

a

a

a

также коллинеарны, ибо

6 = 2k ).

a

Поскольку у вектора

7 координата

x = 0 , т. е. проекция на ось

Ox равна нулю,

a

то вектор

7 перпендикулярен оси

Ox

и, следовательно, параллелен плоскости Oyz.

a

Аналогичным образом заключаем, что вектор a8 параллелен плоскости Oxz, а вектор a9 плоскости Oxy.

Замечание 2. Если одна из координат вектора равна нулю, то вектор перпендикулярен соответствующей координатной оси.

Замечание 3. Если вектор имеет только одну отличную oт нуля координату, то он параллелен соответствующей координатной оси.

Пример 6.

Определить, при каких значениях α и β векторы a = 2i + αj + k и b = 3i − 6j + βk коллинеарны.

Решение. Координаты векторов a = (2, α, 1) и b = (3, −6, β) должны быть пропорциональны:

32 = −α6 = β1 .

Отсюда находим, что α = −4 , β = 32 . При этих значениях α и β векторы a и b коллинеарны.

9

Пример 7.

На оси ординат найти точку, равноудаленную от точек A(1, −3, 7) и B(5, 7, −5). Решение. Так как искомая точка M лежит на оси ординат, она имеет координаты

M (0, y, 0).

По условию задачи |M A| = |M B|. Вычислим |M A| и |M B|, используя формулу (11):

p p

|M A| = (1 − 0)2 + (−3 − y)2 + (7 − 0)2 = 50 + (3 + y)2,

p p

|M B| = (5 − 0)2 + (7 − y)2 + (−5 − 0)2 = 50 + (7 − y)2.

Из условия |M A| = |M B| получаем

p p

50 + (3 + y)2 = 50 + (7 − y)2.

Возводим обе части равенства в квадрат:

50 + (3 + y)2 = 50 + (7 − y)2,

(3 + y)2 = (7 − y)2,

y2 + 6y + 9 = y2 − 14y + 49,

			20y = 40,
				y = 2.
Итак, искомая точка M (0, 2, 0).
Пример 8.
Даны вершины A(2, 2, 2),			B(6, 5, 0),		C(0, 3, 8)		параллелограмма ABCD. Найти
вершину D.
	B				-	C
			-
A				D
Решение. Обозначим координаты					точки		D(x, y, z). Так как ABCD

параллелограмм, его противоположные стороны параллельны и равны, т. е. BC = AD. Найдем координаты векторов BC и AD :

BC = (0 − 6, 3 − 5, 8 − 0) = (−6, −2, 8), AD = (x − 2, y − 2, z − 2).

Если векторы равны, то равны и их соответствующие координаты, т. е. −6 = x − 2,

−2 = y − 2, 8 = z − 2.

Откуда x = −4, y = 0, z = 10. Следовательно, D(−4, 0, 10).

5.Деление отрезка в данном отношении

Пусть l некоторая прямая и AB отрезок на l .

10