kurs_lekcii_mo_matematicheskomu_analizu / Упрощение уравнения кривых второго порядка

ТЕМА 14. УПРОЩЕНИЕ КРИВЫЕ ВТОРОГО ПОРЯДКА.

Общее уравнение кривой второго порядка имеет вид (1)

Ax2 + 2Bxy + Cy2 + 2Dx + 2Ey + F = 0.

Если это уравнение не содержит члена с произведением координат, т. е. 2B = 0, то дополняя члены, содержащие x, y, до полных квадратов, при помощи параллельного переноса можно привести уравнение к каноническому виду.

Если же 2B 6= 0, то с помощью поворота осей можно избавиться от члена с произведением координат. В результате получим канонические уравнения.

1.Параллельный перенос системы координат

Рассмотрим две системы координат Oxy и O1XY с одинаковым направлением осей координат, но разными началами координат.

Y

6

y

6

M (x, y)

*

(X, Y )

-

Qk

O1

QQ

X

Q

-

O

x

Пусть на плоскости взята точка

M и пусть

(x, y) – ее координаты в системе Oxy и

(X, Y ) – в системе O1XY, а координаты точки O1 в системе Oxy O1(a, b).

OO1 + O1M = OM ,

или, в координатах,

X + a = x и Y + b = y.

Имеем формулы для перехода от старых координат точки M к ее новым координатам:

x = X + a, y = Y + b.

Формулы, выражающие новые координаты через старые, запишутся

X = x − a, Y = y − b.

Пример 1.

Построить линию, определяемую уравнением

9x2 − 16y2 − 36x − 32y − 124 = 0

(14)

(15)

1

X2

16

9(x − 2)2 − 16(y + 1)2 − 144 = 0,

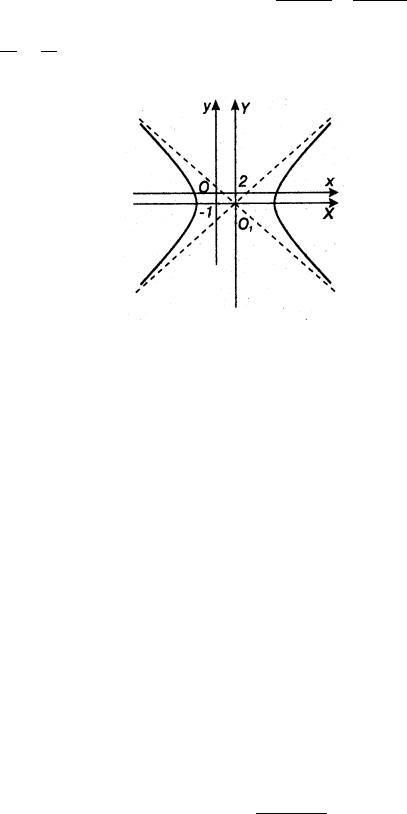
Решение. Преобразуем исходное уравнение, выделив полные квадраты:

9(x2 − 4x + 4) − 16(y2 + 2y + 1) − 36 + 16 − 124 = 0,

(x − 2)2 − (y + 1)2 = 1. 16 9

Перейдем к новым координатам по формулам (15): X = x − 2, Y = y + 1, получим уравнение − Y92 = 1, определяющее гиперболу с полуосями a = 4, b = 3. Центр гиперболы находится в точке, для которой X = 0, Y = 0.

Так как X = x − 2, Y = y + 1, то x − 2 = 0, y + 1 = 0, откуда x = 2, y = −1.

Получена точка O1(2, −1), в которой находится начало новой системы координат.

2.График квадратного трехчлена

Пусть дано уравнение

y = Ax2 + Bx + C.

Чтобы получить простейшее уравнение данной кривой, подставим вместо старых координат x и y их выражения через новые координаты X, Y из формул параллельного переноса (14) в уравнение y = Ax2 + Bx + C :

Y + b = A(X + a)2 + B(X + a) + C.

После упрощений получим

Y = AX2 + (2Aa + B)X + Aa2 + Ba + C − b.

Выберем координаты нового начала a и b так, чтобы в правой части последнего уравнения коэффициент при X и свободный член обратились в нуль:

2Aa + B = 0,

Aa2 + Ba + C − b = 0.

Решая эту систему уравнений относительно неизвестных a, b, получим

a =	−	B		, b =	4AC − B2	.
		2A
					4A

2

При таком выборе начала координат O1 новой системы координат уравнение y = Ax2 + Bx + C примет вид Y = AX2, т. е. будет простейшим уравнением параболы, для которой ось O1Y является осью симметрии.

Пример 2.

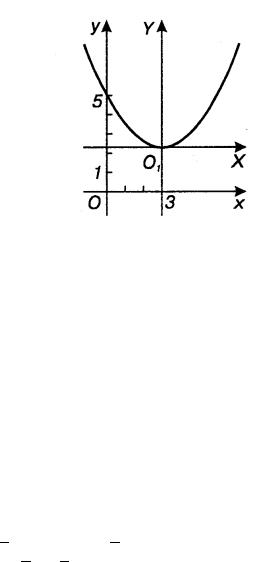
Построить линию, определяемую уравнением 3y = x2 − 6x + 15. Решение. Преобразуя это уравнение, получаем

y = 13 ((x2 − 6x + 9) + 6), y = 13 (x − 3)2 + 2, y − 2 = 13 (x − 3)2.

Перейдем к новым координатам по формулам (15): X = x − 3, Y = y − 2. В новых координатах уравнение примет вид Y = 13 X2 , или X2 = 3Y ; оно определяет параболу.

Строим системы координат Oxy и O1XY, последнюю с началом в точке O1(3, 2), и саму параболу – в новой системе координат по ее каноническому уравнению.

3. Поворот системы координат

Рассмотрим выражение
Ax2 + 2Bxy + Cy2,	(16)

которое представляет собой многочлен второй степени относительно переменных x и y

и называется квадратичной формой.

Тогда матрица	C	(17)
B
A	B

называется матрицей квадратичной формы.

Рассмотрим линейное преобразование, заданное матрицей (17). Пусть λ1 и λ2 его собственные числа, а a1 = (α1, β1) и a2 = (α2, β2) собственные векторы.

Нормируем векторы a1 и a2 :

l1

= |a1|

=

|a1|,

|a1

|

, l2 = |a2|

=

|a2|,

|a2

|

a1

α1

β1

a2

α2

β2

и составим матрицу S :

a1

a2

!

α1

α2

|

1

|

|

2

|

S =

a

a

.

(18)

β1

β2

|

|

|

|

3

Линейное ортогональное преобразование

x

y

=

α1

|a1|

β1

|a1|

α2

|a2|

β2

|a2|

!

·x1 y1

осуществляет поворот системы координат. Ортами, задающими новую систему Ox1y1 , являются векторы l1 , l2, а выражение (16) в системе Ox1y1 примет вид λ1x21 + λ2x22.

Замечание 4. Определитель матрицы S равен ±1 : |S| = ±1. В том случае, когда |S| = 1, взаимная ориентация новых координатных осей сохраняется; если |S| = −1 , их ориентация меняется на противоположную.

Пример 3.

Привести к каноническому виду уравнение линии второго порядка и построить кривую

5x2 − 6xy + 5y2 − 24x + 8y + 24 = 0.

Решение. Группа старших членов данного уравнения образует квадратичную форму

5x2 − 6xy + 5y2.

5

−3 .

Ее матрица A =

−3

5

Характеристическое уравнение в данном случае принимает вид

5 −3λ

5−3λ

= (5 − λ)2 − (−3)2 = 0,

−

−

2

,

.

или λ

− 10λ + 16 = 0.

Откуда λ1

= 2

λ2

= 8

Получим систему для определения собственных векторов. Пусть

= (α, β), тогда

a

Aa

= λa или

5

−3

α

= λ

α

5α − 3β = λα,

−3 5

β

β

−3α + 5β = λβ.

Следовательно,

(5 − λ)α − 3β = 0,

−3α + (5 − λ)β = 0.

При λ1 = 2 получим систему

3α − 3β = 0,

Откуда β = α. Положив α = c, где

−3α + 3β = 0.

c – произвольная постоянная, найдем первый собственный вектор

a

1 = (c, c).

При λ2 = 8 получим систему

−3α − 3β = 0,

Откуда α =

β. Положив β = c,

−3α − 3β = 0.

−

где c

– произвольная постоянная, найдем второй собственный вектор

a

2 = (−c, c).

Вычислим длины векторов

1

и

2 :

a

a

1| = √

= c√

2| = p

= c√

.

|

c2 + c2

2

, |

(−c)2 + c2

2

a

a

Отсюда

c

c

1

1

c

c

1

1

l1 = (

√

,

√

) = ( √

, √

),

l2 = (−

√

,

√

) = (−√

, √

).

c 2 c 2

2

2

c 2 c 2

2 2

4

Применяя формулу (18), составляем матрицу S :

S = √		√		! .
1		1
1		−1
	√2	√2

22

Связь между старыми и новыми координатами осуществляется по формуле:

y

=

√2

√2

!

· y1

.

1

1

x

1

−1

x1

√2

√2

1

1

Откуда:

x =

(x1

− y1),

y =

(x1

+ y1). Подставим полученные выражения в

√

√

2

2

уравнение кривой:

1

2

1

1

2

5 ·

(x1

− y1)

− 6 ·

(x1 − y1)(x1 + y1) + 5 ·

(x1

+ y1)

−

2

2

2

1

1

−24 · √

(x1 − y1) + 5 · √

(x1

+ y1) + 24 = 0.

2

2

Раскрыв скобки и приведя подобные, получим

√√

2x21 + 8y12 − 8 2x1 + 16 2y1 + 24 = 0.

Последнее уравнение не содержит произведения координат, значит, при помощи параллельного переноса его можно привести к каноническому виду. Для этого выделим полные квадраты:

2(x12 − 4√

x1 + 8) + 8(y12 + 2√

y1 + 2) − 16 − 16 + 24 = 0,

2

2

2√

2)2 + 8(y1 + √

или

(x1 − 2√

+

(y1 + √

2)2

2)2

2(x1

−

2)2

−

8 = 0

= 1.

4

√

1

√

Перейдем к новым координатам по формулам (14): X = x1 − 2 2, Y

= y1 + 2. В

системе координат O1XY получим уравнение

X2

Y 2

+

= 1,

4

1

определяющее эллипс с полуосями a = 2, b = 1. Центр эллипса находится в точке, для

которой

X

= 0, Y = 0. Так как

X

= x1 − 2√

,1

Y = y1 +

√

, 1то x1 − 2√

= 0,

2

2

2

√

√

√

y1 +

2 = 0, откуда x1 = 2

2, y1 = − 2. Но x =

√

(x1 − y1),

y =

√

(x1 + y1), значит,

2

2

1

√

√

1

√

√

– координаты точки O1 в системе

x =

√

(2

2 − (− 2)) = 3,

y =

√

(2

2 − 2) = 1

2

2

Oxy.

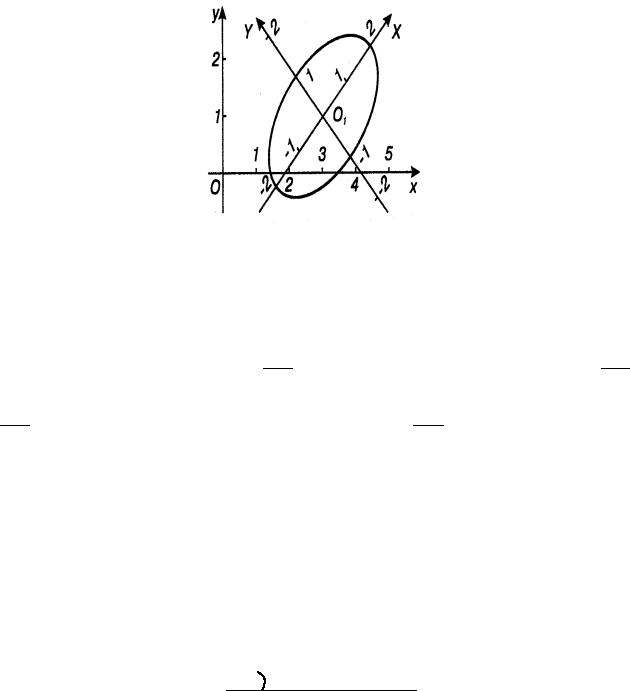
Чтобы построить искомую кривую, в системе координат Oxy наносим точку O1(3, 1),

из точки	O1 строим векторы		1			1				и		1			1				которые задают оси O1X
		l1 = (		√		,	√		)		l2 = (−		√		,	√		),
					2			2						2			2

и O1Y соответственно. Затем на оси O1X откладываем полуоси 2 и −2 , а на оси O1Y

– полуоси 1 и −1 и рисуем эллипс.

5

4.Полярная система координат

Выберем на плоскости некоторую фиксированную точку O – начало координатной системы, или полюс. Фиксированный луч с выбранным на нем единичным вектором и с началом в полюсе назовем полярной осью.

Положение любой точки M на плоскости можно определить упорядоченной парой

чисел: длиной r радиуса-вектора OM и углом ϕ между полярной осью и OM . Угол считается положительным, если направление вращения от оси к радиусу-вектору берется против часовой стрелки. Запись M (r, ϕ) показывает, что длина радиуса-вектора

|OM | = r, а угол между полярной осью и радиусом OM равен ϕ. Числа r и ϕ называются полярными координатами точки M. Длина радиус-вектора r для разных точек плоскости может меняться от 0 до +∞, полярный угол ϕ определяется с точностью до слагаемого, кратного 2π .

Установим связь между декартовыми и полярными координатами точки M.

Поместим начало декартовой системы координат в полюсе полярной системы и направим

ось абсцисс по полярной оси.y

6

r

r M

y

ϕ

-

x

|

x

}

Тогда

{z

x = r cos ϕ,

y = r sin ϕ ϕ [0, 2π)

(19)

и

x

y

y

r = px2 + y2,

cos ϕ =

,

sin ϕ =

,

x2 + y2

x2 + y2

tg ϕ = x .

p

p

Для построения линии, заданной уравнением в полярной системе координат, используют метод построения "по точкам": вычисляют координаты ряда точек линии и соединяют эти точки плавной кривой.

Пример 4.

6

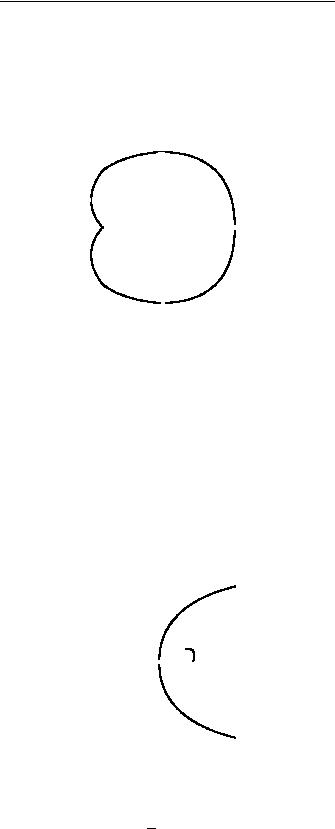
Построить линию r = 2(1 + cos ϕ). Решение. Составляем таблицу.

ϕ

0

π/6

π/3

π/2

2π/3

5π/6

π

4

√

√

r

2 + 3

3

2

1

2 − 3

0

Так как cos ϕ = cos(2π − ϕ), то вычислять значения при

π < ϕ < 2π не нужно.

Кривая симметрична относительно полярной оси. Нанося соответственные точки на чертеж и соединяя их плавной линией, получаем вид рассматриваемой линии. Эта линия называется кардиоидой.

r

r

r

""""

r

""

"

"

-

5.Полярное уравнение эллипса, гиперболы и параболы

Пусть дана линия L – эллипс, гипербола (будем рассматривать какую-нибудь одну ее ветвь) или парабола. Пусть F – фокус линии, g – соответствующая этому фокусу директриса.

Введем полярную систему координат так, чтобы полюс совместился с фокусом, а полярная ось совпала с фокальной осью линии L в направлении от директрисы g к фокусу.

g							L
	d				M
			P			r
S
				r
				ϕ			-
D			F		N

Рассмотрим на линии L произвольную точку M. Ее полярные координаты обозначим r и ϕ : M (r, ϕ). Для эллипса, гиперболы и параболы справедливо соотношение

dr = ε,

7

где ε – эксцентриситет линии, r – расстояние от точки до фокуса, d – расстояние от точки до директрисы.

d = |DN | = |DF | + |F N | = |DF | + r cos ϕ.

(20)

Пусть P – точка на линии L расположена так,

что F P r DN

и |F P | = p, где p

– фокальный параметр линии L. Вследствие соотношения

d = ε имеем для точки P :

|F P |

= ε, откуда

|SP |

|F P |

p

|

SP

|

=

=

,

ε

ε

но |SP | = |DF |, следовательно, |DF | = pε . Подставив |DF |

в (20), получим

d =

p

+ r cos ϕ

ε

и, наконец, подставив d в соотношение

r

= ε,

d

будем иметь

r

p/ε + r cos ϕ = ε

или	p
r =		.	(21)
	1 − ε cos ϕ

Это и будет полярное уравнение эллипса, гиперболы и параболы.

8