kurs_lekcii_mo_matematicheskomu_analizu / Функциональная зависимость

ЛЕКЦИЯ 1. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ.

1.Понятие функции

Понятие функции, наряду с понятием числа и переменной величины, является одним из главнейших понятий современной математики. В естествознании и технике мы часто встречаемся с зависимостями одних величин от других с так называемыми функциональными зависимостями.

Функциональная зависимость одной величины (y) от другой (x) означает, что каждому значению x соответствует единственное значение y . Величина x при этом называется независимой переменной, а y зависимой переменной, или функцией этой переменной. Также говорят, что x аргумент функции y .

Термин ¾функция¿ впервые был введен в 1692 г. Готфридом Вильгельмом Лейбницем.

Примеры:

1. Площадь S квадрата является функцией длины a его стороны: S = a2 . 2. Объем V шара можно выразить через радиус R шара:

V= 43 πR3.

3.Объем конуса V с данной высотой h зависит от радиуса r его основания:

V= 13 πr2h.

4.Пусть путь z , пройденный свободно падающим телом, зависит от времени t ,

протекшего с момента, когда началось падение. Эта зависимость выражается формулой z = gt22 ( g ускорение свободного падения).

Определение 1. Если каждому значению, которое может принять переменная x , по некоторому правилу или закону ставится в соответствие одно определенное значение переменной y , то говорят, что y есть однозначная функция от x , и обозначают y = f (x) .

Множество всех значений аргумента x , для которых функция y = f (x) определена, называется областью определения этой функции (О.О.Ф.).

Множество всех значений, принимаемых переменной y , называют областью значений функции (О.З.Ф.) функции y = f (x) .

Функция называется четной, если для любого x из области определения выполняется равенство f (−x) = f (x).

Функция называется нечетной, если для любого x из области определения выполняется равенство f (−x) = −f (x).

Функция называется периодической с периодом T > 0, если при любом x из области

определения выполняется равенство f (x − T ) = f (x) = f (x + T ).
Пример 1. Найти О.О.Ф. y = √		.
	4 − x2		2	, т. е. |x| ≤ 2	, следовательно,
Решение. Функция имеет смысл, когда 4 − x ≥ 0
О.О.Ф. есть отрезок [−2, 2] .			x−1
Пример 2. Найти О.О.Ф., О.З.Ф. y = arcsin
			4

1

Решение. Область определения арксинуса – множество точек из отрезка [−1, 1]. Следовательно, задача сводится к решению неравенства

1

x − 1

≤

1.

− ≤

4

Отсюда

−4 ≤ x − 1 ≤ 4,

−3 ≤ x ≤ 5.

Итак, О.О.Ф. есть отрезок [−3, 5].

О.З.Ф. есть отрезок [−π/2, π/2].

x3

x5

Пример 3. Доказать, что функция f (x) = x −

−

является нечетной.

3

5

Решение.

f ( x) = ( x)

−

(−x)3

+

(−x)5

= x +

x3

−

x5

=

3

5

5

−

−

−

3

= − x −

x3

+

x5

= −f (x).

3

5

Итак, f (−x) = −f (x), т. е. функция нечетная.

Пример

4.

Показать, что

функция f (x)

=

tg x sin 3x + ctg 2x является

периодической, и найти ее период.

Решение. Функция tg x имеет период π,

2π

sin 3x = sin(3x + 2π) = sin 3

x +

,

3

т. е. функция sin 3x

имеет период

2π

,

3

ctg 2x = ctg(2x + π) = ctg h2

x +

π

i ,

2

т. е. функция

ctg 2x имеет период

π2 , тогда функция

f (x) имеет период, равный

наименьшему кратному чисел π,

2π

,

π2 , т. е. 2π. В самом деле,

3

f (x + 2π) = tg(x + 2π) sin(3x + 2π) + ctg(2x + 2π) =

= tg x sin 3x + ctg 2x = f (x).

Итак, f (x + 2π) = f (x), т. е. функция периодическая с периодом 2π.

2.Способы задания функции

Аналитический способ это задание функции с помощью формул или уравнений.

Например: y = sin x, y = x2, y2 + x2 = 1 и т. д.

Если уравнение, при помощи которого задается функция, не разрешено относительно y , то функция называется неявной. Когда такое решение возможно, неявная функция может быть приведена к явной форме, т. е. к виду y = f (x) .

2

Например, уравнение 2x + 3y − 5 = 0 можно рассматривать как функцию, заданную неявно. Решив его относительно y , мы получим ту же функцию, но уже в явном виде:

y = 5 − 2x .

3

Отметим, что при аналитическом способе задания функции встречаются случаи, когда функция задана не одной, а несколькими формулами, например:

	x,		x > 0.
y =	x2	,	x ≤ 0,
	−

Табличный способ это способ задания функции при помощи таблицы. Примерами такого задания являются таблицы тригонометрических функций, логарифмов и т. д. Табличный способ задания функции широко используется в различного рода экспериментах и наблюдениях. Таблицы просты в обращении, но недостатком этого способа является то, что функция задается не для всех значений аргумента.

Графический способ. Графиком функции y = f (x) называется множество точек (x, y) плоскости XOY , координаты которых связаны соотношением y = f (x) .

Преимуществом графического способа задания функции является его наглядность. Графический способ задания функции используется при работе различных самопишущих приборов. В медицине, например, работа сердца анализируется с помощью кардиографа.

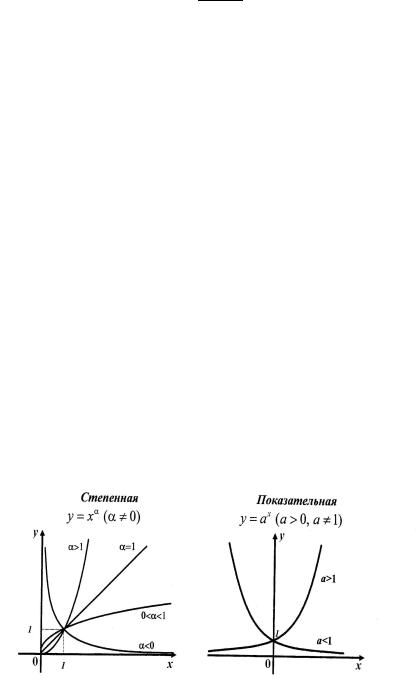
Функции cтепенная, показательная, логарифмическая, тригонометрическая, обратные тригонометрические, постоянная (константа) называются основными элементарными функциями.

Графики основных элементарных функций

Рис. 1

3

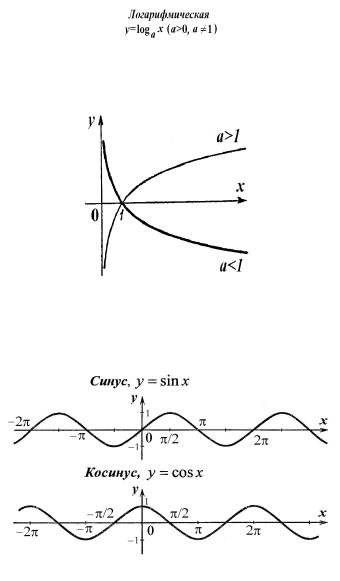
Рис. 2

Рис. 3

4

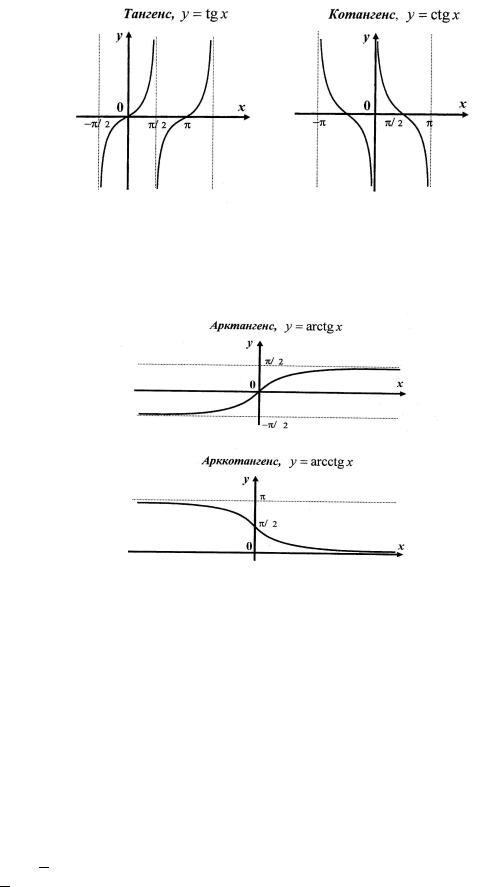
Рис. 4

Рис. 5

3.Многозначные функции

Иногда приходится рассматривать ситуацию, когда каждому значению независимой переменной x ставится в соответствие несколько значений y. В этом случае говорят, что

функция y = f (x) многозначная.

многозначных функций: y = ±√

В алгебре и геометрии много примеров

y =

x,

Arcsinx, y = Arctgx ( Arcsinx , Arctgx

пишем

вместо arcsin x,

arctg x в случае

многозначной функции).

Так, например, функция √

определена для

2 x ≥ 0 и рассматривалась

как

x

однозначная. Однако, решая уравнение параболы y

= x относительно y, получаем,

что y = ±√

x. Выражение ±√

можно рассматривать, как функцию

√

x

x, двузначную

для √x > 0 : каждому положительному соответствуют два действительных числа,

5

отличающихся между собой знаками, квадраты которых равны x . Что же касается функции Arcsinx , то она приводит в соответствие каждому значению x из отрезка [−1, 1] бесконечное множество значений y , которые могут быть записаны по формуле

y = (−1)k arcsin x + πk, (k = 0, 2, . . .).

Если приходится рассматривать функцию как многозначную, то это необходимо оговаривать особо.

4.Обратная функция

Если уравнение y = f (x) может быть однозначно разрешено относительно x , то говорят, что функция x = g(y) обратная по отношению к y = f (x) . Обозначается x = f −1(y) . Причем y ≡ f (f −1(y)).

Иногда придерживаются стандартных обозначений: под x понимают независимую переменную, а под y функцию, т. е. зависимую переменную. В таком случае обратную функцию следует писать в виде y = g(x) .

Например, можно говорить, что функции y = 2x и y = log2 x являются взаимно обратными. Чтобы из графика данной функции y = f (x) получить график обратной ей функции y = g(x) , достаточно первый график симметрично отобразить относительно биссектрисы 1-го и 3-го координатных углов.

Пример 5. Дана функция y = 1 − 2−x . Найти обратную функцию.

Решение.

2−x = 1 − y, x = − lg(1 − y) . lg 2

Область определения функции (О.О.Ф.) −∞ < y < 1 .

5.Сложная функция

Пусть переменная y зависит от переменной u , которая в свою очередь зависит от переменной x : y = f (u), u = ϕ(x) . Тогда при изменении x будет меняться u , а потому будет меняться и y . Значит, y является функцией x : y = f (ϕ(x)). Эта функция называется сложной функцией (или функцией от функции), переменная u – промежуточной. Указанную сложную функцию называют также суперпозицией функций f и ϕ .

Пример 6. Дана функция f (x) = arccos(lg(x)) . Найти а) f ( 101 ); б) f (1); в) f (10).

Решение.

а) f ( 101 ) = arccos(lg( 101 )) = arccos(−1) = π.

б), в) вычислить самостоятельно.

Всякая функция, которая получается из основных элементарных функций путем конечного числа суперпозиций и четырех арифметических действий, называется элементарной функцией. Например, многочлен степени n элементарная функция.

6

6.Параметрический способ задания функции

Говорят, что функция задана параметрически, если зависимость y от x задана с помощью параметра t : где t пробегает некоторые числовые значения.

x

= cos t,

t [0, 2π].

Пример 7.

Задана функция y

= sin t,

При каждом значении

t получаем пару чисел, определяющих точки на плоскости.

Например, возьмем следующие значения параметров:

t

0

π/6

π/3

π/2

2π/3

5π/6

π

7π/6

4π/3

x

1

√

0.5

0

-0.5

√

-1

√

-0.5

3/2

− 3/2

− 3/2

y

0

0.5

√

1

√

0.5

0

-0.5

√

3/2

3/2

− 3/2

Если построить эти точки на плоскости XOY, можно увидеть, что при непрерывном изменении t [0, 2π] мы получим окружность радиуса единица с центром в начале координат. Или можно поступить по другому, исключить параметр t, тогда x2 + y2 = cos2 t + sin2 t = 1.

7.Построение графиков функций

Рассмотрим простейшие преобразования графиков функции.

1.График функции y = f (x + a) получается из графика функции y = f (x) параллельным сдвигом его вдоль оси Ox на |a| единиц масштаба в направлении, противоположном знаку a.

2.График функции y = f (kx) (k > 0) получается из графика функции y = f (x)

”сжатием” его к оси Oy в k раз при k > 1 и ”растяжением” от оси Oy в 1/k раз при

k< 1.

3.График функции y = kf (x) (k > 0) получается из графика функции y = f (x)

”растяжением” его от оси Ox в k раз при k > 1 и ”сжатием” к оси Ox в 1/k раз при

k< 1.

4.График функции y = f (x) + b получается из графика функции y = f (x) параллельным сдвигом его вдоль оси Oy на |b| единиц масштаба в направлении, совпадающим со знаком b.

5.График функции y = −f (x) симметричен графику функции y = f (x) относительно оси Ox.

Рассмотрим построение графика функции y = kf (mx + b) + a путем преобразования графика функции y = f (x). Предварительно выполним тождественное преобразование

y = kf (mx + b) + a = kf	m	x + m		+ a.
			b

Теперь последовательно применяя преобразования 1 – 5, строим искомый график функции.

Пример 8. Построить график функции y = 3 sin(2x + 4) преобразованием графика функции y = sin x.

Решение. Выполним тождественное преобразование

y = 3 sin(2x + 4) = 3 sin 2(x + 2).

7

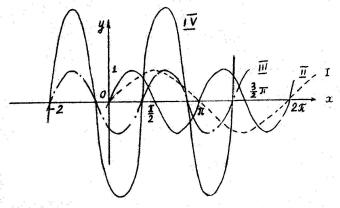
Будем строить график функции в следующем порядке. 1. Строим график функции y = sin x на сегменте [0, 2π].

2.График функции y = 2 sin x получится сжатием графика функции y = sin x в два раза вдоль оси абцисс.

3.Для построения графика функции y = sin 2(x + 2) надо график функции y = sin 2x перенести влево вдоль оси абцисс на две единицы.

4.График функции y = 3 sin 2(x + 2) получим из графика функции y = sin 2(x + 2) растяжением его вдоль оси ординат в три раза.

I. y = sin x. II. y = sin 2x.

III. y = sin 2(x + 2). IV. y = 3 sin 2(x + 2).

8