kurs_lekcii_mo_matematicheskomu_analizu / Асимптоты графика функций

ЛЕКЦИЯ 13. АСИМПТОТЫ ГРАФИКА ФУНКЦИИ. ОБЩАЯ СХЕМА ИССЛЕДОВАНИЯ ГРАФИКА ФУНКЦИИ.

1.Асимптоты графика функции

Определение 1. Прямая x = a называется вертикальной асимптотой графика

функции y = f (x), если хотя бы одно из предельных значений lim f (x) или	lim f (x)
x→a+0	x→a−0
равно +∞ или −∞.

Замечание 1. Непрерывные функции вертикальных асимптот не имеют.

1

Пример 1. Найти вертикальные асимптоты функции y = x − a .

Решение. Прямая x = a вертикальная асимптота (рис. 10), так как

lim			1		= +∞,	lim	1		= −∞.
			− a
x→a+0 x						x→a−0 x − a
	y
				6
							-
						a		x

Рис. 10

Пример 2. Найти вертикальные асимптоты функции y = ln x.

Решение. Прямая x = 0 вертикальная асимптота, так как lim ln x = −∞ (рис.

						x→0+0
11).
y
					y = ln x
		6
					-	x
				1

Рис. 11

Определение 2. Прямая y = kx + b называется наклонной асимптотой графика функции y = f (x) при x → +∞ (−∞), если

1

f (x) = kx + b + α(x),

(1)

где lim α(x) = 0 (рис. 12).

x→+∞ (x→−∞)

y

6

y = kx + b

y = f (x)

-

x

Рис. 12

В разделе "Аналитическая геометрия"мы уже встречались с понятием наклонной асимптоты при построении гиперболы.

Утверждение 1. Прямая y = kx + b является наклонной асимптотой графика функции y = f (x) при x → +∞ (−∞) тогда и только тогда, когда существуют

	k = lim	f (x)	,	b = lim (f (x) − kx),
		x
	x→+∞			x→+∞
	(x→−∞)			(x→−∞)

причем при x → +∞ ( x → −∞ ) наклонная асимптота называется правой (левой).

Доказательство. Предположим, что кривая y = f (x) имеет наклонную асимптоту y = kx + b при x → +∞, т. е. имеет место равенство (1). Тогда

k = f (xx) − xb − α(xx) .

Переходя к пределу при x → +∞, получаем

k = lim f (x) .

x→+∞ x

Далее из равенства (1) b = f (x) −kx −α(x). Переходя к пределу при x → +∞, получаем

b = lim (f (x) − kx).

x→+∞

Докажем обратное утверждение. Пусть пределы, указанные в теореме, существуют и конечны. Следовательно,

f (x) − kx = b + α(x),

где α(x) → 0 при x → +∞ (x → −∞). Отсюда и получаем представление (1). Теорема доказана.

2

Пример 5.

Решение. 1)

Замечание 2. При k = 0 прямая y = b называется горизонтальной асимптотой, причем при x → +∞ ( x → −∞ ) – правой (левой).

Пример 3. Найти наклонные асимптоты функции y = ln x.

Решение. Так как y = ln x определена при x > 0, ищем наклонную асимптоту при x → +∞.

		ln x			1
	k = lim		=	lim	x	= 0,
		x			1
	x→+∞			x→+∞
	b = lim (ln x − 0 · x) = lim				ln x = +∞.
	x→+∞			x→+∞

Поэтому y = ln x не имеет наклонных асимптот.

Пример 4. Найти наклонные асимптоты функции y = x3 + 2 .

2x2 + 1

Решение.

f (x)

x3 + 2

1

k = lim

= lim

=

,

x

x→∞

x→∞ x(2x2 + 1)

2

x→∞

x→∞

x3 + 2

1

2 − x

= 0

2x2 + 1

2

= x→∞ 2(2x2 + 1)

b = lim (f (x) − kx) = lim

−

x

lim

.

y = 12 x наклонная асимптота и при x → +∞ , и при x → −∞. Найти асимптоты функции y = x + arctg x.

x→+∞

x

= x→+∞

x

k1 = lim

x + 2 arctg x

lim

1 +

2 arctg x

= 1;

b1 = lim (x + 2 arctg x − x) = 2 lim

arctg x = 2 ·

π

= π;

2

x→+∞

x→+∞

y = x + π правая наклонная асимптота.

2)

x + 2 arctg x

k2 = lim

= 1;

x

x→−∞

b2

lim (x + 2 arctg x − x) = 2 lim

arctg x = 2

−

π

−π

2 =

;

= x→−∞

x→−∞

y = x − π левая наклонная асимптота.

Пример 6.

Найти асимптоты функции y = x2e−x .

Решение. Функция непрерывна, следовательно, вертикальных асимптот нет.

Определим, существуют ли наклонные асимптоты.

k1 =

lim

x2e−x

=

lim

x

lim

1

= 0,

x→+∞

x

x→+∞ ex

x→+∞ ex

2 −x

2 −x

x2

2x

2

b1 = lim (x e

− 0 · x) = lim x e

=

lim

=

lim

= lim

= 0,

x→+∞

x→+∞

x→+∞ ex

x→+∞ ex

x→+∞ ex

следовательно, y = 0 (при x → +∞ ) – правая горизонтальная асимптота.

k2 =

lim

x2e−x

=

lim

x

lim

1

= ∞,

x→−∞

x

x→−∞ ex

x→+∞ ex

следовательно, при x → −∞ асимптоты нет.

3

2.Общая схема исследования графика функции

Эскиз графика функции можно построить, если знать его характерные особенности. Для этого надо провести следующие исследования:

1.Найти область определения функции.

2.Выяснить, является ли функция четной, нечетной, периодической.

3.Найти точки пересечения графика функции с осями координат.

4.Найти точки разрыва, определить характер разрыва. Выяснить вопрос о существовании асимптот.

5.Найти интервалы возрастания и убывания функции, точки экстремума.

6.Найти интервалы выпуклости функции и точки перегиба.

7.Построение графика функции.

Пример 7. Построить график функции

	y =		x		.
			x − 1
	Решение. Будем следовать изложенной выше схеме:
	1. x =6 1. x (−∞, 1) (1, +∞), т. к.
	y(−x) =	−x			=	x
		−x − 1				x + 1

и, следовательно, y(−x) =6 y(x) и y(−x) =6 −y(x).

2. Функция не является четной, нечетной, периодической.

3.	y = 0 x = 0, график проходит через начало координат.
4.	x = 1 точка разрыва 2-го рода.
	lim	x	= +∞,	lim	x	= −∞.
	x→1+0 x − 1			x→1−0 x − 1

Прямая x = 1 является вертикальной асимптотой. Выясним, существуют ли наклонные

асимптоты.		x		x
	k = lim		= 0, b = lim			= 1.
	x→∞ (x − 1)x		x→∞ x − 1

Итак, прямая y = 1 является горизонтальной асимптотой.

5. Найдем экстремумы функций и интервалы возрастания и убывания. Имеем

y′ =

x − 1 − x

= −

1

< 0,

(x − 1)2

(x − 1)2

следовательно, функция убывает на (−∞, 1),

(1, +∞), точек экстремума нет.

6. Найдем интервалы выпуклости и точки перегиба:

y′′ = −(x − 1)2

′

= (x − 1)3 .

1

2

y′′ > 0

x > 1. Следовательно, при x (1, +∞) график функции выпуклый вниз.

y′′ < 0

x < 1. Следовательно, при x (−∞, 1) график функции выпуклый вверх.

4

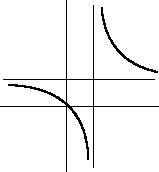
7. Используя полученные данные, строим график функции.

y

6

1

-

0 1 x

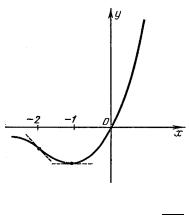
Пример 8. Построить график функции y = 3xex .

Решение.

1.Функция определена всюду на интервале (−∞, +∞).

2.y(−x) = −3xe−x , тогда y(−x) 6= y(x) и y(−x) 6= −y(x), функция не является ни

четной, ни нечетной. Функция непериодическая.

3.Найдем точки пересечения с осями координат. Когда x = 0, то y = 0 и график проходит через начало координат.

4.Функция точек разрыва не имеет, т. к. функция непрерывна. Вертикальных асимптот нет.

Выясним, существуют ли наклонные асимптоты y = kx + b;

k =

lim

y(x)

=

lim

3xex

= 3

lim

x

= ∞.

e

x

x

x→+∞

x→+∞

x→+∞

При x → +∞ наклонных асимптот нет

k =

lim

y(x)

=

lim

3xex

= 3

lim

x

= 0.

e

x

x

x→−∞

x→−∞

x→−∞

b

lim (y(x) − kx) =

lim

3xex = 3

lim

x

=

∞

= 3

lim

1

= 0.

= x→−∞

x→−∞

x→−∞ e−x

∞

x→−∞ e−x

(при вычислении мы использовали правило Лопиталя). При x → −∞ график имеет левую горизонтальную асимптоту y = 0.

5. Найдем экстремумы функций и интервалы возрастания и убывания. Имеем y′ = 3(xex)′ = 3ex(x + 1), y′ = 0 при x = −1.

Точка x = −1 разбивает числовую ось на промежутки (−∞; −1) и (−1, +∞), причем y′ < 0 при x (−∞; −1), поэтому функция на этом промежутке убывает; y′ > 0 при x (−1; +∞) – функция на этом промежутке возрастает.

Точка минимума x = −1 , ymin(−1) = −3e−1.

6. Найдем интервалы выпуклости функции и точки перегиба: y′′ = 3(ex(x + 1))′ = 3ex(x + 2),

y′′ = 0 при x = 2. При x (−∞; −2), y′′ < 0, поэтому график функции на этом промежутке выпуклый вверх. При x (−2; +∞) , y′′ > 0 график функции на этом промежутке выпуклый вниз; x = −2 точка перегиба,

y(−2) = 3(−2)e−2 = −6e−2.

7. Используя полученные данные, строим график функции.

5

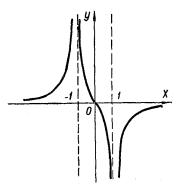
Пример 9. Построить график функции y = ln |xx−+11 |.

Решение.

1.Функция определена на интервалах x (−∞, −1) (−1, 1) (1, +∞).

2.Функция является нечетной, т. к.

y(−x) = ln

−x − 1

= ln

−(x + 1)

= ln x − 1

= − ln x − 1

,

x

x

x

x

− + 1

−( − 1)

+ 1

+ 1

т.е. y(−x) = −y(x), значит, функция симметрична относительно начала координат.

3.Точки пересечения с осями координат x = 0; y = 0.

4. Функция имеет разрыв в точках x = −1 и x = 1,

lim

x − 1

∞

lim

x − 1

∞.

x

= +

= +

x→−1 ln

; x→+1 ln x

+ 1

+ 1

x

, x

являются вертикальными асимптотами.

Прямые

= −1

= 1

Выясним, существуют ли наклонные асимптоты y = kx + b;

ln

x−1

x

− 1

1

x

k

lim

x+1

= ln lim

= ln 1 = 0

= x→∞

x→∞

x

x

+ 1

x − 1

x − 1

b = lim (y(x) − kx) = lim ln |

| = ln lim |

| = ln 1 = 0,

x + 1

x + 1

x→∞

x→∞

x→∞

y = 0 горизонтальная асимптота.

5. Найдем интервалы возрастания, убывания функции, экстремумы функции. Для этого найдем первую производную

x + 1

x − 1

2

y′ =

ln

x − 1

′

·

′

x + 1

=

x − 1

x + 1

=

x2 − 1

,

y

′

=6 0

, следовательно ни в

одной точке данная функция не имеет экстремумов.

В точках x = −1 и

x = 1 производная функции и сама функция не определены.

Точки x = −1 и x = 1 разбивают числовую ось на промежутки: при x (−∞; −1) (1; +∞), y′ > 0 функция возрастает, при x (−1; 1), y′ < 0 функция убывает.

6. Найдем интервалы выпуклости функции и точки перегиба. Для этого найдем

вторую производную.
2			4x
y′′ =		=		.
	x2 − 1		(x2 − 1)2
y′′ = 0 при x = 0. При x (−∞, −1) (−1, 0),			y′′ > 0 , тогда график функции на этом

интервале выпуклый вниз. При x (0, 1) (1, +∞), y′′ > 0 , тогда график функции на этом интервале выпуклый вверх.

7. Строим график функции.

6

7