kurs_lekcii_mo_matematicheskomu_analizu / Замечательные пределы

ЛЕКЦИЯ 4. ЗАМЕЧАТЕЛЬНЫЕ ПРЕДЕЛЫ. СРАВНЕНИЕ БЕСКОНЕЧНО МАЛЫХ. ОДНОСТОРОННИЕ ПРЕДЕЛЫ.

1.Первый замечательный предел

	Справедливо равенство	sin x
	lim		= 1.	(1)
		x
	x→0

Равенство (1) называется первым замечательным пределом. Докажем это равенство.

	Предварительно докажем неравенство
	sin x < x < tg x (0 < x <						π	),	(2)
							2
	для чего в круге радиуса R рассмотрим острый угол AOM , хорду AM и касательную
	AB окружности в точке A .
		y
		6
	'$
		R	%		B
		M%
		xA
		%	A		-	x
		&%
		O N			A

Тогда

площадь AOM < площадь сектора AOM < площадь AOB.

Если через x обозначить радианную меру угла AOM так, что длина дуги AM выразится произведением Rx , то эти неравенства перепишутся в виде

1

R2 sin x <

1

R2x <

1

R2 tg x.

2

2

2

Отсюда, после сокращения на

1 R2 , приходим к неравенствам (2). В предположении,

2

что 0 < x < π/2 , разделим (2) на sin x, получим

x

1

1 <

<

sin x

cos x

или, перевернув неравенство,

sin x

cos x <

< 1,

(3)

x

или

sin x

1 >

> cos x.

x

Откуда

0 < 1 − sinx x < 1 − cos x

1

(умножили последнее неравенство на минус

1 и

прибавили 1 ко всем его

частям).

Заметим, что

x

x

1 − cos x = 2 sin2

< 2 sin

< x.

2

2

Здесь использовано доказанное неравенство (2).

Пусть 0 < x < π . Следовательно, 0 < 1 −

sin x

< x. Отсюда вытекает неравенство

x

2

|

sin x

− 1| < |x| , которое сохранится и при изменении знака x (т. к. cos x ,

sin x

четные

x

x

функции), т. е. неравенство будет справедливо для x =6 0 и |x| < π .

2

Полученное неравенство решает вопрос. Действительно, задавшись произвольным

	ε > 0 , за δ выберем наименьшее из чисел ε и					π : при |x| < δ справедливо |				sin x	− 1| < ε.
						2		sin x		x
	По определению предела функции это и означает, что функция								при стремлении x к
								x
	0 имеет предел 1.
	Можно рассуждать иначе, переходя к пределу в (4), получим
		lim cos x < lim		sin x			< lim 1.
		x→0	x→0			x	x→0
	Так как lim cos x = lim 1 = 1, то по теореме 11
	x→0	x→0
		lim	sin x			= 1.
			x
		x→0

Пример 1. Найти lim

sin ax

.

x→0

x

Решение. Сделаем замену ax = y, тогда x = y

,

a

lim

sin ax

= lim

sin y

= lim a

sin y

= a

x

y

y

x→0

y→0

a

y→0

Следовательно,

sin ax

lim

= a.

x→0

x

В частности, при a = 2

sin 2x

lim

= 2.

x→0

x

Если x → 0, то и y → 0, поэтому

lim sin y = a · 1 = a.

y→0 y

(4)

Пример 2. Найти предел функции lim

sin ax

.

x→0 sin bx

Решение. Разделим числитель и знаменатель на x,

на основании формулы (5)

получим

lim sin ax

sin ax

sin ax

a

lim

= lim

x

=

x→0

x

=

.

sin bx

sin bx

lim sin bx

b

x→0

x→0

x

x→0

x

Следовательно,

sin ax

a

lim

=

.

(5)

x→0 sin bx

b

В частности, при a = 2, b = 5

sin 2x

2

lim

=

.

5

x→0 sin 5x

2

Пример 3.

Найти lim

tg x

.

x→0

x

sin x

Решение. Принимая во внимание, что tg x =

и

lim cos x = cos 0 = 1, тогда на

cos x

x→0

основании свойств пределов получим

x

cos x

=

x→0

x

x→0

cos x

= x→0

x

lim

tg x

= lim

sin x

·

1

lim

1

·

sin x

= lim

1

· lim

sin x

= 1 · 1 = 1.

x→0 cos x

x→0

x

Итак,

tg x

lim

= 1.

x→0

x

sin2 x

Пример 4.

Найти lim

3

.

x2

x→0

Решение. На основании свойств пределов, а также формулы (5) получим

sin2 x

= x→0

sin x

2

sin x

2

1

2 1

x→0 x2

x

x→0 x

= 3

9

lim

3

lim

3

=

lim

3

=

.

Пример 5.

Найти lim

arcsin x

.

x→0

x

y, тогда

x

= sin y

Решение. Сделаем замену

arcsin x =

Следовательно,

arcsin x

y

1

1

lim

= lim

= lim

=

sin y

lim sin y

x→0

x

y→0 sin y

y→0

y

y→0 y

Пример 6.

Найти lim

cos(πx/2)

.

x→1

1 − x

Решение. Сделаем замену

1 − x

= z. Тогда

x = 1 − z

Следовательно,

иy → 0 при x → 0.

=1.

иz → 0 при x → 1.

lim

x→1

Более простой метод

cos π x	= z→0	cos π − π z				sin π z	=	π
1 − x		2	z		z→0 z			2
2	lim		2		= lim	2			.

решения подобных примеров будет рассмотрен ниже.

2.Второй замечательный предел

Ранее была получена формула

lim 1 + 1 n = e,

n→∞ n

или

1

lim (1 + z) z = e.

z→0

Эта формула носит название второго замечательного предела и используется для вычисления неопределенности вида 1∞.

3

x/3

Пример 7.

Найти предел

lim

1 + 6 .

x

→∞

Решение. При x → ∞,

x

6

∞

Сделаем замену x = 6y . Тогда

1 + x

→ 1,

следовательно, имеем неопределенность 1

.

x→∞

x/3

y→∞

y

2y

=

y→∞

y

2

1 + x

y

=

lim

6

= lim

1 +

1

lim

1 +

1

e2.

x

Пример 8.

Найти предел

lim

x+1

.

x−1

Решение.

x→∞

основания

равен

1

(разделите числитель

В

этом

примере

и знаменатель

на

x ),

а показатель степени

стремится

к

бесконечности, имеем

неопределенность вида 1∞ . Для того чтобы раскрыть эту неопределенность, представим основание степени в виде 1 + z , а в показателе выделим множитель 1/z :

x→∞

x − 1

x

x→∞

x − 1

x

x

x→∞ 1 + x − 1

=

lim

x + 1

= lim

1 +

x + 1

− 1

= lim

2

= "x→∞

x−1

#

2x

x − 1

x−1

2

2

lim

2

= e2.

lim

1 +

= ex→∞

1−1/x

Переходя к пределу в квадратной скобке, получаем число e , так как z = x → ∞ .

Пример 9. Найти предел lim

ln(1+x)

.

x→0

x

Решение. Применяя свойства логарифмической функции, получим

ln(1 + x)

1

1

=

ln(1 + x) = ln(1 + x) x ,

x

x

тогда находим

x→0

ln(1 + x)

x→0 h

1

1

i

x

i

hx→0

lim

= lim ln(1 + x) x = ln lim(1 + x) x

= ln e = 1.

Таким образом,

lim

ln(1 + x)

= 1.

x

x→∞

2 → 0 при

x−1

3.Сравнение бесконечно малых

Рассмотрим отношение двух бесконечно малых α(x) и β(x) при x → a (для краткости их будем обозначать α, β ).

Выделим три случая.
1. lim	α	= 0.
x→a β
В этом случае говорят, что			α бесконечно малая (б. м.) более высокого порядка,
чем β , и обозначают α = o(β) .
Пример 10. При x → 2 функция						(x − 2)3 б. м. более высокого порядка, чем
x − 2 , т. к.				(x − 2)3
		lim				= lim(x − 2)2 = 0.
				x − 2
		x→2				x→2

4

	2.	lim	α	= A =6 0.
		x→a β
	В	этом случае функции α и β				называются б. м. одного		и того же порядка и
обозначаются α = O(β) . Так функции sin 2x, sin 5x б. м. одного порядка.
	3.	lim	α	= ∞.
		x→a β
	В этом случае говорят, что α б. м. более низкого порядка, чем β. Можно сказать
также, что β бесконечно малая более высокого порядка, чем α .
	Пример 11. При x → −1 функция x + 1 б. м. более низкого порядка, чем
(x − 1)(x + 1)2 , т. к. lim					(x + 1)		= ∞.
				x→−1 (x − 1)(x + 1)2
	Определение 1. Если функции					α и β одного и того		же порядка, причем
lim	α	= 1 , то они называются эквивалентными бесконечно малыми. Символически это
x→a	β
записывается так: α β.
	Как следует из первого замечательного предела, sin x и x							при x → 0 являются

эквивалентными бесконечно малыми sin x x . Также ранее было показано lim tg x = 1,
следовательно tg x x.						x→0 x
Пример 12. Доказать, что при x → 0 бесконечно малые arctg cx						и cx являются
эквивалентными.
Решение. Положим arctg cx	= z,	тогда	tg z		= cx и z → 0	при x → 0.
Следовательно,	arctg cx		z
lim		= lim			= 1,
	cx
x→0		z→0 tg z

что и требовалось доказать.

Можно доказать эквивалентность следующих бесконечно малых функций при x → 0 :

1.	sin x x.	2.	tg x x.
3.	arcsin x x.	4.	arctg x x.
5.	ln(1 + x) x.	6. ex − 1 x.
7.	(1 + x)a − 1 ax.	8.	1 − cos x	x2	.
			2

При вычислении пределов иногда удобно от одних б. м. величин переходить к их эквивалентным б. м.

Пример 13.

Найти lim

x sin 6x

.

(arctg 2x)2

x→0

Решение. Так как sin cx cx и arctg cx cx, тогда

lim

x sin 6x

= lim

x

·

6x

=

1

· 3 =

3

.

2x

2

2

x→0 (arctg 2x)2

x→0

2x

Пример 14.

Найти lim

ln(x2 − 5x + 7)

.

x→3

x − 3

00 , так как x2 − 5x + 7 → 1

Решение. При x → 3 получаем неопределенность типа

и ln(x2 − 5x + 7) → 0. Выражение x2 − 5x + 7 можно представить так: x2 − 5x + 7 = 1 + (x2 − 5x + 6).

5

Тогда

ln(x2 − 5x + 7) = ln(1 + (x2 − 5x + 6)) x2 − 5x + 6.

Отсюда

	lim	ln(x2 − 5x + 7)		= lim	x2 − 5x + 6	= lim	(x − 2)(x − 3)		=
		x − 3			x − 3		x − 3
	x→3			x→3		x→3

= lim(x − 2) = 1.

x→3

4.Односторонние пределы

Введем понятие одностороннего предела.

Определение 2. Число B называется правым пределом (левым пределом) функции y = f (x) в точке a , если для любого положительного числа ε найдется отвечающее ему положительное число δ такое, что для всех значений аргумента x , удовлетворяющих условию a < x < a + δ (условию a − δ < x < a ), справедливо неравенство |f (x) − B| < ε.

Для обозначения правого (левого) предела функции f (x) в точке a используют следующую символику:

lim f (x) = B ( lim f (x) = B).

x→a+0

x→a−0

Или более кратко: f (a + 0) = B (f (a − 0) = B).

Теорема 1. Для того чтобы функция f (x) имела предел в точке a , необходимо и достаточно, чтобы существовали оба односторонние предела и их значения совпадали.

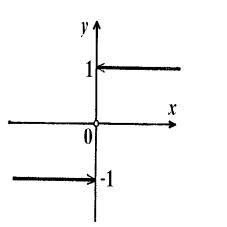
Пример 15. Рассмотрим функцию

+1, если x > 0,

f (x) = sgn(x) = 0, если x = 0,

−1, если x < 0

( sgn(x) латинское название ¾signum¿ знак x). Ее график имеет вид.

6

Эта функция имеет в точке a = 0 как правый, так и левый пределы, причем sgn(0 +

	0) = +1, sgn(0 − 0) = −1. Но они не совпадают, так что					lim sgn x не существует.
						x→0
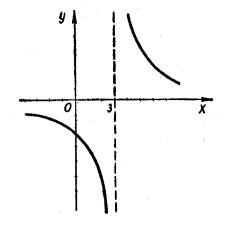
	Пример 16. Найти левый и правый пределы функции f (x) =						6		при x → 3 .
							x−3
	Решение. Задача сводится к нахождению двух пределов
	lim	6	и	lim	6	.
	x→3−0 x − 3			x→3+0 x − 3

Если x → 3 −0, т. е. x стремится к 3, оставаясь меньше 3, то величина x −3 является бесконечно малой, принимающей отрицательные значения. Обратная ей величина будет бесконечно большой, принимающей также отрицательные значения, тем же свойством

обладает и величина y = 6 , поэтому

x−3

6

lim = −∞.

x→3−0 x − 3

Если x → 3 + 0, т. е. x стремится к 3, оставаясь больше 3, то величина x −3 является

положительной бесконечно малой. Обратная ей величина 1 будет бесконечно большой,

x−3

принимающей положительные значения.

				lim	6		= +∞.
				x→3+0 x − 3
	График функции y =	6		имеет вид, указанный ниже.
		x−3

7

Пример 17. Найти левый и правый пределы функции f (x) = e1/(x−a) при x → a .

Решение. Если x → a − 0 , то 1/(x − a) → −∞ и				1			. Если x → a + 0 ,
				lim e		= 0
					x−a
				x→a−0
то 1/(x − a) → ∞ и	1		= ∞ .
	lim e
		x−a

x→a+0

8