Глава 4. Элементы спек­траль­ного анализа

ДИСКРЕТНЫХ СИГНАЛОВ

4.1. Дискретное преобразование Фурье

4.1.1. Оценивание параметров полигармонических

моделей и задачи спектрального анализа

Пусть – наблюдения действительного дискретизован­ного сигнала, представляю­щего собой сумму гармонических (узкополосных) составляю­щих, N – число наблюдений, T – интервал дискрети­зации. Рассмотрим для подобного сигнала на ограниченном временном интервале модельную полигар­моническую функцию вида

(4.1.1)

Вектор параметров для этой модели имеет размерность . Будем полагать, что имеет место случай, когда L – число составляющих в сигнале – известно из априорных сведений.

Для решения задачи оценивания параметров модели (4.1.1) необходимо сформировать функционал , являющийся мерой близости наблюдений и модели, который записыва­ется известным образом:

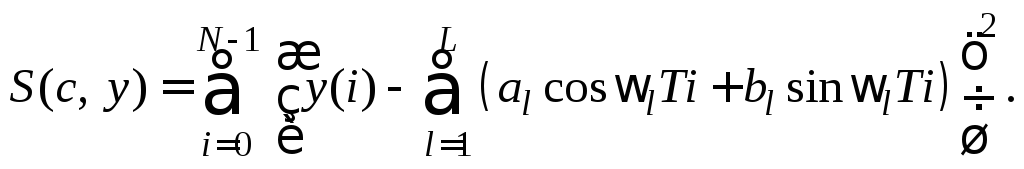(4.1.2)

Оценивание оптимального вектора параметров полигармонической модели сводится к решению задачи минимизации сформированного функционала

.

Нахождение оптимального вектора параметров осуществляется на основе решения достаточно сложной задачи поиска минимума функционала Проблемы определения минимума функционала (4.1.2) обусловлены спецификой модели (4.1.1), представляющей собой сумму синусоидальных функций, нелинейно зависящих от частотных параметров . В силу указанных особенностей модели функционал является многоэкстремальным.

Применим технологическое упрощение в задаче минимизации рассматриваемого функционала, заключающееся в разделе­нии параметров, входящих в модель (4.1.1) линейно и нелиней­но. Нелиней­ные параметры фиксируются и находятся частично оптимальные линейные параметры с помощью решения соответствующей системы линейных уравнений. Вычисляется значение частично оптимального функционала при фиксированных нелинейных параметрах и частично оптимальных линейных параметрах. Далее производится поиск минимума частично оптимального функционала по нелинейным параметрам, позволяющий получить окончательное решение.

Поясним методику реализации предлагаемого технологического упрощения. Положим, что - вектор размерности состоящий из параметров, входящих в модель линейно; – вектор размерности состоящий из нелиней­ных параметров. Введём векторную базисную функцию размерности состоящую из синусоидальных функций

Модель полигармонического сигнала в таком случае можно будет записать в виде скалярного произве­дения

Оптимизируемый функционал оказывается квадратичной формой от линейных параметров :

(4.1.3)

Фиксируем частотные параметры для функционала (4.1.3) и на первом этапе оптимизации находим частично оптимальные линейные параметры из решения системы линейных уравнений

Записываем выражение для вычисления значений частично оптимального функционала

и на втором этапе оптимизации на его основе находим оптимальные нелинейные частотные параметры путём подпоиска по частотным параметрам для частично оптимального функционала. Необходимо отметить, что функционал является многоэкстремальным. Оптимальные линейные параметры являются функциями оптимальных частотных параметров

Описанное технологическое упрощение, очевидно, эффек­тивно лишь при малой размернос­ти вектора нелиней­ных параметров.

Вычислительные трудности оптимизации сформи­рованно­го функционала происходят от того, что для достижения доста­точно высокой точности подгон­ки модели к наблюде­ниям осуществля­ется подпоиск многоэкстремального функционала по частотным нели­ней­ным парамет­рам. Проблемы решения задачи оценивания параметров полигармонической модели многократ­но увеличива­ются, если оказывается неизвес­тным число гармонических (узкополосных) составля­ющих в наблюдениях сигнала.

Оценивание параметров полигармонических моделей применяется для решения одного из вариантов задачи спектрального анализа – определения оценок амплитуд и частот составляющих в наблюдениях.

4.1.2. Дискретное преобразование Фурье для действительных сигналов

Один из возможных путей, радикально упроща­ющий задачу оценивания параметров для полигармонических моделей, состоит в подмене исходной задачи на видоизменённую задачу с линейной мо­делью, в которой используются синусои­дальные базис­ные функции с фиксиро­ванными частотами. Частоты базисных функций располагаются равномерно на частотной оси с достаточно мелким шагом; как правило, число синусоидальных базисных функций в модели должно быть много больше числа частот­ных составляю­щих в наблю­дени­ях.

Перейдём к рассмотрению дискретного преобразования Фурье (ДПФ) для действительных сигналов. Так же как и в разд. 4.1.1, являются наблюдениями действительного дискретизованного сигнала, N – число наблюдений, T – интервал дискрети­зации. В самом общем случае для ДПФ не выдвигается никаких специальных требований к наблюдениям сигнала.

Полигармоническую модель с фиксированными частотами для ДПФ в действительном случае примем в следующем виде:

(4.1.4)

Указанные частоты для модели (4.1.4) подчиняются соотношениям:

Вектор параметров модели имеет размерность Оптимизируемый квадратичный по функционал записывается по аналогии с (4.1.2):

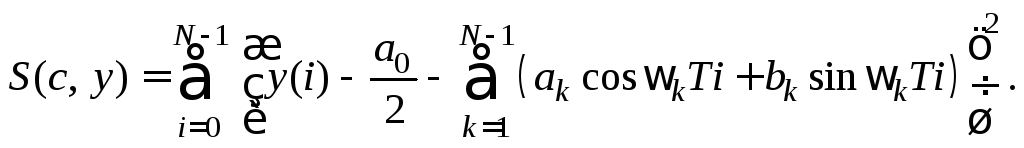(4.1.5)

Оценки параметров для модели (4.1.4) находятся из решения задачи минимизации функционала

(4.1.6)

Для модели (4.1.4) введём векторную базисную функцию размерности :

Обратим внимание на то, что благодаря выбранным частотам данная векторная базисная функция не зависит от интервала дискрети­зации T:

Модель (4.1.4) и функционал (4.1.5) могут быть представлены с использованием скалярных произведений

(4.1.7)

Введем на основе материалов разд. 2.4 векторно-матричные обозначения для вектора наблюдений Y размерности вектора параметров размерности и матрицы плана сигнала X размерности :

, ,

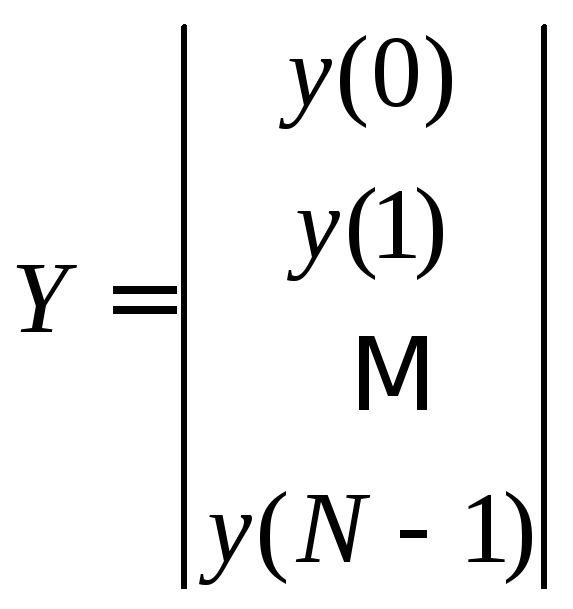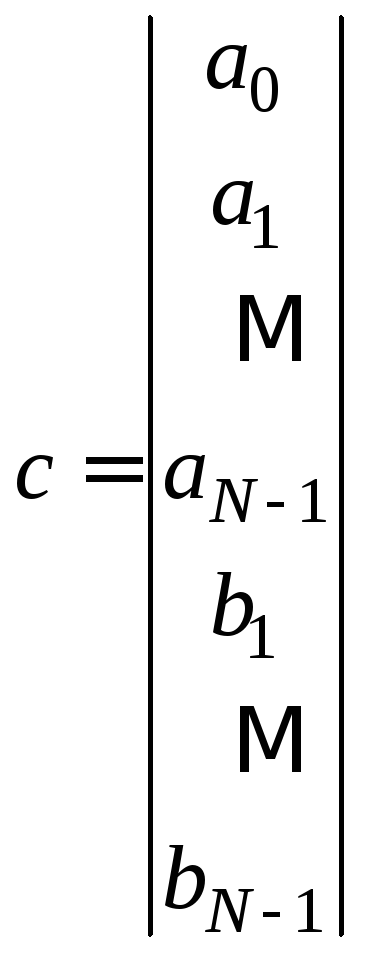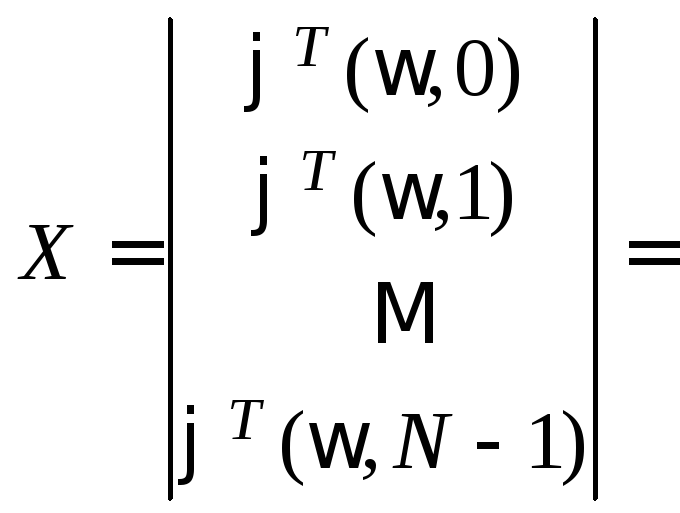
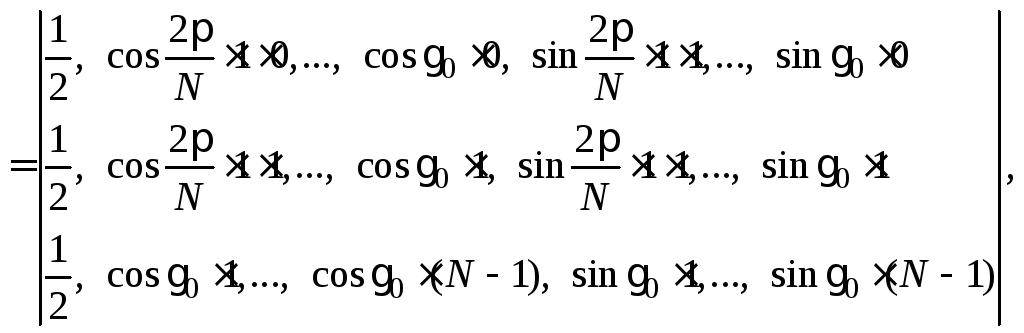
где

Оптимизируемый квадратичный по функционал запишется с помощью векторно-матричных обозначений в виде скалярного произведения, тождественно совпадающего с функционалом (4.1.5), (4.1.7)

Оценки параметров модели соответствующие задаче минимизации (4.1.6), могут быть вычислены с помощью формулы (2.4.7)

Рассмотрим скалярные произведения синусоидальных базисных функций Благодаря предложенному расположению частот в модели введённые базисные функции являются ортогональными

и

В этом можно убедиться, если произвести вычисления скаляр­ных произве­дений для базисных функций на основе использования табличных формул для тригонометрических сумм. В самом деле, вычислим скалярные произведения базисных функций для разных индексов

для

Вычислим скалярные произведения базисных функций для одинаковых индексов:

Вследствие ортогональности введённых синусоидальных базисных функций матрица размерности является диагональной:

, .

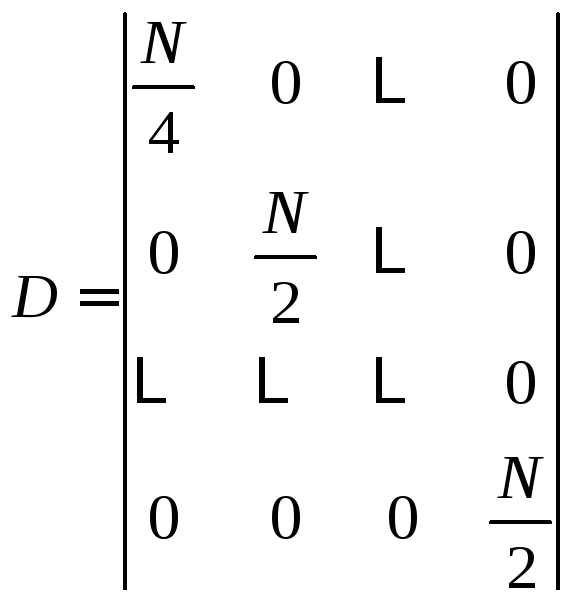Вектор коэффициентов Фурье размерности представляет собой набор скалярных произведений вида

,

,…,

Оптимальные параметры модели для ДПФ выразятся через коэффициенты Фурье

(4.1.8)

Основываясь на (4.1.8), запишем формулы, определяющие оптимальные параметры для модели (4.1.4) и являющиеся коэффи­ци­ентами ДПФ для случая действи­тельных наблюдений и действительной модели:

(4.1.9)

В формулах (4.1.9) опущен знак оптимальности В соответствии с (4.1.9) ДПФ осуществляет линейное преобразование вектора наблюдений сигнала размерности в вектор параметров модели размерности

4.1.3. Дискретное преобразование Фурье для комплексных сигналов

Обобщим ДПФ, предложенное в разд. 4.1.2, для комплексных сигналов. Пусть – комплексные наблюдения, Введём комплексную модель для наблюдений в точках

Для этой модели – комплексные параметры, W – корень N-й степени из единицы, – комплексные базисные функции, :

Функционал – мера близости комплексных наблюде­ний и модели, запишется с помощью суммы комплексно-сопряженных сомножителей

. (4.1.10)

Введём комплексные векторно-матричные переменные – вектор ком­плек­сных наблюде­ний Y размер­ности (N, 1), вектор комплек­сных параметров модели размер­ности (N, 1) и комплексную матрицу плана сигнала X размер­ности (N, N):

, ,

_.

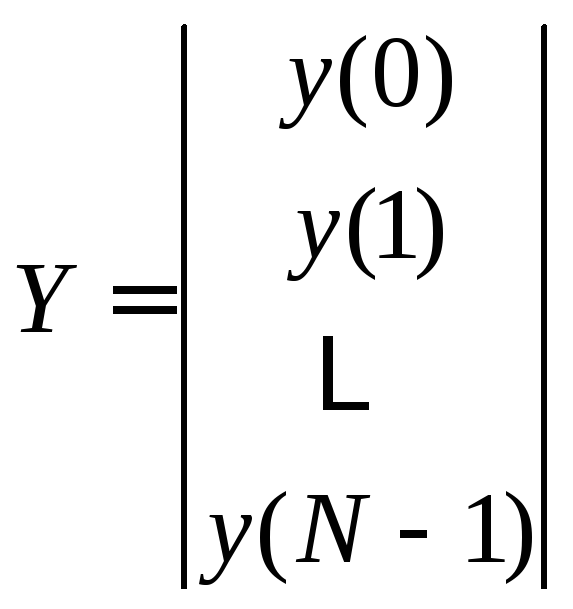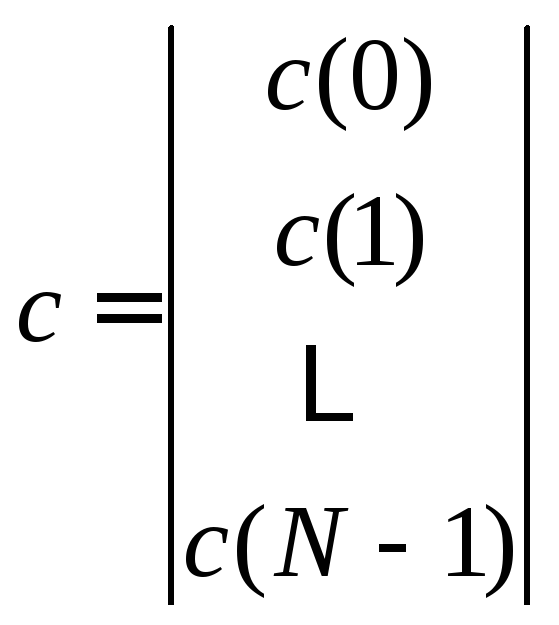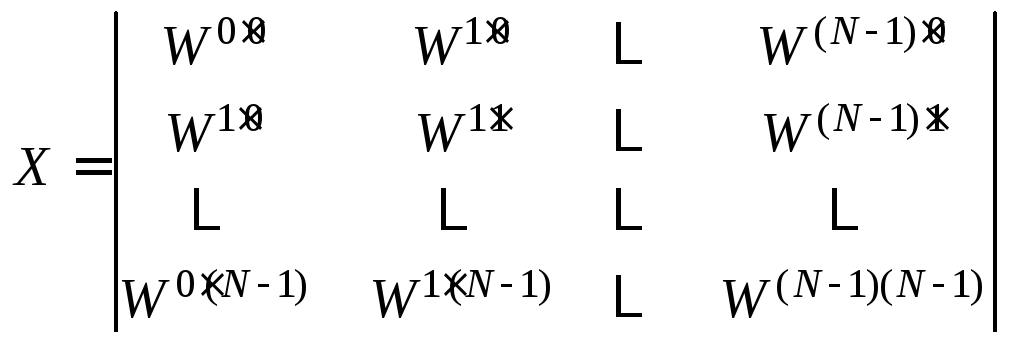С учётом сопряжённости, основываясь на (2.4.9), запишем выражение для оптимальных оценок параметров

Матрица и вектор коэффи­циентов Фурье выразятся с использованием комплек­сных сопряже­ний. Коэффициенты ДПФ находят­ся из системы

Базисные комплексные синусоидальные функции ортого­нальны, и поэтому матрица D диаго­наль­на. Вычис­лим коэффициенты этой матрицы, сформи­ровав тригоно­метрические суммы, являющиеся скаляр­ными произве­дениями для столбцов комплек­сной матрицы плана сигнала:

Для индексов имеем для следует, что Тогда нетрудно видеть, что

, ,

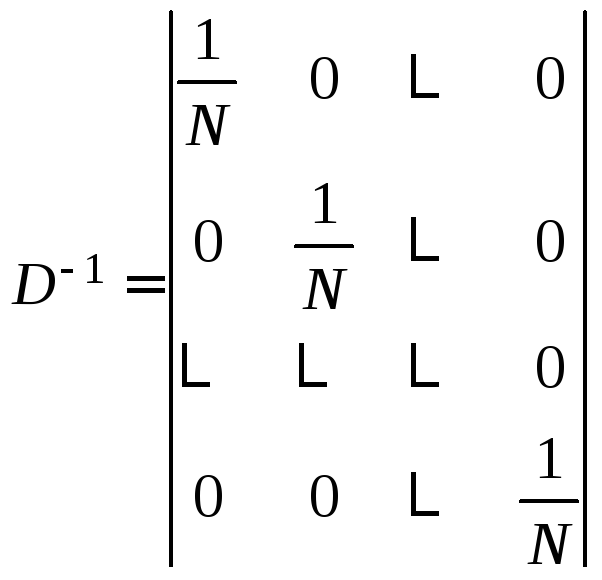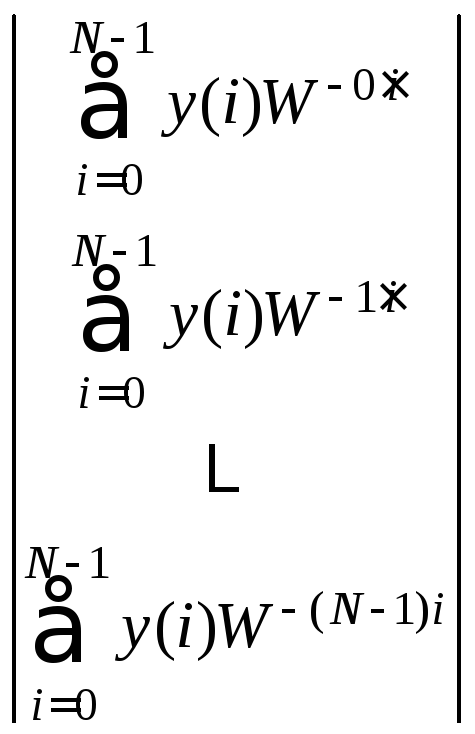Коэффициенты ДПФ для случая комплексных наблюдений и комплексной модели запишутся следующим образом:

, (4.1.11)

где так же, как и в (4.1.9), опущен знак оптимальности.

Вычислим остаточную сумму для оптимальных коэффи­циентов комплексного ДПФ. Подста­вим под знак суммы (4.1.10) получен­ные выражения для коэффициен­тов :





Рассмотрим отдельно выражение в скобках под знаком суммы, переставим порядки суммирования, учитывая, что

для для

Нетрудно видеть, что имеет место равенство Остаточная сумма для функционала (4.1.10) на опти­маль­ных коэффициентах ДПФ равняется нулю – предлагаемая тригонометри­ческая модель с нулевой погрешностью аппрокси­мирует наблюдения. Благодаря этому обстоятельству можно записать формулы прямого и обратного дискретного преобра­зова­ния Фурье, физический смысл которых очевиден

Приведём показа­тельную форму для комплексного ДПФ. Определим амплитуды и фазы составляющих ДПФ в зависимости от дискретного номера k:

Результаты вычисления составляющих ДПФ можно графически изображать в виде амплитудного и фазового спектров. Для удобств изображений амплитудных спектров применяется логарифмический масштаб:

Вполне правомерно введение зависимости от частоты для составляющих спектра ДПФ. Шаг дискретности по частоте для составляющих определяется интерва­лом наблюдения NT, Составляющие спектра – амплитуды и фазы модельных комплексных синусоид – распола­гаются равно­мер­но по оси частот, , где так же, как и разд. 4.1.2,

Рассмотрим пример вычисления амплитудного и фазового спектра ДПФ для сигнала в виде единичного прямоугольного импульса:

для для (4.1.12)

Нахождение ДПФ для данного сигнала сводится к суммированию комплексной геометрической прогрессии со знаменателем :

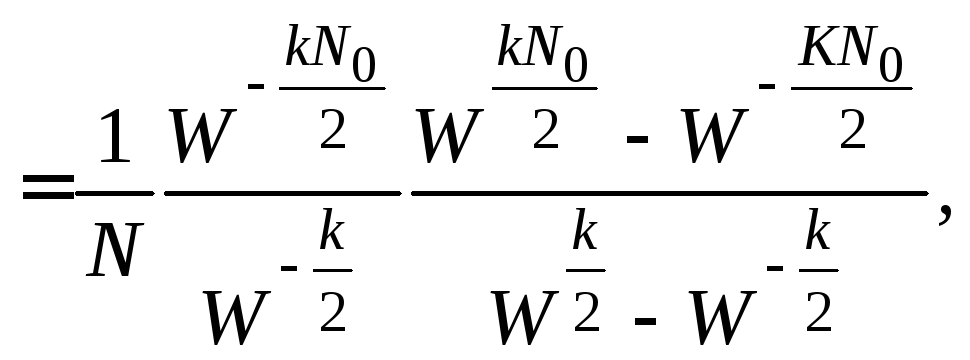
Cделаем необходимые выкладки, чтобы получить формулы для значений амплитудного и фазового спектров

,

, ,

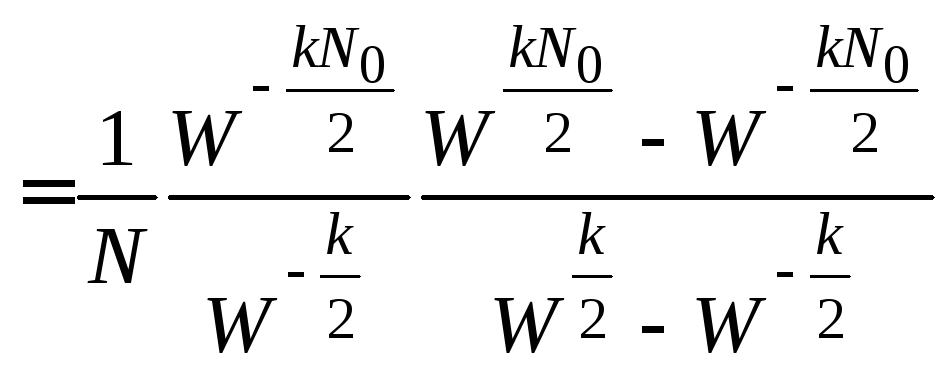
(4.1.13)

Для расчётов по формулам (4.1.13) взяты значения На рис. 4.1.1 изображен логарифмический амплитудный спектр ДПФ сигнала (4.1.12) для точек

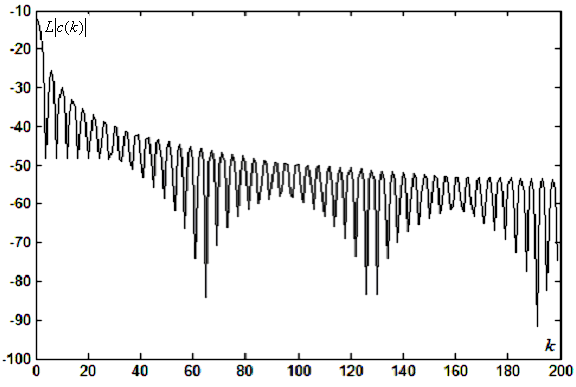
Рис. 4.1.1. Логарифмический амплитудный спектр ДПФ

для прямоугольного импульса

В практике обработки дискретных наблюдений, как правило, приходится иметь дело с действитель­ными сигналами. Однако многие программы алгоритмов вычисле­ния коэффи­циентов ДПФ ввиду опреде­лённых удобств записыва­ются в комплек­сной форме. Чтобы можно было воспользовать­ся этими програм­ма­ми для вычисления ДПФ действитель­ных сигналов, необходимо положить в комплек­сных наблюдениях мнимую составляющую, равную нулю:

Для комплексного сигнала с нулевой мнимой составляющей проведём вычисления коэффициентов ДПФ, получим

Коэффициенты комплексного и действительного ДПФ связаны простыми соотношениями, которые следует применять для пересчёта:

, , , .