gos / Гетманов3

Глава 5. ДИСКРЕТНЫЕ СВЁРТКИ

5.1. Определения дискретных свёрток

Дискретные свёртки достаточно часто встречаются в различных задачах ЦОС, например при вычислении выходных сигналов линейных динамических систем. Приведём определения для дискретных свёрток, основываясь на предварительных сведениях, помещённых в разд. 1.2.2.

Пусть заданы две последовательности h(i), y(i), определённые в дискретных точках. Первая последовательность h(i) служит ядром свёртки, вторая последовательность y(i) представляет собой дис-

кретные значения входного сигнала. Будем полагать, что дискретные индексы для указанных последовательностей могут принимать значения в заданных диапазонах. Этим двум последовательностям ставится в соответствие выходная дискретная последовательность x(i). Устанавливаются нижние и верхние пределы суммирования в

свёртках S1, S2 и пределы изменения индексов I1, I2 для выход-

ной последовательности. Дискретные свёртки с постоянными и с переменными пределами суммирования представляются формулами

S2

x(i)

s S1

		S2 (i)
h(i s) y(s),	x(i)	h(i s) y(s),	I1 i I2. (5.1.1)

s S1(i)

Свёртка двух бесконечных последовательностей h(i), y(i) определяется следующим образом:

x(i) h(i s) y(s),	i .	(5.1.2)

s

Свёртки типа (5.1.2) называются линейными, их не следует путать с круговыми свёртками для периодических последовательностей, которые будут рассматриваться позже.

Целесообразно отметить существенное обстоятельство для свёрток – различное направление изменения (с разными знаками) индексов сомножителей при суммировании. Задачи, которые воз-

никают при нахождении дискретных свёрток, состоят, в основном,

166

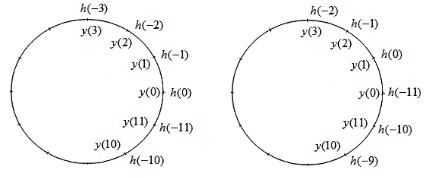
в эффективном вычислении по точности и быстродействию выходной последовательности x(i) для заданных дискретных последова-

тельностей h(i), y(i) с учётом их особенностей.

5.2. Вычисление прямых и обратных круговых свёрток

Перейдём к определению круговых свёрток (прямых круговых свёрток). Пусть заданы дискретные периодические с периодом N последовательности h(i), x(i), i , h(i) h(i N),

y(i) y(i N). По определению дискретная круговая свёртка представляется выражением

N 1

x(i) h(i s) y(s),	i 0, 1,..., N 1.	(5.2.1)
s 0

Процедуру вычисления круговой свёртки удобно наглядно представить на круговых диаграммах, изображённых на рис. 5.2.1а, 5.2.1б в виде систем из внутренней и внешней окружностей, которые могут пошагово вращаться друг относительно друга.

Рис. 5.2.1а. Процедура вычисления	Рис. 5.2.1б. Процедура вычисления
круговой свёртки для i = 0, N = 12	круговой свёртки для i = 1, N = 12
Значения для периодического	входного сигнала y(s),

s 0, 1,..., N 1, располагаются на внутренней окружности данной круговой диаграммы, значения для периодического ядра – на внешней окружности. Нахождение свёртки x(i), i 0, 1,..., N 1, сводится к пошаговому вращению внешней окружности с после-

167

дующим попарным умножением и суммированием. На рис. 5.2.1а, 5.2.1б проиллюстрировано вычисление x(0), x(1) :

N 1	N 1
x(0) h(0 s) y(s),	x(1) h(1 s) y(s).
s 0	s 0

Сделаем в свёртке (5.2.1) замену переменных: i s m. Из равенства s 0 получаем m i; из s N 1 следует m i (N 1).

Тогда на основе изменения пределов суммирования записывается равенство для новой круговой свёртки:

	i ( N 1)
x(i)	h(m) y(i m),	i 0, 1,.., N 1.
	m i

Проанализировав вычисления на представленной круговой диаграмме, нетрудно заметить, что результат суммирования не изменится, если произвольно изменить точку начала и направление суммирования на круговой диаграмме. Справедливо равенство

N 1
x(i) h(m) y(i m).	(5.2.2)

m 0

Круговую свёртку в ряде случаев удобно представлять с по-

мощью введения векторно-матричных переменных:
		x(0)			y(0)
	x	x(1)	,	y	y(1)	,
		x(N 1)			y(N 1)
	h(0),	h( 1),			h( (N 1))
H	h(1 0),	h(1 1),			h(1 (N 1))		, (5.2.3)
	h((N 1) 0)				h((N 1) (N 1))

где выходные и входные векторы x, y имеют размерность (N, 1), матрица свёртки H имеет размерность (N, N). Результат свёртки с

использованием (5.2.3) записывается в виде векторно-матричного произведения x Hy.

Очевидно, что временные затраты на нахождение свёртки, если следовать в вычислениях непосредственно определению (5.2.2),

168

(5.2.3), сравнимы с временными затратами на нахождение ДПФ по прямым формулам.

Рассмотрим алгоритм вычисления круговых свёрток, позволяющий существенным образом уменьшить временные затраты. Возьмём выражение для круговой свёртки (5.2.1), найдем ДПФ от его левой и правой части:

	1	N 1	1	N 1	N 1
		x(i)W ki		W ki h(i s) y(s).
	N i 0		N i 0		s 0

Переставив порядок суммирования, с учётом периодичности, получим

			1		N 1			1			N 1
сx (k)					y(s)W ks N						h(i s)W kiW ks
			N s 0						N i 0
	1	N 1				1	N 1
		y(s)W ks N						h(i s)W k (i s) .
	N s 0					N i 0

Окончательно запишем выражение в частотной области через произведения ДПФ

cx (k) Ncy (k)ch (k),

k 0, 1,..., N 1.

(5.2.4)

Круговые свёртки могут быть вычислены на основе обратного дискретного преобразования Фурье для произведений ДПФ входной последовательности и дискретной последовательности ядра:

N 1
x(i) N cy (k)ch (k)W ki ,	i 0, 1,..., N 1.
k 0

Временные затраты по предлагаемому методу эквивалентны выполнению трёх ДПФ и N комплексных умножений. Выигрыш по времени при вычислении круговых свёрток в частотной области очевиден.

Рассмотрим алгоритм вычисления обратных круговых свёрток. Нахождение свёрток, о которых шла речь, обычно интерпретируется как прямая задача, связанная с определением выходной реакции линейной системы с известной импульсной переходной функцией на заданное входное воздействие. Однако возможна другая постановка, имеющая широкие приложения, состоящая в необходимости определения входного воздействия на линейную систему по известной выходной реакции и известной импульсно-переходной функции – эта задача интерпретируется как обратная.

169

Запишем выражение для дискретной круговой свёртки в скалярном и эквивалентном векторно-матричном виде

	N 1
	x(i) h(i s) y(s),		i 0, 1,..., N 1,	x Hy.
	s 0
Нахождение вектора входного воздействия				на	систему
yT ( y(0),	y(1),..., y(N 1))	по	известному выходному		вектору
xT (x(0),	x(1),..., x(N 1))	и квадратной матрице		свёртки H из

(5.2.3) сводится к решению системы линейных уравнений и записывается в виде y H 1x. Решение подобной задачи во временной

области сопряжено со значительными проблемами – необходимо, чтобы матрица H имела ненулевой определитель – матрица должна быть хорошо обусловленной и размерность этой матрицы должна быть не очень большой, для обеспечения эффективного решения системы линейных уравнений. В большинстве практических задач последнее условие в ряде случаев трудно обеспечить.

Нахождение искомого вектора y, с учётом сказанного, удобно производить в частотной области с использованием процедур ДПФ. Воспользуемся сделанной записью свёртки (5.2.4) на основе ДПФ, выразим ДПФ для искомого входного вектора y через отношение

ДПФ выходного вектора x ДПФ переходной функции – ядра, и далее вычислим обратное ДПФ

	1		cx (k)		N 1	N 1	1		cx (k)
cy (k)				,	y(i) cy (k)W ki					W ki ,
	N c (k)
					k 0	k 0	N c (k)
			h						h
					i 0, 1,...,	N 1.

Предложенное решение задачи – вычисление обратной свёртки в частотной области с точки зрения временных затрат, очевидно, значительно эффективнее процедуры решения во временной области.

5.3. Вычисление апериодических свёрток

Рассмотрим алгоритмы вычисления апериодических свёрток. Пусть последовательности h(i), y(i), входящие в свёртки (5.1.1),

определены в N1, N2 точках, h(i) 0	для i 0,	i N1,	y(i) 0 для
170

i 0,	i N2. Апериодическая	свёртка определяется	следующим
выражением
	i
	x(i) h(i s) y(s),	i 0, 1,..., N1 N2 2.	(5.3.1)

s 0

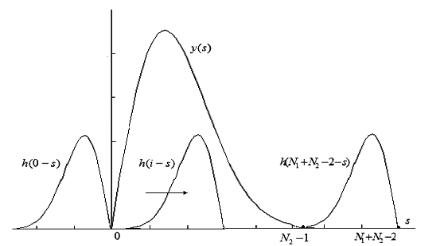
На рис. 5.3.1 схематически изображена процедура вычисления апериодической свёртки, основанный на движении вправо графика функции h(i s) за счёт увеличения индекса i.

Рис. 5.3.1. Процедура вычисления апериодической свёртки

Последовательность x(i) определена в N1 N2 1 точках. Если

раскрыть выражение для апериодической свёртки, то из представ-

ления суммы x(i) h(i) y(0) h(i 1) y(1) ... h(0) y(i) следует воз-

можность следующей записи:

i

x(i) h(s) y(i s).

s 0

Апериодические свёртки могут быть сведены к круговым. Введём последовательности h1(i), y1(i), определённые в N1 N2 1 точках:

h1(i) h(i),	0 i N1 1,	h1(i) 0,	N1 i N1 N2 2,
y1(i) y(i),	0 i N2 1,	y1(i) 0,	N2 i N1 N2 2.
		171

Периодически продолжим последовательности h1(i), y1(i) с периодом N1 N2 1. После доопределения можно убедиться в справед-

ливости записи исходной апериодической свёртки в форме круговой:

	N N	2
x1(i)	1 2	h1(i s) y1(s),	i 0, 1,..., N1 N2 2,

s 0

ивозможности равенства x1(i) x(i).

Сведение апериодических свёрток к круговым в ряде случаев не всегда удобно реализовывать, когда длина одной последовательности много больше длины другой, например при N2 N1. Разобьём

интервал определения свёртки на некоторое число состыкованных участков – локальных интервалов, и вычислим основную свёртку по частям – осуществим секционирование свёртки. Положим, что N1 N2 1 Nm, m – число локальных интервалов; N – число то-

чек на локальном интервале. Последовательность y1(i) разобьём на сумму m подпоследовательностей y1 j (i), j 1,..., m :

y1 j (i) y1(i), N( j 1) i Nj 1,	y1 j (i) 0,
i N( j 1), i Nj 1.

Благодаря такому определению входная последовательность может быть сформирована в виде суммы

m

y1(i) y1 j (i).

j 1

Выпишем выражение для образующихся секционированных свёрток

	Nj 1
x j (i)		h1(i s) y1 j (s),	i N( j 1),..., Nj 1 N1,

s N ( j 1)

j 1,..., m.

Получим окончательный результат – апериодическая свёртка представляется суммой перекрывающихся свёрток

m

x(i) x j (i), i 0, 1,..., N1 N2 2.

j 1

172

Вычисление x j (i) сводится к короткой круговой свёртке размерности N N1 1, нахождение x(i) эквивалентно вычислению m круговых свёрток длиной N N1 1 точек. Видно, что x j (i) определена в N N1 1 точках, тогда как подпоследовательность y1 j (i)

имеет длину N, поэтому суммирование при вычислении исходной свёртки осуществляется с «перекрытием».

Список вопросов для самопроверки к гл. 5

1.В чём состоит определение для круговых свёрток?

2.Каким образом реализуется вычисление круговых свёрток на круговой диаграмме?

3.Каким образом вычисление круговых свёрток сводится к вычислениям ДПФ?

4.В чём состоит отличие определения для апериодических свёрток от определения круговых вёрток?

5.Каким образом вычисление апериодических свёрток сводится

квычислению круговых свёрток?

6.Каким образом реализуется секционирование апериодических свёрток?

173

Глава 6. ЦИФРОВАЯ ФИЛЬТРАЦИЯ СИГНАЛОВ

6.1.Разностные уравнения и импульсно-переходные функции цифровых фильтров

6.1.1. Разностные уравнения цифровых фильтров

Разностные уравнения для цифровых фильтров (ЦФ) задаются соотношениями типа

m	k
x(i) br x(i r) as y(i s),		i 0, 1, 2... .	(6.1.1)
r 1	s 0

В соответствии с (6.1.1), ЦФ осуществляют линейное преобразование входного сигнала в виде скалярной последовательности y(i) y(Ti) , определённой для дискретных индексов k i ,

в выходной сигнал в виде последовательности x(i) x(Ti) ,

m i . Здесь T – интервал дискретизации, хотя в явном виде разностные уравнения (6.1.1) не зависят от T.

ЦФ полностью определяется набором коэффициентов разностного уравнения – весовыми параметрами b1 ,b2 ,...,bm , a0 , a1 ,..., ak ,

и, как следствие, целыми числами m, k , которые задают порядок ЦФ. Формирование выходной последовательности начинают с дискретного индекса i 0 . Значение х(0) вычисляется на основе m

начальных условий		для входной		последовательности x( 1),
x( 2),..., x( m) и	k 1		значений	входной последовательности
у(0), y( 1),..., y( k);		х(1)	для n 1 вычисляется на основе m зна-

чений входной последовательности х(0), x( 1),..., x( m 1) и k 1 значений входной последовательности у(1), у(0),..., y( k 1) и т.д.

Выходной сигнал ЦФ (6.1.1) состоит из суммы сдвинутых и взвешенных значений входного сигнала – скользящего среднего входного сигнала и обратной связи – суммы сдвинутых и взвешенных значений выходного сигнала.

ЦФ делятся на два класса. К первому классу относятся нерекурсивные цифровые фильтры (НРЦ-фильтры) или фильтры скользя-

174

y2 ( )

щего среднего, разностные уравнения для которых представляются соотношением

k
x(i) as y(i s),	i 0, 1, 2... .	(6.1.2)

s 0

Сигнал с выхода таких фильтров не зависит от обратной связи. Ко второму классу относятся рекурсивные цифровые фильтры (РЦфильтры), являющиеся фильтрами общего вида, разностные уравнения для которых определены в (6.1.1); для этих фильтров выходной сигнал зависит от сигнала обратной связи. Следует отметить один частный вид РЦ-фильтров без скользящего усреднения

m
x(i) br x(i r) a0 y(i),	i 0, 1, 2... .

r1

Вкачестве примера приведём разностное уравнение ЦФ первого порядка в виде цифрового апериодического звена

x(i) b1x(i 1) a0 y(i)

(6.1.3)

и разностное уравнение ЦФ второго порядка в виде колебательного звена – цифрового резонатора

x(i) b1x(i 1) b2 x(i 2) a0 y(i).

(6.1.4)

На рис. 6.1.1а приведена иллюстрация выходного сигнала фильтра первого порядка (6.1.3) при действии входного единичного ступенчатого воздействия, полученная в результате математического моделирования. Для расчёта брались значения a0 0,15; b1 0,75;

y(i) 1 для i 0, 1,..., 19 .	Начальное условие x( 1) 0,133. Видно,
что дискретные значения	выходного сигнала фильтра	x(i) для
i 0, 1,..., 19 стремятся	асимптотически к величине	y1( )

a0 / (1 b1) 0,15 / (1 0,75) 0,6. Рис. 6.1.1б содержит изображение выходного сигнала фильтра второго порядка (6.1.4) при дейст-

вии единичного воздействия		y(i) 1 для i 0, 1,..., 34.		При моде-
лировании	для параметров	фильтра были	выбраны	значения
а0 0,55 и	b1 0,95; b2 0,75, начальные		условия	– x( 1)
0,354;	x( 2) 1,6367. Выходной сигнал		x(i), i 0, 1,..., 34,

представляет собой дискретные затухающие колебания, которые стремятся асимптотически к постоянной величине

a0 / (1 b1 b2 ) 0,55 / (1 0,95 0,75) 0, 203.

175