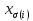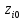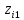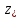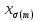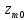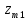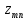- •2.Постановка задачи линейного программирования. Основные формы задачи линейного программирования. Симплекс-таблица и критерий оптимальности. Прямой симплекс-метод и метод искусственного базиса.
- •3.Суть двойственных задач линейного программирования. Теоремы двойственности линейного программирования. Двойственный симплекс-метод.
- •5. Сравнительный анализ эффективности методов решения задач одномерной нелинейной оптимизации без ограничений. Стратегии выбора исходного интервала неопределенности и поиска глобального экстремума.
- •6. Постановка задачи многомерной безусловной оптимизации и классификация методов ее решения. Прямые методы поиска: Гаусса, конфигураций, вращающихся координат, деформируемого многогранника.
- •9. Постановка задачи многомерной безусловной оптимизации и классификация методов ее решения. Методы второго порядка: метод Ньютона и его модификации, методы переменной метрики.
1. Постановка задачи поиска оптимального решения. Основные понятия, используемые при решении задач оптимизации. Классификация задач оптимизации. Суть задач математического программирования и основные трудности при их решении.
Постановка задачи поиска оптимального решения. Основные понятия, используемые при решении задач оптимизации.
Везде
снизу min приписывать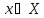 !!!
!!!
(Необходимо определить:)
1)
n-мерное Евклидово
пространство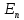
2)
мн-во
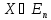
3)
отображение
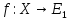
4) критерий оптимизации: минимум либо максимум
Формулировка
задачи:
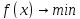 при
при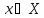 (либо
(либо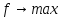 при
при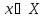 )
)
Решить задачу оптимизации значит. (Пусть ищем min):
1)
найти
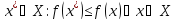 ,
т.е.
,
т.е.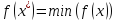 при
при
2)
либо (если не можем найти
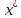 )
найти значение ф-ии
)
найти значение ф-ии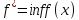 при
при
3) либо доказать, что f(x) не ограничена снизу
4)
либо доказать, что X= ,
т.е. Х является пустым мн-вом
,
т.е. Х является пустым мн-вом
Поиск
max всегда можно свести к поиску min:
 при
при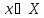
f(x) - целевая ф-ия
X– мн-во допустимых точек, допустимая область
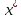 -
глобальный экстремум
-
глобальный экстремум
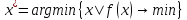 ;
;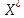 - множество оптимальных точек.
- множество оптимальных точек.
Локальный экстремум (для min):
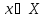 называется локальным экстремумом, если
называется локальным экстремумом, если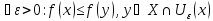
Любой глобальный minявляется локальнымmin.
Если у ф-ии есть лок. экстремумы, то необх. их все найти и выбрать меньший
Задание множества X:
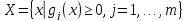
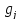 - ограничение, в общем случае
нелинейное
- ограничение, в общем случае
нелинейное
Типы ограничений:
1) Ограничения в виде неравенств
2) Ограничения в виде равенств
Особенности допустимой области Х:
1. 1) Односвязное мн-во (т.е. все точки области модно соединить не выходя за границу)
2) Многосвязное мн-во
2. Выпуклость и вогнутость
Xвыпуклое, если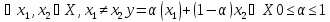
Х-ки ф-ии:
1. Выпуклость и вогнутость
f(x) - выпуклая,
если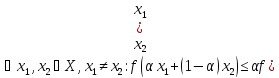
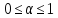
2. Унимодальность (если 1 экстремум)
Методы оптимизации классифицируются в соответствии с задачами оптимизации:
1)Методы одномерной безусловной оптимизации
Ограничений
на доп. область нет, т.е.
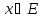
2)Методы многомерной безусловной оптимизации
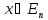 (для унимодальных и многомодальных
ф-ций)
(для унимодальных и многомодальных
ф-ций)
3) Методы линейного программирования
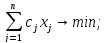
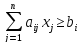 ,
,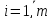 ,
,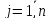 ,
, ,
,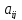 –коэф-ты
–коэф-ты
4) Методы квадратичного программирования
f(x)
явл квартичной, т.е.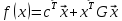
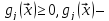 линейные
линейные
5) Методы выпуклого программирования
f(x)–выпуклая,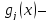 вогнутые
вогнутые
Х–выпуклое мн-во
6) Методы нелинейного программирования
f(x)
– нелин. ф-ия,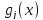 –
нелинейные
–
нелинейные
7) Методы целочисленного программирования
f(x) любая, Х–мн-во целых чисел
Математическое программирование – это математическая дисциплина, в которой разрабатываются методы отыскания экстремальных значений целевой функции среди множества ее возможных значений, определяемых ограничениями.
Особенности решения задач оптимизации с использования численных методов
1) выбор начальной точки – процесс выбора не формализован
2) ошибки вычислений
3)нахождение
оценки экстремумов
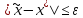 (точные значения найти невозможно)
(точные значения найти невозможно)
Отметим, что решение задач оптимизации будет очень трудоемко при следующих особенностях ф-ии
1) нечувствительность f(x) к значениям каких-то переменных
2) значения f(x) близки к бесконечности
3) овражные функции
2.Постановка задачи линейного программирования. Основные формы задачи линейного программирования. Симплекс-таблица и критерий оптимальности. Прямой симплекс-метод и метод искусственного базиса.
Общая форма ЗЛП (постановка задачи):
 ,
,
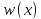 –целевая
ф-ия
–целевая
ф-ия
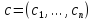 –вектор-строка
–вектор-строка
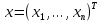 –вектор-столбец
–вектор-столбец
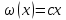
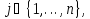 n–размерность
пространства
n–размерность
пространства
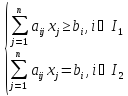 – ограничения Х
– ограничения Х
 ,
,
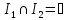
кол-во ограничений m
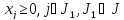 - неотрицательные переменные (остальные
- неотрицательные переменные (остальные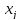 - свободные)
- свободные)
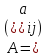 –
матрица mxn
–
матрица mxn
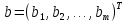 –вектор-столбец
–вектор-столбец
Формы описания ЗЛП
1.общая (приведена выше)
2.каноническая
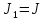 ,
т.е. свободных переменных нет
,
т.е. свободных переменных нет
Все
ограничения в форме равенств (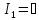 )
)
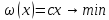

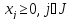
3.стандартная
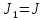
Все
ограничения в форме неравенств (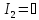 )
)
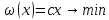
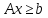
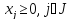
Симплекс-таблица
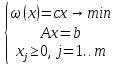
 (–базис)
(–базис)
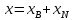 ,
,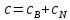
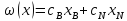
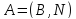
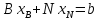
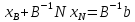


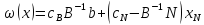
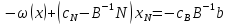
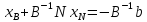
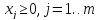
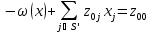 ,
,

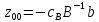
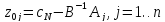 ,
,
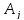 –столбец
матрицы А
–столбец
матрицы А
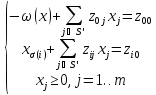
|
|
|
|
... |
|
|
|
|
|
… |
|
|
|
… |
|
… |
|
|
|
|
|
… |
|
|
|
… |
|
… |
|
|
|
|
|
… |
|
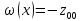
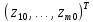 –базисное
решение
–базисное
решение
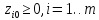 – допустимое базисное решение
– допустимое базисное решение
Опр.Симплекс-таблица
называется прямо допустимой, если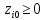 ,i=1..m
,i=1..m
Опр.Симплекс-таблица
называется двойственно допустимой,
если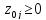 ,j=1..n
,j=1..n
Утв.Если ЗЛП разрешима, то существует прямо и двойственно допустимая симплекс-таблица
(ЗЛП
разрешима, если х не
 и ф-ия ограничена снизу)
и ф-ия ограничена снизу)
Утв.(достаточное условие оптимальности) если симплекс-таблица явл прямо и двойственно допустимой, то соответствующее базисное решение оптимальное.
Прямой симплекс-метод
0.построить нормальную симплекс-таблицу
1.если
с.-т. является двойственно допустимой
(т.е.
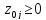 ,j=1..n), то
решение оптимальное и конец, иначе
переход к шагу2
,j=1..n), то
решение оптимальное и конец, иначе
переход к шагу2
2.определяем
ведущий столбец, т.е. находим такое j=s,
что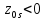 (если их несколько, то выбираем любой
из них)
(если их несколько, то выбираем любой
из них)
3.если
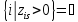 ,
то конец (ЗЛП решения не имеет), иначе
определяем ведущую строкуr:
,
то конец (ЗЛП решения не имеет), иначе
определяем ведущую строкуr: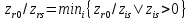 ,
,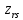 –ведущий
элемент
–ведущий
элемент
4.преобразуем
симплекс-таблицу с ведущим элементом
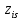 .
.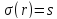 (Заменяем соответствующую базисную
переменную на небазисную) и переходим
к шагу1 (в результате с.-т. остается всегда
прямо допустимой)
(Заменяем соответствующую базисную
переменную на небазисную) и переходим
к шагу1 (в результате с.-т. остается всегда
прямо допустимой)
Метод искусственного базиса
Пусть
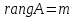 ,
все
,
все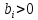
Введем
целевую ф-ию
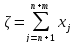 ,
(
,
( –искусственный
базис
–искусственный
базис
ограничения:
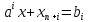

0.Формулировка задачи и построение симплекс-таблицы
1.Выполняем шаги 1-4 прямого симплекс-метода, находим оптимальное б.д.р
2.Если
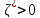 (для оптимального б.д.р.), то
(для оптимального б.д.р.), то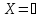 и конец (ЗЛП не имеет решения), иначе
и конец (ЗЛП не имеет решения), иначе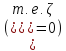 :
:
1)удаляем нулевую строку в симплекс-таблице
2)удаляем все столбцы искусственного базиса
3.если среди переменных б.д.р. останутся только переменные исходной задачи, то переходим к шагу7, иначе к шагу4
4.выбираем строчку r, соответствующую искусственной переменной
5.выбор
ведущего столбца: если
 ,
то выбираем
,
то выбираем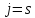 ,
осуществляем элементарное преобразование
базиса и переходим к шагу3, иначе к шагу6
,
осуществляем элементарное преобразование
базиса и переходим к шагу3, иначе к шагу6
6.удаляем
строку, для которой
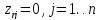 и переходим к шагу3
и переходим к шагу3
7.достраиваем нулевую строку в соответствии с исходной задачей, таким образом получаем прямо допустимую симплекс-таблицу исходной задачи
8.выполняем шаги 1-4 для полученной прямо допустимой симплекс-таблицы
3.Суть двойственных задач линейного программирования. Теоремы двойственности линейного программирования. Двойственный симплекс-метод.
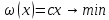
Ограничения:
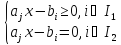 –сущ.ограничения
–сущ.ограничения
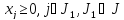 - неотрицательные переменные (остальные
- неотрицательные переменные (остальные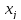 ,
,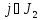 - свободные)
- свободные)
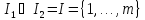 ,
,
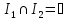

Двойственная задача ЛП
1.вводим
двойственные переменные
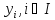
2.целевая
ф-ия
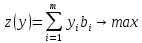
3.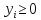 ,
,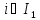
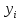 ,
,
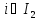 –свободные
–свободные
4.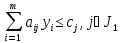
5.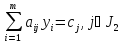
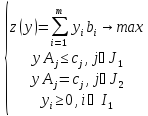 –двойственная
задача
–двойственная
задача
Теоремы двойственности
Свойства:
1.если
x и y явл. допустимыми решениями соотв.
прямой и двойственной ЗЛП, то всегда
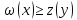
2.если x и y явл. допустимыми решениями
соотв. прямой и двойственной ЗЛП и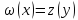 ,
то x и y являются оптимальными решениями
прямой и двойственной ЗЛП
,
то x и y являются оптимальными решениями
прямой и двойственной ЗЛП
Первая теорема двойственности
Прямая и двойственная к ней ЗЛП либо одновременно разрешимы, либо одновременно неразрешимы.
Причем в первом случае опт. знач. прямой и двойственной целевой ф-ии совпадают. Во втором случае по крайней мере одна из задач не разрешима из-за несовместности ограничений
Вторая теорема двойственности
Допустимы решения прямой и двойственной ЗЛП оптимально тогда и только тогда, когда:

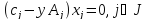
Двойственный симплекс-метод
0.Для прямой ЗЛП строим симплекс-таблицу, которая будет двойственно допустимой
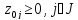
1. если построенная симплекс-таблица явл. прямо допустимой, то решение оптимальное и конец, иначе шаг2
2.выбираем
ведущую строку r: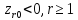
3.если
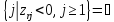 ,
то ЗЛП не разрешима и конец, иначе
выбираем ведущий столбец s:
,
то ЗЛП не разрешима и конец, иначе
выбираем ведущий столбец s:
4.преобразуем
симплекс-таблицу,
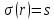 ,
переход к шагу1
,
переход к шагу1
4.Постановка задачи одномерной нелинейной оптимизации без ограничений и классификация методов ее решения. Основные методы решения задач одномерной безусловной оптимизации: деления интервала пополам, дихотомии, золотого сечения, чисел Фибоначчи, парабол.
Постановка
задачи: найти min f(x),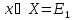 ,xконечном отрезке [a,b] –
интервал неопределенности
,xконечном отрезке [a,b] –
интервал неопределенности
Группы методов:
1) методы пассивного поиска (значения предыдущих итераций не используются)
2) методы активного поиска (инф-ия об экстремуме, кот. получили на предыдущих итерациях используется)
3) методы, основанные на аппроксимации целевой ф-ии (в основе аппроксимации – разложение в ряд Тейлора)
Алгоритм деления интервала пополам
1.задаем
значения a,b,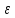
2.вычисляем
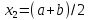 ,
,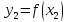
3.выч-м
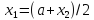 ,
,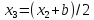 ,
, ,
,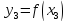
находим
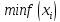 приi=1..3
приi=1..3
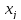 -точка,
в кот. мин. значение среди этих 3-х точек
-точка,
в кот. мин. значение среди этих 3-х точек
тогда
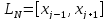 (
(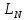 – конечный интервал неопределенности)
– конечный интервал неопределенности)
4.переобозначаем:
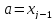 ,
,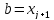 ,
,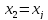 ,
,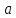 приi=0,
приi=0,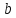 приi=4
приi=4
5.если
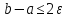 ,
то конец,
,
то конец,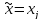 ,
иначе переход к шагу3
,
иначе переход к шагу3
Алгоритм, основанный на дихотомии
1.задаем
a,b,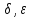 (
(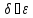 )
)
2.выч-м
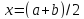
3.выч-м
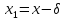 ,
,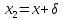 ,
,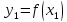 ,
,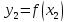
если
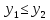 ,
то
,
то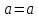 ,
,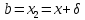
иначе
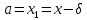 ,
,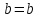
4.если
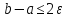 ,
то конец,
,
то конец,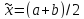 ,
,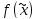 –min,
иначе переход к шагу2
–min,
иначе переход к шагу2
Метод золотого сечения
1.задаем a,b,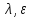 (
(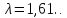 )
)
2.выч-м
 ,
,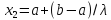 ,
, ,
,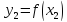
3.если
 ,
то
,
то ,
,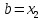 ,
,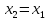 ,
,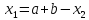 ,
,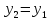 ,
,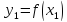
иначе
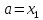 ,
,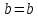 ,
,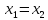 ,
,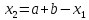 ,
,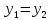 ,
,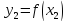
4.если
 ,
то конец и если
,
то конец и если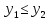 ,
то
,
то ,
иначе
,
иначе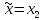 ,
,
иначе переход к шагу3
Метод Фибоначчи
N–число вычислений ф-ии задано(!)
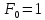 ,
,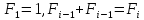
1.задаем a,b,N,k=1?k-номер итерации
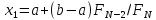 ,
,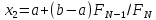 ,
,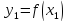 ,
,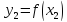
2.если
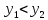 ,
то
,
то ,
,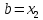 ,
,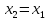 ,
,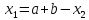 ,
,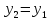 ,
,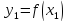
если
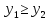 ,
то
,
то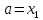 ,
,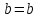 ,
, ,
,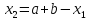 ,
,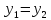 ,
,
3.если
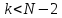 ,
то k=k+1 и повторяем шаг2, иначе конец и
если
,
то k=k+1 и повторяем шаг2, иначе конец и
если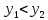 ,
то
,
то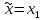 ,
иначе
,
иначе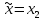
Метод парабол
1.задаем значения a,b,c,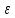 (a<c<b),
выч-мf(a),f(b),f(c)
и строим параболу
(a<c<b),
выч-мf(a),f(b),f(c)
и строим параболу
2. t–минимум параболы
если
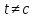 ,
тоx=t
,
тоx=t
если t=c, то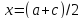
выч-м f(x)
3.переобозначаем: a)x<c
если f(x)<f(c), то a=a, c=x, b=c
если f(x)>f(c), тоa=x,c=c,b=b
если f(x)=f(c), то a=x, b=c, c=(x+c)/2
a)x>c
если f(x)<f(c), то a=c, c=x, b=b
если f(x)>f(c), то a=a, c=c, b=x
если f(x)=f(c), то a=c, b=x, c=(x+c)/2
4. если
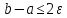 ,
то конец и
,
то конец и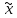 –одна
из 3-х точек (с мин. значением ф-ии), иначе
переход к шагу2
–одна
из 3-х точек (с мин. значением ф-ии), иначе
переход к шагу2