gos / шпоры / ОУ_мал

1.Структура систем управления.

Задача систем управления заключается в том, чтобы обеспечить заданные параметры развития тех или иных процессов.

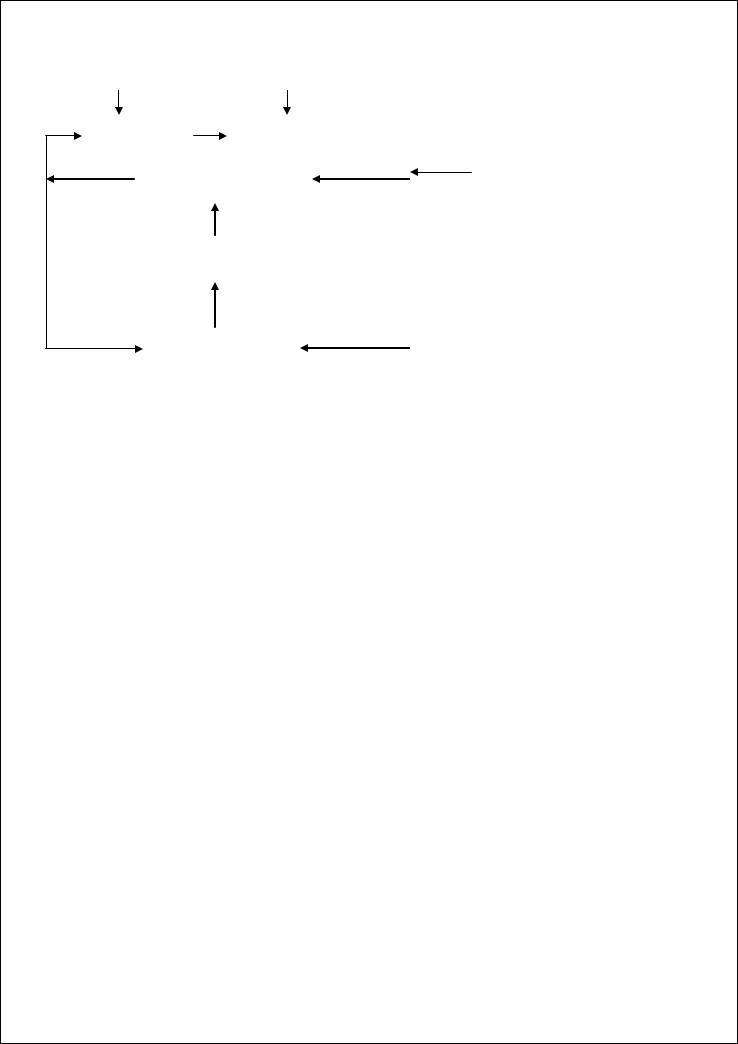
Современные системы управления заключают в себя следующие компоненты:

(t)

(t)

u(t)

Процесс (ОУ)

x(t)

Измерительная

yизм(t)

система

Внешняя СУ

Управляющее

устройство

x * (t), u * (t)

Блок формирования

эталонного процесса

ˆ

x, p

u(t)

yизм (t)

Информационный

блок

u(t) – функция управления

(t) – функция возмущения (возмущение) x(t) – состояние процесса

yизм – функция измерения системы (t) – функция шумов

Измерительная система – система датчиков, измеряющая параметры системы. Управляющее устройство – система типа вход-выход, где формируются законы управления.

x*,u* - эталонный процесс (пара функций, определяющих динамику изменения состояния и управления процессом )

Для работы блока формирования эталонного процесса необходима информация о действительном протекании физического процесса, т.е. функции u(t) и yизм- для информационного блока.

xˆ, p – система идентификации и оценки параметров процесса.

x – оценка состояния данного процесса p – оценка параметров системы

Существует также внешняя СУ, ее назначение – формирование внешних команд.

Если система не содержит внешнего управления, она наз. Автономной или самодостаточной.

1

2.Управляемость динамических систем.

Управляемость динамических систем является их важнейшей характеристикой и определяет условия, при которых задача управления имеет решение, то есть существует одна или несколько функций входа, называемых управлениями, под действием которых динамическая система может перейти в любое наперед заданное состояние.

Будем говорить, что динамическая система управляема относительно начального состояния x(t0 )
если существует управление u(t) из класса кусочно-непрерывных функций, которое переводит систему
	t0 0
из начального состояния в x(t f ) 0 за конечное время t f

Если динамическая система управляема относительно любого начального состояния, то данная система полностью управляема.

Найдем Математические условия управляемости линейных динамических систем с постоянными

параметрами.

Предположим, что начальное состояние удовлетворяет условию:

(t

xT

) 1,

некоторый n-мерный

0

Задано конечное состояние

) 0

под действием которого система

вектор. 0

x(t

f

и управление u ,

переходит в это состояние.

T

Исходная система x(t) Ax(t) Bu(t) и сопряженная система (t) A (t) , где примем (t0 ) .

Определим производную от скалярного произведения векторов состояния исходной и сопряженной систем:

d

dx(t)

d(t)

dx(t)

d(t)

(x(t), (t)) (

, (t))

(x(t),

) ( (t),

) (

, x(t))

dt

dt

dt

dt

dt

T

T

T

( (t), Ax(t) Bu(t))

( A

(t), x(t)) ( (t), Ax(t)) ( (t), Bu(t)) ( A

(t), x

(t))

(t)Bu(t)

Так как x, Ay		AT x, y , то 1 и 3 сокращаются.
Проинтегрируем это уравнение на интервале t0 , t f			T		T			t f	T
			: x	(t f ) (t f	) x	(t	0 ) (t0 )			(t)Bu(t)dt 1 (1),
								t0
	T
(t) e A		(t t0 ) (t) - вектор состояния сопряженной системы. Запишем систему из n соотношений
для функции		и ее (n-1) производной

Данную систему		можно записать в матрицу вида : T (t)G V T (t) (2) , G –матрица n x nm,
n-1		T	(t) - вектор 1x mn.
G=[B:AB:…:A	B]. V

Матрицу G часто называют матрицей управляемости.

Для управляемости системы необходимо и достаточно, чтобы ранг G был равен порядку системы. rang G=n

Док-во необходимости: u(t) - управление, под действием которого система переходит из начального

	) 0 , предположим, что rang G<n.
состояния в состояние x(t f

Согласно условию (1) (t) явл. однозначн. функцией, отличной от 0 для t t0 ,t f , поэтому если rang
G<n, матричное уравнение (2)		будет иметь ненулевое решение относительно ,		V (t) 0 . А если
V (t) 0 ,
	t f
T (t)B 0	T (t)Bu(t)dt 0		- противоречит условию 1 для управляемости исх.
	t0
системы необходимо rang G=n.
			2

Пусть rang G=n, тогда матричное уравнение 2 будет иметь ненулевое решение, если T (t)B 0 на

интервале управления t0 , t f	, это означает	t f
		T (t)BBT (t)dt 0 (3),		тогда решение u(t) BT (t) , u(t)

t0

– искомое	управление,	которое переводит	систему из состояния x(t0 ) в
константа,	которая	определяется	следующим	образом:

	) 0 .	-неизвестная
x(t f
t f

T (t)BBT (t)dt 1 ,

t0

t f
1/ T (t)BBT (t)dt
t0
			Таким образом определяется единственное решение задачи управления,

исходя из условия управляемости системы.

Для линейной системы с одним входом матрица управляемости является квадратной матрицей размера n x n и в этом случае система будет полостью управляема, если матрица управляемости не вырождена, т.е. определитель матрицы G отличен от 0. Det G

Свойство управляемости имеет важное значение, поскольку решение задачи синтеза оптимального управления существует только если система управляема.

3

3.Наблюдаемость динамических систем. Соотношение двойственности.

При синтезе оптимальных систем управление является функцией состояния системы, а не ее выхода.

Выход - координаты системы, которые поддаются измерению, следовательно, размерность вектора y

	будет меньше, чем размерность вектора x .
	При реализации оптимальных законов управления встает задача, как по вектору
			y оценить		x . Это
	задача наблюдения. Условие существования ее решения – наблюдаемость системы.
	Состояние xi (t0 ) наблюдаемо в момент времени t0 , если для заданного управления			t1 t0 , такое,
			u(t)
	что знание управления на интервале t0 ,t1 и выхода y t0 ,t1 достаточно для определения			xi (t0 ) .
	Если каждое состояние x(t0 ) наблюдаемо при t0	, то говорят, что система наблюдаема в t0 .
		любой момент времени t0 , то говорят, что
	Если каждое состояние x(t0 ) наблюдаемо в				система

(полностью) наблюдаема.

Понятия управляемости и наблюдаемости являются внутренними свойствами системы, то есть они сохраняются при всех эквивалентных преобразованиях системы.

,t

(1)

x(t)

A(t)x(t) b(t)u(t) t

0

1

y(t) c(t)x(t)

u(t), y(t) – функции входа и наблюдаемого выхода системы. А,В,С – известные матрицы.

Наряду с исходной системой рассмотрим сопряженную к ней систему:

T

(t)S (t) C

T

(t)v(t)

(2)

S (t) A

Определим производную от векторов состояния исходной и сопряженной системы.

d

dS

dx

T

T

(S (t), x(t))

(

, x)

(S,

)

( A (t)S (t) C

(t)v(t), x(t)) (S (t), A(t)x(t) Bu(t))

dt

dt

dt

T

(C

T

( A (t)S (t), x(t))

(t)v(t), x(t))

(S (t), A(t)x(t)) (S (t), Bu(t))

v

T

T

(t)C(t)x(t)

S

(t)Bu(t)

Проинтегрируем это выражение

T

T

t1

T

t1

T

S

(t1 )x(t1 ) S

(t0 )x(t0 )

v

(t)C(t)x(t)dt

S

(t)B(t)u(t)dt

t0

t0

Принимаем S(t1) 0 и учитывая (1), получим:

T

t1

T

t1 T

S

(t0 )x(t0 ) v

(t) y(t)dt

S

(t)B(t)u(t)dt

(3)

t

t

Если известно

0

0

v(t) , то данное выражение можно считать операцией оценки, которое позволяет оценить

x(t0 ) , если известны y(t), u(t) (векторы).

Вектор S (t0 ) выбирается в зависимости от того, какая из переменных состояния оценивается.

	Если нужно оценить xi (t0 ) , то i-я компонента S (t0 ) принимается = 1, остальные = 0.
		0
	Si	(t0 ) 1		i
		0		не плюс i, а на i-ом месте
	Если сопряженная система управляема, то должна существовать функция входа
					v(t) под действием

которой данная система переходит из исходного состояния Si (t0 ) в 0 за время t1 t0 .

4

	(t) - функция входа, которая решает данную задачу, тогда состояние xi (t0 ) определяется из
Пусть vi
соотношения (3).
	t1	T		t1 T
xi (t) v			(t) y(t)dt S		(t)B(t)u(t)dt	(4)
	t0			t0

Следовательно, анализ наблюдаемости динамических систем свелся к задаче управляемости сопряженной системы.

Данная взаимосвязь между управляемостью и наблюдаемостью линейных динамических систем называется соотношением двойственности.

Соотношение двойственности указывает на то, что исходная система (1) наблюдаема, если сопряженная к ней система (2) управляема.

Управляемость сопряженной системы имеет место, если выполняется следующее условие:

t1

det ФT (t,t0 )CT (t)C(t)Ф(t,t0 )dt 0

t0

t1 t0

5

4.Оценка вектора состояния линейной динамической системы. Наблюдатель Люенбергера.

Решение задачи ОУ приводит к закону управления, который является функцией переменных состояния, следовательно, при решении этих задач полагается, что вектор состояния полностью известен, однако в реальных системах это условие как правило не выполняется.

Чаще всего приходится сталкиваться с ситуацией, когда измерению поддаются сигналы, образующие вектор измерения y(t), составляющие которого являются известными функциями состояния системы. Устройство, восстанавливающее вектор состояния по измеряемым координатам называется наблюдателем.

dxˆ

Система n-го порядка:

F (t)xˆ(t)

G(t) y(t) H (t)u(t) (1) xˆ - вектор оценки

dt

Состояния

системы

является

наблюдателем

полного

порядка для системы вида

(2)

dx(t)

A(t)x(t)

b(t)u(t)

(2)

dt

y(t) c(t)x(t)

При xˆ(t

t t0

)

) x(t

имеем xˆ(t) x(t) (совпадение вектора оценки и состояния) для всех u (t ) ;

0

0

Будем рассматривать наблюдатель, у которого F, G и H определяются следующим образом:

F (t) A(t) kH (t)c(t)

(3) kH - матрица коэффициентов усиления наблюдателя (n x m).

G(t) kH (t)

B(t)

H (t)

Подставим

(3)

в

(1):

dxˆ

(4)

[ A(t) k H (t)c(t)]xˆ

(t) k H (t) y(t) B(t)u(t)

dt

dxˆ

A(t)xˆ(t) B(t)u(t) kH (t)[ y(t) yˆ(t)]

(5)

dt

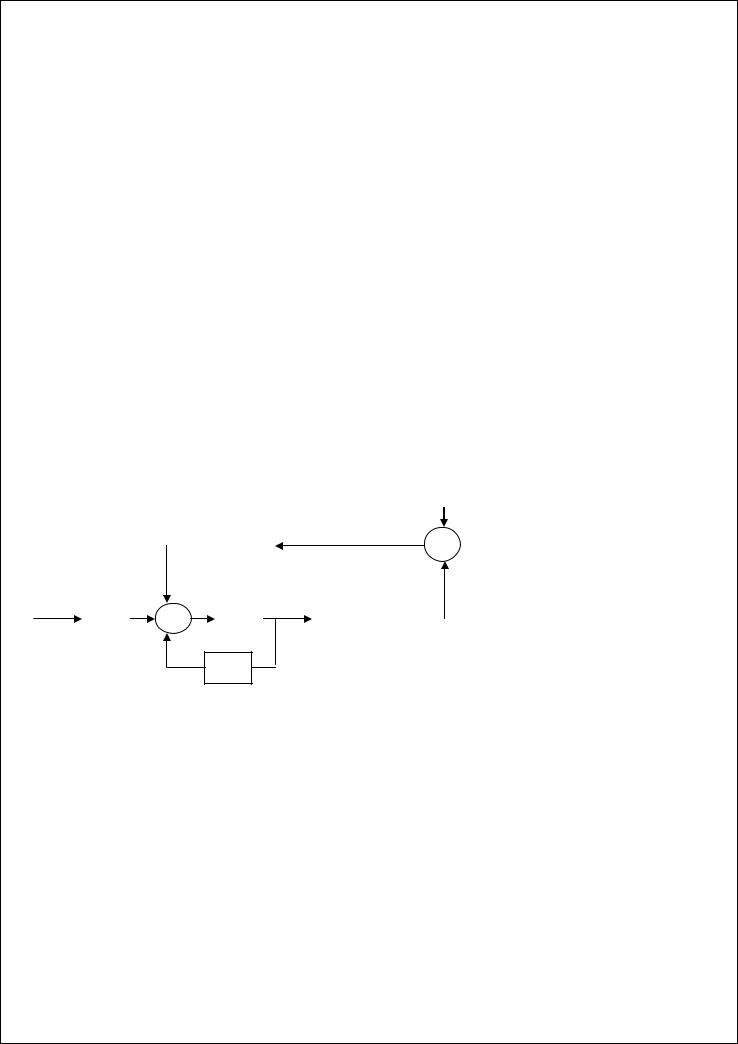
yˆ(t) c(t)xˆ(t) оценка вектора наблюд.

Структурная схема наблюдателя:										y(t)
								+
				KH(t)
										(–)
										y(t)
u(t)	B(t)					xˆ	(t)			ˆ
		+						C(t)

A(t)

Наблюдательэто устройство, позволяющее по управлению и измеряемым координатам оценить вектор состояния системы.

Докажем, что система вида (5) есть система для оценки вектора состояния.

Пусть S(t)- решения сопряженного уравнения, удовлетворяющего краевым условиям, при которых

T					t1	T		t1	T
соотношение S	(t	0 )x(t0 ) v					(t) y(t)dt S			(t)B(t)u(t)dt является операцией
					t0			t0
			0
оценки. ( S (t1 ) 0; S (t0 ) Si			1		i )
			0

Из теории решения 2-х точеных задач известно, что v(t) является функцией состояния сопряженной системы.

6

T

v(t) kH

(t)S(t)

T

(t) C

T

T

T

(6)

S(t) ( A

(t)kH

(t))S(t) или S(t) ( A(t) kH

(t)C(t)) S(t)

Система (6) является сопряженной для системы (4)

(t)) (S (t), dxˆ(t) )

d (S (t), xˆ(t)) ( dS (t) , xˆ

dt

dt

dt

(( A kH C)T S (t), xˆ(t))

(S (t), (( A kH C) xˆ

(t)) Bu (t) kH

(S (t), ( A kH C) xˆ(t)) (S (t), ( A kH C) xˆ

(t)) (S (t), Bu (t))

(S (t), Bu (t))

(S (t), kH y(t))

y(t))

(S (t), kH y(t))

t1

t1

проинтегрируем S (t1 )xˆ

(t1 ) S (t0 )xˆ(t0 )

(S (t), B(t)u(t)dt)

(S (t), kH y(t))dt

t0

t0

T

(S(t), kH y(t))dt (kH

S(t), y(t))

(v(t), y(t))

T

t1 T

t1

T

S

(t0 )xˆ(t0 ) (S

(t), B(t)u(t)dt) v

(t) y(t)dt

то есть вектор оценки совпадает с вектором состояния в

t0

t0

момент t0

xˆ(t0 ) x(t0 )

Следовательно, система вида (4, 5) есть система для оценки состояния.

Введем в рассмотрение вектор оценки x(t) x(t) xˆ(t) (вектор ошибки оценки)

Ошибка оценки удовлетворяет следующему диф.уравнению:

d x(t)

[ A(t)

kH (t)c(t)] x(t)

(7)

dt

( A kH C )(t t0 )

Решение этого уравнения имеет вид: x(t) e

(8)

Если вектор оценки совпадает с вектором состояния в момент t0 , то вектор ошибки x(t) 0 для t t0 .

xˆ(t0 ) , поэтому матрицу kH (t)

В реальных системах из-за действия возмущений и шумов x(t0 )

выбирают таким образом, чтобы ошибка наблюдения 0 при t . lim x(t) 0

т.е. система вида (7)

t

должна быть асимптотически устойчивой.

Для системы с постоянными параметрами асимптотическая устойчивость наблюдателя определяется собственными значениями матрицы A kH c . Назовем их полюсами наблюдателя. Для устойчивости

наблюдателя необходимо и достаточно, чтобы полюса наблюдателя находились в левой полуплоскости. Наблюдатель рассматриваемого вида для системы с постоянными параметрами называется наблюдателем Люенбергера.

Для быстрой сходимости ошибки к 0 необходимо выбрать kH таким образом, чтобы полюса

наблюдателя были удалены как можно больше влево от мнимой оси корневой плоскости. Решение уравнений (7) помимо вида (8) может быть представлено следующим образом:

						P, P		1
x(t) Pe (t t0 ) P					1 x(t0 )			- матрицы правого и левого собственных векторов.
			1	(t t0 )
e (t t0 )		e					0
									1... n - отрицательные полюса наблюдателя.
				0		e	n (t t0 )

Чем больше по модулю будут полюса наблюдателя, тем ближе к нулевой будет матрица e (t t0 ) и

меньше . Однако значительное удаление от мнимой оси влево в большинстве случаев может быть

x(t)

достигнуто путем выбора больших значений коэффициентов матрицы усиления, что, в свою очередь, делает наблюдатель весьма чувствительным к шумам измерения. Задача определения матрицы

7

коэффициентов усиления kH , обеспечивающей наилучшие характеристики процесса восстановления в условиях действия шумов называется задачей оптимальной фильтрации.

8

5.Теорема Куна-Таккера, следствие из нее.

Теорема Куна-Таккера. Пусть		g					* - точка
	H (u) и		(u) дифференцируемы по u			в области U и u
		i
				0.	Тогда существуют такие неотрицательные числа i
максимума для H (u) , при ограничении		gi (u)

0, что выполняется следующее равенство:

		r			* ) 0
u H (u		* ) i u gi (u

i 1

Причем	=0 для всех i для которых	g		* ) 0 .(
			(u
i		i

то есть для неэффективных ограничений.) Причем i >0 для всех i

для которых g

(u* ) 0 .( то есть для эффективных ограничений.)

i

Доказательство:

*

точки максимума для

Пусть u

H (u) .

Надо рассмотреть два случая:

*

— внутренняя точка. Тогда

1. Случай внутренней точки. Пусть u

положим все i

= 0, т.к. ограничения будут

неэфективны.

производная ф-ии в точке экстремума

*

опорную

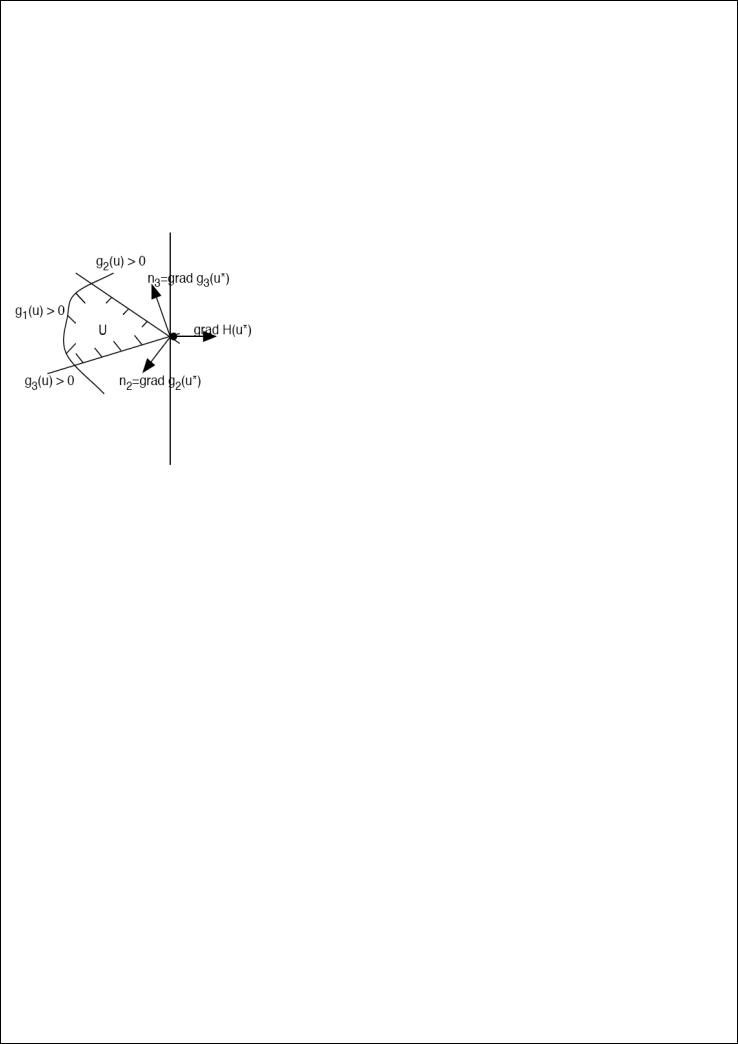
2. и* — граничная точка. Проведем через точку u

гиперплоскость Г, и направим все нормали по градиенту функции.

Можно записать следующее соотношение:

u H (u)

2 g2 (u) 3

g3 (u) u H (u) 2 g2 (u) 3

g3 (u) 0

1 = 0, так как ограничение g1 неэффективно (то есть данная точка этому ограничению не

принадлежит).

Следствие 1. Если

* — точка, где

достигает своего

H (u)

дифференцируема по u в области U, а u

H (u)

максимума, то для всех направлений, допустимых в этой точке выполняется следующее неравенство

				0 .
T H (u)d			*
	u	u
								0
1.		*		- внутренняя точка, то		u	H (u* )
	Если u
2.		*		— граничная точка, то выполняется условие теоремы Куна-Таккера.
	Если u

Следствие 2. Если функции H вогнута относительно управления, то необходимое условие оптимальности оказывается и достаточным. Найденное в этом случае управление оказывается оптимальным в глобальном смысле, т.к. экстремум такой функции — максимум, причём единственный.

9

6.Теорема о числе переключений.

Если

1.Задана система обыкновенных дифференциальных уравнений вида

2.Матрице А имеет все вещественные собственные значения

3.На управление наложены следующие ограничения вида u j u j max , j=1,..,m

то число переключений функции оптимального по быстродействию управления не превышает n-1, где n

– порядок исходной системы.

Доказательство: Запишем закон движения объекта в следующем виде

x(t)

	m
Ax(t) b j u j		(t)

j 1

Оптимальное управление Куна-Таккера определяется следующим образом:

u*j (t) u j max * sign( T (t)b j )

В этом выражении функция ψ(t) может быть определена из следующего диф.уравнения

(t)

H ( , x, u, t)

dx

H –функция Гамильтона

H T (t) Ax(t)

m

T b j u j (t)

j 1

	H
Т.е. нам нужно найти производную по х:				( T Ax) AT
	dx		dx

Решение имеет вид 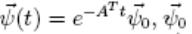— начальное значение в момент времени t0 = 0. Один из

способов задания 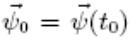— нормаль к опорной гиперплоскости в точке х(t0) Перепишем выражение для оптимального управления с учётом ψ(t):

*	(t) u j max	* sign(e	AT t	,bj	) u j max		, e	At	,bj	)
u j			0			* sign( 0

Представим eAt в виде спектрального разложения eAt = ρeλtρ−1, где р, ρ−1 — матрицы правых и левых собственных векторов.

Если воспользуемся матричным свойством C = AB => С −1 = B−1A−1, получим

*
Значит, оптимальное управление u j		будет определятся как
						n
			, e t 1bj		u j max	* sign( i e it )
u*j (t) u j max * sign(	0			)

i 1

j — некоторые коэффициенты, которые опредляются матрицами ρ и ρ−1 и векторами bj и ψ0 и не зависят от времени. Тогда моменты переключения управления — это моменты, когда выражения под

n

знаком sign’ма равно 0. Число переключений определяется корнями этого выражения: i e it =0.

i 1

Рассмотрим случай, когда n = 2. При суммировании экспонент будет либо одно пересечение c осью времени, либо не будет ни одного. По индукции можно доказать, что сумма n экспонент будет иметь не более (n − 1) пересечений с осью времени.

Замечание. Данная теорема верна только в случае действительных корней матрицы A. При комплексных корнях появится функция sin, и следовательно, пересечений будет бесконечно много.

Таким образом, мы нашли оптимальное управление как функцию ψ(t)

10