1. Уравнения динамики и статики объектов управления.

Различные по физической природе объекты управления могут описываться однотипными математическими зависимостями. Построение любой системы управления начинается с изучения объекта управления и составления его математического описания, которое может быть получено экспериментальным, аналитическим или комбинированным путем.

{В первом случае уравнения объекта получают путем постановки специальных экспериментов на объекте (метод активного эксперимента) либо статистической обработкой результатов длительной регистрации координат объекта в условиях его нормальной эксплуатации (метод пассивного эксперимента).

При аналитическом описании уравнения объекта получают на основании физико-химических закономерностей протекающих в нем процессов.

Комбинированный путь получения математического описания объектов подразумевает обычно составление уравнений аналитическим путем с последующим уточнением коэффициентов этих уравнений экспериментальным методом.}

Уравнения объектов автоматического регулирования в зависимости от описываемого ими режима работы подразделяютсяна уравнения статики и динамики.

Уравнения динамикиописывают неустановившийся или переходный режим в объекте. Выходная координата объекта при этом является функцией времени и в общем виде уравнение динамики будет дифференциальным уравнением, содержащим производные по времени.

Объекты управления называются линейными, если они подчиняются принципу суперпозиции, который заключается в том, что реакция объекта на сумму входных сигналов равна сумме реакций на каждый из сигналов в отдельности. Линейные объекты описываются линейными дифференциальными уравнениями, то есть уравнениями, в которых искомая функция и ее производные содержатся в первой степени.

Уравнение динамики (представляет из себя ОДУ):

a_n*(dⁿx(t)/dtⁿ)+…+ a₁*(dx(t)/dt)+ a₀*x(t)= b₀*g(t)+…+ b_m*(d^mg(t)/dt^m).

Начальные условия: x(0),…,x^(n-1)(0).

– условие физической реализуемости.

Уравнения статикиописывают установившийся режим, при котором все координаты объекта остаются неизменными во времени, то есть объект находится в состоянии равновесия. Они представляют собой алгебраические или дифференциальные уравнения, содержащие производные по какому-либо параметру, кроме времени. Существенной особенностью уравнений статики является неизменность координат объекта во времени.g(t)=const=g₀,x(t)=const=x_0.

Если g(t)=const=g₀, то x(t)=const=x₀. Тогда уравнение динамики преобразуется в уравнение статики:

a₀*x₀=b₀*g₀.

2. Передаточные функции объектов и устройств управления.

Классический подход предполагает переход от временной области в область изображений.

Преобразование Лапласа.

L[x(t)]=X(S) – линейный оператор.t– время,S– переменная ЛапласаS=σ+jω.

X(S)= ∫x(t)e^-stdt(интеграл берётся от 0 до ∞).

x(t)=L^-1[X(S)]=1/2πj*

Задача Коши.

Линеаризация возможна при малых возмущениях.

L[x¹(t)]=S*X(S)-X(0⁺)

…

L[xⁿ(t)]=Sⁿ*X(S)-S^n-1*X(0⁺)- …-X^n-1(0⁺)

Теорема свертки:

Применим преобразование Лапласа к ОДУ, описывающее ЛДС:

a_nSⁿX(S)+a_n-1S^n-1X(S)+…+a₁SX(S)+a₀X(S)–M_н.у.(S)=

=b_mS^mG(S)+b_m-1S^m-1G(S)+…+ b₁SG(S)+ b₀G(S)

Начальные условия (nштук):x(0⁺),..,x^(n-1)(0⁺)

Положим начальные условия нулевыми.

X(S)[a_nSⁿ+…+a₀]=G(S)[b_mS^m+..+b₀]+M_н.у.(S)

X(S) =G(S)W(S)

W(S)=X(S)/G(S) – передаточная функция ЛДС – это отношение изображений выходного сигнала к входному при нулевых начальных условиях.

D(p) совпадает сD(S)

M(p) совпадает сM(S)

Передаточная функция может быть детализирована по 2-м направлениям:

1.типовые звенья

2.представление в виде нулей и полюсов

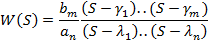
g(t)

3. Основные характеристики типовых звеньев во временной и частотной областях.

3типа входных воздействий:

- ступенчатое;

- импульсное;

- гармоническое.

Переходная функция.

Реакция системы на ступенчатое входное воздействие называется переходной функцией (h(t)).

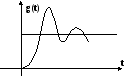
(преобразование Лапласа)

- единичное ступенчатое воздействие

Весовая функция ЛДС.

Реакция системы на импульсное входное воздействие называется весовой функцией.

g(t) = 1*(t-0)

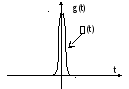
амплитуда бесконечна.

L[(t)] = 1

G(s) = 1

w(t) – весовая функция ЛДС (импульсная переходная функция).

– реакция имп. системы при нулевых начальных условиях.

Реакция на гармоническое воздействие

На вход подается гармоническое воздействие: g(t)=g₀sinωt,ω=const

Амплитудно-фазовая характеристика.

На вход подается гармоническое воздействие: g(t)=g₀sinωt,ω=const

0 < +

P() – вещественная ЧХ,Q() – мнимая ЧХ.

Амплитудно-фазовая ЧХ:

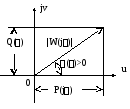
Типичный случай АФЧХ:

;

3. Логарифмические частотные характеристики типовых звеньев, минимально-фазовые и неминимально-фазовые типовые звенья.

логарифмическая амплитудно-частотная хар-ка, дБ(децибел)

i – полюсы 1,..n -нули 1,..m m<=n

Наиболее часто встречающиеся звенья со множителем, типовые звенья:

Типовые звенья делятся на минимально-фазовые(поведения амплитуды и фазы строго согласовано, есть закономерность) и неминимально-фазовые(несвязанны между собой, нет между ними закономерности).

Во всех графиках перегибы в точке 1/Т !

I. Минимально-фазовые звенья: (график: L(w) по вертикали и w,c^-1 по горизонтали)

1) Усилительное звено

W(s)=k k>0,коэффициент передачи. Высота линии на рисунке 20lgk

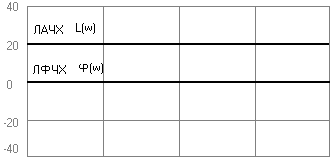
2) Интегрирующее звено {}

Наклон -20дБ/декада

3) Апериодическое звено

погрешность 3дБ

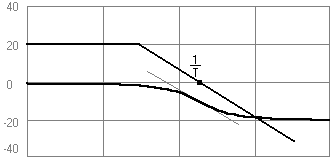
4) Колебательное звено

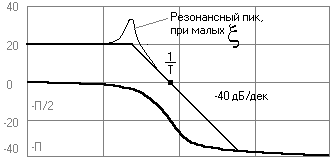
Если 0,4≤ζ≤0,7 погрешность =+/-3дБ при ζ=1 колебательное звено исчезает и появляется 2 апериодических

5) Дифференцирующее звено 1-го порядка

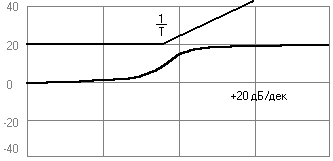
6) Дифференцирующее звено 2-го порядка

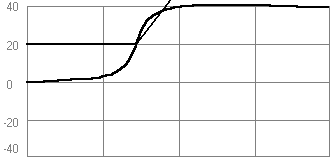
{7) Звено «чистого» дифференцирования (дифференцирующее звено)

W(s)=ks}

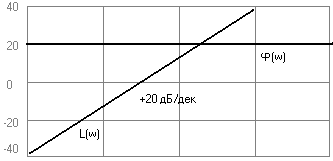
{Свойство минимально-фазовых звеньев +-n->+-(pi/2)*n}

II. Неминимально-фазовые звенья:

1) Неустойчивое апериодическое звено

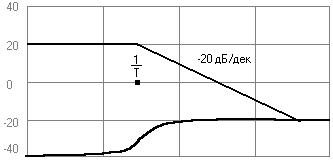
2) Неустойчивое колебательное звено

(присутствует как минимум один минус)

3. Дифференцирующее звено 1-го порядка

W(s)=k(1-τs)

4) Дифференцирующее звено 2-го порядка

5) Звено «чистого» запаздывания

W(S)=e^-τs