gos / шпоры / ЦОС_мал

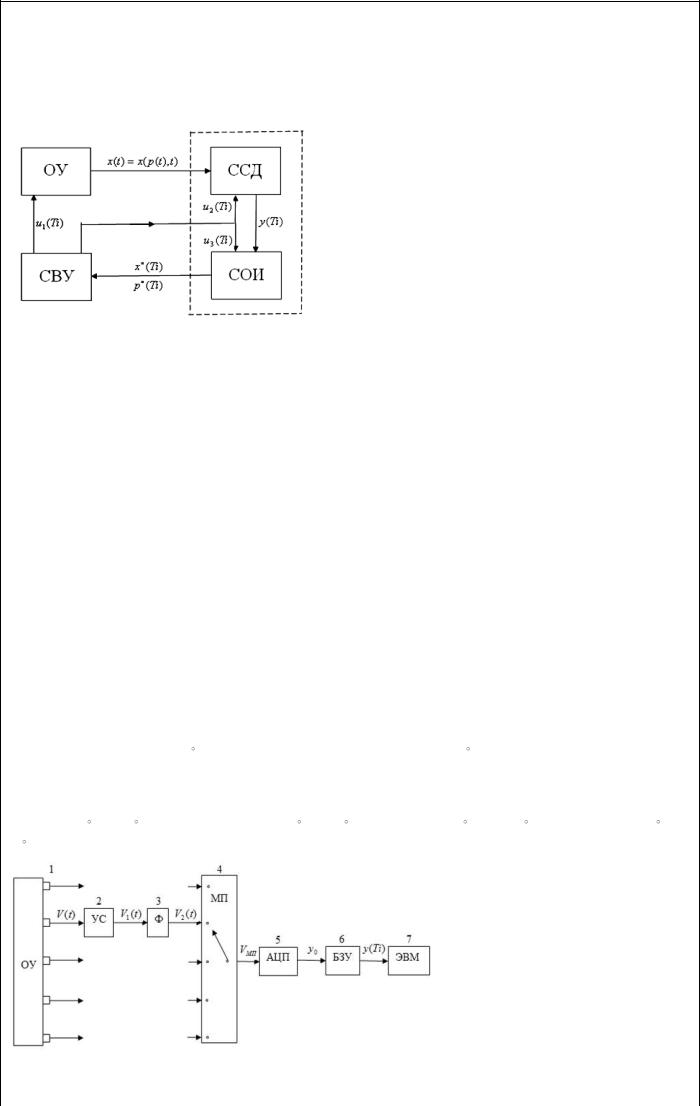
1. Структура систем ЦОС. Структура систем сбора данных

Структура цифровых информационно-управляющих систем (ИУС) для общего случая представлена на блок-схеме

Типовая цифровая ИУС состоит из четырёх составляющих систем: 1) ОУ – объекта управления; 2) ССД – системы сбора данных; 3) СОИ – системы обработки информации; 4) СВУ – системы выработки управления. системы ОУ,

ССД, СОИ и СВУ-прямоугольники; стрелки-направления движения входной и выходной информации. Система ЦОС, являющаяся частью ИУС, состоит из ССД и СОИ и помещена в пунктирный прямоугольник

ОУ – объект управления – характеризуется векторами входных управляющих переменных u1(Ti) (u1(t)) и векторами выходных переменных, которые в ряде случаев определяются как векторы фазовых координат x(t) x( p(t), t), p(t) –

векторные параметрические функции.

. В простейшем случае для статических ОУ связь между входными и выходными переменными определяется модельными нелинейными функциями от нескольких переменных, которые можно представить в скалярном или векторном виде:

	x1(t) f1( p1(t),..., pq (t), u11(t),..., u1m (t)),
. . .	(1.1.1)
x1(t) f1( p1(t),..., pq (t), u11(t),..., u1m (t)),
x(t) f (x(t), p(t), u1(t)) .	(1.1.2)

Связь между векторами управляющих переменных и векторами фазовых координат для динамических ОУ определяется системами модельных дифференциальных уравнений. Для динамических ОУ с сосредоточенными параметрами модельные дифференциальные уравнения в векторном виде представляются следующим образом:

dxdt f (x(t), p(t), u1(t)) .

.

{Необходимо отметить отличия параметрических функций p(t) и управляющих переменных u1(Ti) . Управления u1 (Ti) являются полностью известными; параметрические функции p(t) – некоторые неизвестные функции, относительно которых могут быть сведения только об их самых общих характеристиках.}

ССД – система сбора данных – обеспечивает промежуточное накопление и предварительную цифровую обработку многоканальной информации об объекте управления. На вход системы ССД поступает вектор фазовых координат x(t) x( p(t), t) и вектор управления u2 (Ti) , реализующий настройку ССД. Выходом ССД являются векторы наблюдений y(Ti) фазовых координат, связанные с фазовыми координатами x(Ti) и помеховыми возмущениями w(Ti) , которые обусловливают погрешности в наблюдениях. Наблюдения описываются следующей модельной

зависимостью: y(Ti) h(x(Ti), w(Ti), u2 (Ti)) ,		(1.1.3)
где вид модельной функции наблюдения h( , , ) определяется конструкцией ССД.
СОИ – система обработки информации – обеспечивает по входной информации-наблюдениям от ССД			y(Ti) и
вектору управления u3 (Ti),	который предназначен для настройки алгоритмов СОИ, решение задачи вычисления
оценок фазовых координат	x (Ti) и оценок параметрических функции p (Ti) , которая, по-существу,		является

центральной для ЦОС.

СВУ – система выработки управлений – осуществляет формирование необходимых управляющих воздействий

u1(Ti) для ОУ, u2 (Ti) для ССД и u3 (Ti) для СОИ по информации от СОИ.				В общем виде можно записать:
u1(Ti) u1(x (Ti), p (Ti)),	u2 (Ti)	u2 (x (Ti),	p (Ti)), u2 (Ti) u2 (x (Ti),	p (Ti)),		u3 (Ti) u3 (x (Ti),
p (Ti)) .
			Структура ССД существенным образом
			определяет		возможности		проведения
			ЦОС. ССД состоит из системы датчиков,
			усилителей,		противомаскировочных
			фильтров, электронных коммутаторов,
			аналого-цифровых преобразователей и
			устройств		буферной		памяти.
			упрощённой конструкции ССД, цифрами
			отмечены основные элементы системы.

ССД состоит из системы датчиков,

1

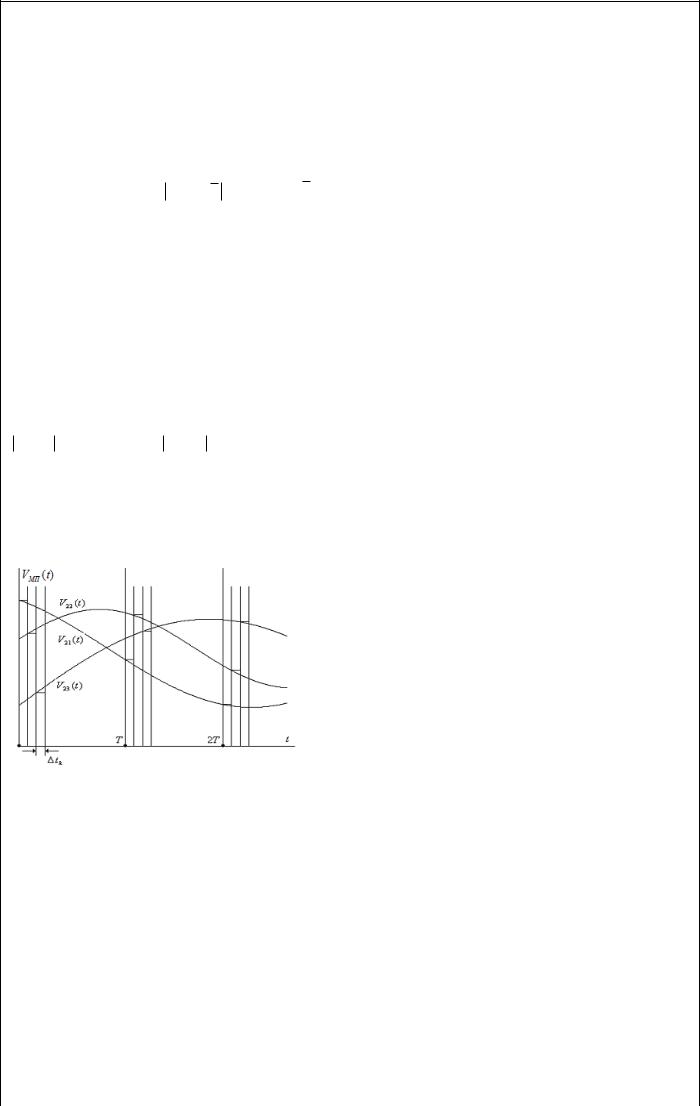
усилителей, противомаскировочных фильтров, электронных коммутаторов, аналого-цифровых преобразователей и устройств буферной памяти.

Датчики назначение которых состоит в преобразовании фазовых координат объекта x(t) в систему

электрических сигналов – выходные напряжения V (t) , в которых содержится информация о параметрах объекта.

Каждому датчику ставится в соответствие функция преобразования, которая связывает значение величины x(t) со значением напряжения V (t).

Усилители назначение данных усилителей cостоит в обеспечении усиления входных сигналов до стандартного значения: K1V (t) V1(t) , V1(t) V1 , чаще всего V1 1 В. Частотные характеристики передаточной функции для УС должны быть подобраны таким образом, чтобы для входного сигнала V (t) в заданном частотном диапазоне амплитудные и фазовые искажения были незначительными.

Противомаскировочные фильтры На вход аналогового противомаскировочного фильтра подаётся сигнал V1(t),

выходной сигнал фильтра обозначается в виде V2 (t). Низкочастотные аналоговые фильтры (непропускающие высокие частоты) с передаточными функциями ( j ) обеспечивают устранение высокочастотных составляющих в выходном сигнале V2 (t). Как правило, для противомаскировочных фильтров их АЧХ в точке среза

с должны иметь большую крутизну. Вследствие чего в рабочей полосе частот (0, c ) коэффициент усиления фильтра должен быть примерно равен 1, в высокочастотной области ( c , ) коэффициент усиления фильтра должен быть близок к нулю:

( j ) 1 , 0 c ; ( j ) 0 , c .Частота среза c аналогового фильтра обычно регулируется в зависимости от полосы исходного сигнала (его частотных свойств) и заданной частоты дискретизации.

Электронные коммутаторы Электронный коммутатор (мультиплексор) реализует переключение измерительных каналов с частотой дискретизации fd 1/ T , T – интервал временной дискретизации Следует отметить, что использование в ССД электронного коммутатора не является обязательным; его применение диктуется

в ряде случаев требованием уменьшения аппаратурных затрат для снижения числа микросхем АЦП

для трёх

информационных входных каналов, на которые подаются

напряжения V21(t), V22 (t), V23 (t) , приведён на рис. 1.3.7.

С временным шагом дискретизации T происходит

запоминание

на

время

t k

(время

коммутации)

соответствующего кусочно-постоянного напряжения, которое

предназначено для подачи в устройство дискретизации. Для

работы электронного коммутатора должно выполняться

соотношение n tк T.

АЦП

Аналого-цифровые

преобразователи

(АЦП)

осуществляют

преобразование последовательности

кусочно-постоянных напряжений от мультиплексора

VМП VМП (t)

в последовательность цифровых кодов

у0 y0 (Ti) . Следует отметить существенные параметры

АЦП для формирования систем ЦОС: 1) tАЦП – время преобразования АЦП аналогового напряжения

V2i (t) в

цифровой код; очевидно, должно выполняться неравенство tАЦП tk ;

2) LA – число разрядов цифрового кода с

выхода АЦП (не считая знака); 3) VАЦП – рабочий диапазон АЦП по входному напряжению; этот параметр

y0 (Ti)

устанавливается стандартным рядом значений – чаще всего V

АЦП 1 и 5 В. Последовательность

с выхода

АЦП является дискретизованной по времени и по уровню.

Ус-во буферной памяти На вход буферного запоминающего устройства (БЗУ) поступают данные от АЦП. БЗУ обеспечивает промежуточное хранение массивов дискретизованных данных. Для БЗУ следует отметить параметры,

существенные при реализации сбора данных: 1) tБЗУ – время ввода одного кода от АЦП в БЗУ; tБЗУ T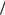n; 2) объем памяти БЗУ – VБЗУ в Кб (Мб), где б – байт. При формировании конкретной системы сбора данных необходим учёт типа памяти БЗУ.

2

2. Аппроксимация наблюдений для линейных моделей, действительный и комплексный случай.

наблюдаемый

сигнал y(t)

связан с исходным сигналом

x(t) x( p(t), t) и

случайным

помеховым

возмущением w(t) через модельную функцию наблюдения h( , )

известного вида

y(t) h(x(t), w(t)) h(x( p(t), t), w(t)).

Действительный случай:

есть

наблюдения

y(i) y(Ti)

на

конечном

временном

интервале

для

m

i 0,1,..., N 1.

Представим линейную по

параметрам модельную функцию:

yM (c,

Ti) cr r (Ti),

r 1

i 0,1,..., N 1.

зависящая

от

вектора

параметров

cT (c ,...,

c

)

,

T (Ti) ( (Ti),..., (Ti))

в

1

m

1

m

скалярном виде: yM (c, Ti) cT (Ti).

функционал

S(c, y),

мера

близости

модели

и

наблюдений,

определяется

разностями

N 1

N 1

y(c, Ti) y(i) cT (Ti).

S(c, y) =

y2 (c, Ti) ( y(i) cT (Ti))2.

линейности S имеет

i 0

i 0

(из-за

квадратич. Форму)

векторно-матричные переменные:

y(0)

c1

1(T 0),

2 (T 0),

...

m (T 0)

Y

y(1)

, c

c2

, X

1(T 1),

2 (T 1),

...

m (T 1)

,

.

.

.

.

...

.

y(N 1)

cm

1(T (N 1)),

2 (T (N 1)), ...

m (T (N 1))

где Y – вектор наблюдений размерности (N,1);

c – вектор параметров модели размерности (m, 1);

X –

матрица плана сигнала размерности (N, m).

Нетрудно видеть, что разность для наблюдений и модели

может быть сформирована в векторном виде

Y (c) Y Xc .

(2.4.5)

На основе введённых векторов и матриц функционал S(c, Y )

записывается как скалярное произведение и

представляет собой квадратичную форму

S(c, Y ) Y T (c) Y (c) (Y Xc)T (Y Xc)

(2.4.6)

Y T Y Y T Xc cT X T Y cT X T Xc.

С учётом того, что имеет место равенство YT Xc cT X TY ,

можно записать

S(c, Y ) YTY 2cT X TY cT X T Xc.

=0 ;

;

минимальное значение этой квадратичной формы достигается при

c

(X T X ) 1 X T Y.

(2.4.7)

Представим в виде системы линейных уравнений (в лекциях D=A, d=a)

X T X c X T Y.

Введём обозначения D X T X , b X T Y. Матрица D имеет размерность (m, m); элементы этой матрицы симметричны относительно главной диагонали и определяются как скалярные произведения базисных функций

N 1
drs r (Ti) s (Ti),	r, s 1,..., m.
i 0

Элементы вектора b X T Y размерности (m,1) – коэффициенты Фурье, вычисляются как взвешенные

суммы наблюдений

N 1

br r (Ti) y(i) , r 1,..., m.

i 0

Нахождение оптимального вектора параметров c сводится к решению линейной системы уравнений

Dc b.

3

Комплексный случай: Рассмотрим решение задачи оценивания параметров линейных моделей для

комплексных сигналов. Введём комплексные наблюдения

y(i) y1(i) jy2 (i)

и комплексную модель

сигнала

cT (Ti), определяемую

комплексным вектором

параметров

cT (c ,...,c )

и

комплексной

1

m

базисной

функцией T (Ti) ( (Ti),..., (Ti)),

с c

jc

,

(Ti)

(Ti) j

(Ti),

r 1,..., m,

1

m

r

1r

2r

r

1r

2r

i 0,1,..., N 1. Функционал с

использованием

суммы

произведений

сопряженных

комплексных

множителей

N 1

S(c, Y ) ( y(i) cT (Ti))*( y(i) cT (Ti)).

(2.4.8)

i 0

комплексную разность функции наблюдения и модели

Y (c) Y Xc.

Воспользовавшись введёнными

векторно-матричными переменными, но в комплексной форме, представим функционал S(Y , c) (2.4.8)

S(Y , c) Y *T (c) Y (c) (Y Xc)*Т (Y Xc).

С учётом равенства Y*T Xc c*T X *T Y запишем

S(Y , c) (Y Xc)*Т (Y Xc)

	(Y * X *c* )T (Y Xc) Y *T Y 2Y *T Xc c*T X *T		(2.4.9)
			Xc.
	=0
Минимальное значение этой квадратичной формы (2.4.9) достигается при
	c ( X *T X ) 1 X *T Y.	(2.4.10)

Оценка с из (2.4.10) может быть найдена с помощью решения системы линейных уравнений (в лекциях

A=D)

	( X *T X ) c	X *T Y ,	Dc	b.	(2.4.11)
Коэффициенты матрицы D вычисляются в виде скалярных				произведений	векторов *r (Ti),	s (i),
i 0,1,..., N 1:
	N 1
	drs *r (Ti) s (Ti) ,		r, s 1,..., m.		(2.4.12)
	i 0
Коэффициенты вектора b (коэффициенты Фурье)		вычисляются в виде скалярных произведений векторов
*r (Ti),	y(i), i 0,1,..., N 1:
	N 1
	br *r (Ti) y(i) ,		r 1,..., m.		(2.4.13)

i 0

Если базисные функции ортогональны, то нахождение параметров модели упрощается. Матрица D будет диагональной с элементами

d	rr	2	,	r 1,..., m, d	rs	0,	r s.
		r

Оптимальные параметры модели выразятся через коэффициенты Фурье

		1	N 1		br
	сr		*r	(Ti) y(i)		,	r 1,..., m.	(2.4.14)
		2
					2
			i 0
		r			r

4

3. Модели сигналов на основе действительного и комплексного ряда Фурье.

Действительный случай. Рассмотрим построение моделей сигналов на основе действительного ряда Фурье.

Пусть наблюдения cигнала заданы в виде действительной функции y(t)				на конечном интервале времени
0 t T0. {Будем полагать, что для рассматриваемого сигнала y(t)				выполнены сформулированные
условия сходимости. }
Выбирается модель для указанного сигнала в форме действительного ряда Фурье следующего вида
		a0
	yM (c, t)		(al cos lt bl sin lt).	(2.5.1)
	2		l 1
модельные частоты l l,	2 /Т0 , l 2 l T0 и определяются длиной интервала наблюдения,

модельные синусоиды располагаются с шагом по частоте ,						который зависит от Т0 . Вектор параметров
модели имеет бесконечную размерность,		сT (a , a , a ,....., b , b ,....),							b 0.	{Благодаря выбору
			0	1	2	1	2		0
частотного параметра оказывается, что на интервале времени Т0								укладывает целое число периодов
базисных функций cos lt cos lt и	sin lt sin lt. Вследствие этого, указанные} базисные функции
являются ортогональными.
Функционал для решения задачи аппроксимации функции наблюдений y(t)									на основе сформированной
модели имеет вид
T0		a						2
S(c, y)	y(t)	0	(al	cos lt bl sin lt) dt.
		2
0			l 1

Нахождение вектора параметров модели сводится к минимизации указанного функционала, который, очевидно, является квадратичным по с:

с arg{min S(c, y)}, c T	(a , a , a ,....,b , b ,...).
c	0	1	2	1	2
Устремим число базисных функций в бесконечность,	L .		Естественно, можно сразу записать, опустив

знак , формулы для оптимальных параметров модели, которые являются известными коэффициентами разложения Фурье:

	a	2	T0	y(t) cos tdt,	b		2	T0	y(t)sin tdt,	l 0,1, 2,... .
		T					T
	l			l	l				l
		0	0				0	0

В силу ортогональности базисных функций модели ряда Фурье мощность P сигнала, сформированного на основе ряда Фурье, слагается из мощностей составляющих синусоид Pl , мощность для l-й синусоиды определяется амплитудами

			A2
	P Pl ,	Pl	l	,	Al2 al2 bl2 ,	l 0, 1, 2,... .
			2
	l 1

{Благодаря ортогональности данного базиса для рассматриваемой модели возможно представление дискретного спектра мощности в виде бесконечной последовательности равноотстоящих на по оси частот значений Pl . }

Комплексный случай. Пусть произведено наблюдение комплексной						функции y(t) =			y1(t)+jy2(t) на
интервале 0 t T0 , модель сигнала представится комплексным рядом Фурье
	l
yM (c, t) cl e j lt ,			2 /Т0		l l.		(2.5.5)
	l
Комплексный вектор параметров модели имеет бесконечную размерность cT (...,c								, c	, c , c , c ,...).
							2	1	0 1 2
Функционал остаточной суммы примет вид
Т0		l	*		l
S(c, y)	y(t)	с l e j lt		y(t)	cl e j lt dt.		(2.5.6)
0		l			l

5

Так же как и для разд. 2.5.1, ограничимся конечным числом комплексных модельных синусоид, которые составляют модель; пусть число модельных синусоид равняется L. В этом случае вектор базисных функций для модели (2.5.5) имеет размерность (2L 1, 1) и выглядит следующим образом

T (t) e j Lt , e j (L 1)t ,..., e j 1t , e j 0t , e j 1t ,..., e j (L 1)t , e j Lt .

на интервале времени 0 t T0 составляющие базис функции ортогональны.

Оптимальные параметры модели cl ,				обеспечивающие минимум функционала (2.5.6) {после того как
сделаны необходимые выкладки и предельный переход L определяются следующими интегралами
(опущен знак )}:
		T
cl	1	0	y(t)e j lt dt,	l .	(2.5.7)
	T
0		0

{Пусть для рассматриваемой функции сигнала y(t) выполняются сформулированные в разд. 2.5.1 условия сходимости с учётом комплексности. Тогда на оптимальных cl из (2.5.7), очевидно, должно выполняться равенство }

l
y(t) cl e j lt .	(2.5.8)

l

Мощность l-й комплексной модельной синусоидальной функции вычисляется интегрированием на интервале 0 t T0 :

y (t) (c

jc

)(cos t j sin t),

y*(t) (c

jc

)(cos t

j sin t),

l

1l

2l

l

l

l

1l

2l

l

l

1

T0

l

Pl

yl (t) yl* (t)dt (c12l c22l ) cl*cl ,

P Pl .

T

0

0

l

Благодаря ортогональности используемого комплексного базиса общая мощность сигнала представляется в виде суммы мощностей составляющих как для положительных, так и отрицательных частот.

6

4.Интеграл Фурье. Свойства интеграла Фурье. (ПФ-преоб-е Фурье, ФС-физический смысл)

Интеграл Фурье реализуется на основе рассмотрения комплексного ряда Фурье для бесконечного временного интервала; Симметричен относительно нуля,меняются только фазовые соотношения

временной интервал симметричным T0 /2 t T0 /2, пусть этот интервал расширяется

T0	k,	k 1,	2,...,		2	l	2	l	l	.
2				l	T0		2 k		k

Запишем коэффициенты разложения комплексного ряда Фурье для расширяющегося временного интервала T0 2 k

		1	k		j	l	t
c				y (t)e				dt,	y (t)
						k
l,k		2 k		k					k
			k

Подставим выражение cl,k в yk (t)

Устремим k , обозначим lk

l

l

cl,k e j

t .

k

l

l

j

l

t

1

k

j

l

: y (t)

e

k

y ( )e

k

d .

2 k

k

k

l

k

1

d , l k , получим в пределе y(t)

2

		1
	Сформируем интегралы C( j )			y(t)e j t dt,	y(t)	С( j )e j t d .
		2

Функцию C( j ) называют интегралом Фурье, или преобразованием Фурье для

j j t y( )e d e d .

y(t). прямое и обратное

преоб-е Фурье. Сигнал представляется как во временной области при традиционном анализе, так и в частотной области в виде непрерывных коэффициентов разложений Фурье C( j ), .

ФC C( j ) :Преоб-е Фурье C( ) -предельная функция коэффициентов комплексного ряда Фурье.

Функция C( ) в общем случае является комплексной функцией частоты и допускает следующие представления:

C( ) C ( ) jC ( ),

C( )

C( j )

e j ( ) ,

1

2

( )

где C1( ) и C2 ( ) – действительные и мнимые части;

C( j )

,

– модуль и фаза преобразования

Фурье.

Св-ва:

1. Линейность. Пусть функция y(t) представляет собой взвешенную сумму функций

ys (t), для которых

k

заданы их преобразования Фурье Cs ( j ) : y(t) s ys (t),

Cs ( j ) F [ys

(t )]преоб.

-е Фурье C( j ) для

s 1

y(t) вычисляется

как

взвешенная

сумма

преобразований

Фурье

Cs ( j ) :

C( j ) F[ y(t)],

k

C( j ) sCs ( j ).

s 1

2. Сдвиг Пусть –

масштабирующий

множитель,

преобразующий функцию y(t)

в y(t) y( t), и

1

1

C( j ) F[ y(t)]. C

( j ) -?

С( j )

y(t)e j t dt,

С

( j )

y( t)e j t dt.

2

2

Пусть: t1 t, dt dt1

, сделаем подстановку в C

( j ) и выразим C( j )

через C( j ) :

1

y(t1)e j

t1

1

1

j

С

( j )

dt1,

C

( j )

С

.

2

3. СдвигПусть задано преобразование Фурье для функции

y(t): C( j ) F[ y(t)]. Введём запаздывание

(сдвиг по времени) для функции y(t),

сформируем y(t) y(t ).

7

			1		1
				y(t )e j t dt		y(t )e j (t )e j dt,			( j ) C( j )e j .
C		( j )					C
			2		2
преобразование Фурье для функции y(t), умноженной на e j 0t , сдвигается по частоте										y(t) y(t) e j 0t ,

C( j ) C( j( 0 )).

4. Прео-е Фурье от комплексной синусоиды y(t) e j 0t требует предварительного определения -функции. { Импульсной -функцией называется такая функция, которая удовлетворяет следующим двум условиям:

1)	(x) 0	для x 0 и (x) для x 0;
2)	(x) 1		для любого 0.

Импульсная -функция может рассматриваться как предел обычной функции (х) при 0. Например,

(x) 1/ 2 для		х		и (x) 0 для		х		.

Для -функции устанавливается важное равенство:

b

(x0 ), a x0 b;

(x) (x x0 )dx

b,

a

0, x0 a, x0

если (x)

непрерывна в точке x0 и a b. }

С учётом сделанного определения можно записать преобразование Фурье для y(t) e j 0t :

C( j )

1

e j 0t e j t dt ( ).

y(t)

( )e j t d e j 0t .

2

0

0

ФС: если синусоида определена на

интервале, ее энергия бесконечна. След-во в ПФ везде нули.

6. ПФ для симметричного единичного импульса:

T0

T0

1

T0 /2

1

sin (T0 / 2)

sin (T0

/ 2)

y(t) 1,

y(t) 0,

C( j )

1 e j t dt

t

,

t

,

2

2

2 T /2

2

0

sin

T0

T0

2 .

2

T0

2

Едичный импульс симметричен

преобразование Фурье C( j ) является действительной функцией.

7. ПФ для произведения функций y(t) x(t)z(t),

Cx ( j ),

Cz ( j ) – ПФ x(t), z(t).

1

1

C

( j )

y(t)e j t dt

С

( j )e j 1t d

C

( j )e j 2t d

e j t dt.

y

2

2

x

1

1

z

2

2

Изменив порядок интегрирования, с учётом выражения интеграла Фурье для комплексной синусоиды получим

1

2

d C

( j )

C

( j )d

e j 1t e j 2t e j t dt

d C

( j )

C

( j )d ( )

1 x

1

z

2 2

1 x

1

z

2 2

1 2

Cy(w)=

Cx ( j 1)Cz ( j( 1))d 1. Преобразование Фурье от произведения функций равняется свёртке

преобразований Фурье сомножителей.

8

5.Дискретизация непрерывных сигналов. Теорема Котельникова. Кажущиеся частоты и протимаскировочная фильтрация.

Положим, что задан исходный непрерывный сигнал y(t), t , который является в общем случае комплексным и определённым в бесконечных временных пределах. Для данного сигнала производится дискретизация во времени, где T – интервал дискретизации; y(Ti) – дискретные значения непрерывного сигнала; fd 1 T – частота дискретизации, Гц; d 2 fd – круговая частота дискретизации. При фиксированном временном интервале T, дискретизация осуществляется равномерно для моментов времени ti Ti. {Дискретизация может производиться неравномерно для произвольных моментов времени ti и её результатом служит соответствующая последовательность дискретных значений непрерывного сигнала y(ti ). Здесь} будем рассматривать только равномерную дискретизацию во времени; пренебрежём погрешностями, возникающими из-за дискретизации по уровню.

Задача восстановления непрерывного сигнала y(t) по его дискретным значениям y(Ti) задача интерполяции. Восстановление сигнала здесь состоит в том, что по бесконечной последовательности дискретных значений сигнала y(Ti), i , необходимо найти значения непрерывного сигнала для промежуточных моментов времени t Ti.

Исходный сигнал y(t) принадлежит к некоторому заданному классу функций; допустим, что можно

подобрать, у базисные функции i (t, T ),	t , i . В качестве восстановленного сигнала
y (t) для y(t) примем предел
N
y(t, N) y(Ti) i (t, T ), y (t)	lim y(t, N ).
i N	N
Задача восстановления может считаться успешно решённой, если будет выполнено равенство
y (t) y(t).	(3.4.1)

{Возможность восстановления сигнала по его дискретизованным значениям зависит от частотных свойств сигнала и выбранной частоты дискретизации. Высокая частота дискретизации, очевидно, позволит осуществить восстановление сигнала; для низкой частоты дискретизации восстановление в ряде случаев

проблематично. }
	Появление		«кажущихся»			частот
	Неправильно		выбранная частота
	дискретизации,				которая	не
	согласована			с	частотными
	свойствами сигналов, приводит к
	появлению			так	называемых
	«кажущихся»				частотных
	составляющих. Разберём пример, в
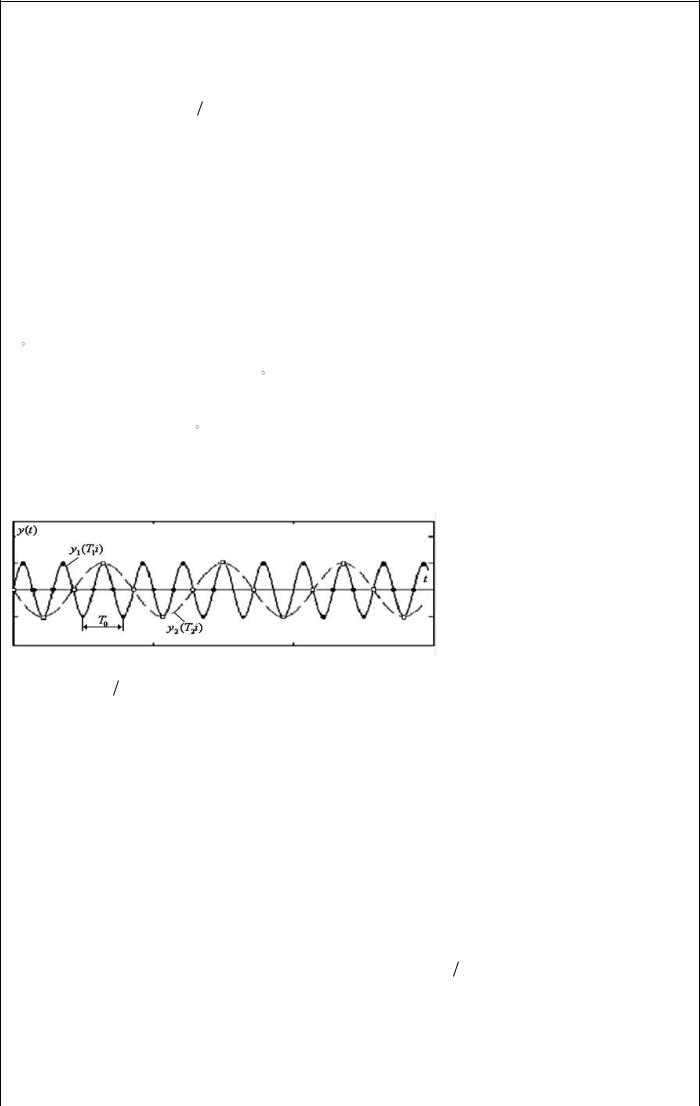
котором дискретизации подвергается непрерывный синусоидальный сигнал		вида			y(t) sin 2 f0t с
периодом T0 1 f0 . На рис. исходный сигнал y(t) изображен сплошной линией.				Подвергнем исходный

непрерывный сигнал y(t) дискретизации с частотой fd1 4 f0 – четыре точки дискретизации на один период T0 , интервал дискретизации T1 1/ 4 f0 , T1 T0 / 4. Дискретизованные значения исходного сигнала отмечены чёрными жирными точками.Уменьшим частоту дискретизации, примем её равной fd 2 4 / 3 f0 , период дискретизации Td 2 4 / 3T0 , эти точки дискретизации отмечены кругами на пунктирной линии. В первом случае частота дискретизации больше двойной частоты сигнала, дискретизованный сигнал воспринимается как сигнал с периодом Tk1 T0 и его «кажущаяся» частота совпадает с частотой исходного сигнала fk1 f0 . Во втором случае частота дискретизации меньше двойной частоты сигнала, дискретизованный сигнал воспринимается как сигнал с периодом Tk 2 3T0 и его кажущаяся частота меньше частоты исходного сигнала fk 2 1/ Tk 2 f0 / 3. Вследствие неудачного выбора частоты дискретизации имеет место очень сильное искажение информации, «кажущаяся» частота сигнала меньше частоты исходного сигнала, что и видно из рис. 3.4.1.

Рассмотрим более детально существо проблемы возникновения «кажущихся» частотных составляющих

для дискретной синусоидальной функции y(i) sin(2 f0Ti). Введём частоту Найквиста,		равную половине
частоты дискретизации, fN 1/ 2T. Всегда можно представить	f0 fN p q, где p	– целое,		q		1.
Учитывая равенство 2 f0Ti ( p q)i, запишем:

y(i) sin ( p q)i sin pi cos qi cos pi sin qicos pi sin qi.

9

1) частота Найквиста больше частоты сигнала –		р 0, тогда f0 / fN 1 и справедливо: y(i) sin qi
sin 2 fk1Ti. Следует, что 2 fk1T q,	fk1 fN q	и fk1 f0 – «кажущаяся» частота совпадает с частотой

исходного сигнала. 2) частота Найквиста меньше частоты сигнала – в частном случае положим p четным, f0 / fN 1, при этом fk 2 fN q f0q / ( p q) и fk 2 f0. Оказывается, что во втором примере «кажущаяся» частота меньше частоты исходного сигнала. Данные примеры позволяют сделать заключение, что для совпадения частоты сигнала и «кажущейся» частоты, частота Найквиста должна быть больше частоты

дискретизуемого сигнала.

Теорема Котельникова

Установим возможность точного восстановления непрерывных сигналов по их дискретным значениям. В

рамках теоремы Котельникова рассматриваются сигналы, принадлежащие к классу сигналов с финит-

ным преобразованием Фурье. Сигнал	y(t) имеет финитное преобразование Фурье, обозначаемое как
С f ( j ), если: 1) С f ( j ) 0 для всех	частот				; 2) С f ( j ) тождественно не равно нулю для частот

, где – верхнее значение частоты сигнала – полоса сигнала. Теорема Котельникова утверждает, что для сигналов с финитным преобразованием Фурье возможно точное восстановление сигнала по дискретным наблюдениям, если круговая частота дискретизации d удовлетворяет строгому неравенствуd 2 , где 2 f p , f p – полоса сигнала, Гц, fd 2 f p .

Представим исходный сигнал y(t) на основе обратного преобразования Фурье, если С f ( j ) – финитное

преобразование Фурье:

y(t) C f ( j )e j t d .

Возьмём , разложим функцию С f ( j ) в комплексный ряд Фурье на данном интервале ( , ) :

		2					2
	С f ( j ) c fl e j		l , c fl	1		C f ( j )e j		l d .
		2					2		(3.4.2)
				2
	l
	Учитывая введённое соотношение между величинами и , запишем
	y(t) C f ( j )e j t d				C f ( j )e j t d .				(3.4.3)

Справедливо равенство, вытекающее из (3.4.2), (3.4.3), связывающее дискретные значения сигнала и

коэффициенты фурье-разложения

2

2

c

1

y

2

l

.

fl

Подставим коэффициенты фурье-разложения c f l

в выражение для С f ( j ) из (3.4.2):

y

2

l e j

2

С f ( j )

1

l .

2

(3.4.4)

2

l

2

1

2

j

2

l

Подставим выражение (3.4.4) в ( 3.4.3) y(t)

y

l

e

2

e j t d .

l 2

2

j

l t

2

Переменим порядок интегрирования и суммирования y(t)

1

y

2

e

d .

2

l

2

2

l

Сделаем замену 2 / 2 T, при этом частота дискретизации окажется равной d

2 , и переобозначим

индексы суммирования l i :

2sin (t Ti) .

y(t)

1

y(Ti) e j(t Ti) d .

e j(t Ti) d

Сигнал

y(t) может быть представлен в

i 2

(t Ti)

виде разложения по базисным функциям i (t, T )

с весовыми коэффициентами y(Ti) :

sin (t Ti)

y(t) y(Ti) i (t,

T ),

i (t,T )

.

i

(t Ti)

Таким образом, в соответствии с теоремой Котельникова сигнал с финитным преобразованием Фурье с полосой при выборе частоты дискретизации d 2 допускает точное восстановление –

выполнение равенства (3.4.1).

Противомаскировочные фильтры Устранение эффекта маскировки (наложения) может быть реализовано двумя способами.

10