4 семестр / Задание №2 Численное решение одномерного уравнения теплопроводности

Задание № 2

ЧИСЛЕННОЕ РЕШЕНИЕ ОДНОМЕРНОГО

УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ

Цель работы — изучение разностных схем для численного решения уравнения теплопроводности, численное решение одномерного уравнения теплопроводности по схеме «с полу­суммой».

ПОСТАНОВКА ЗАДАЧИ

Распространение тепла в одномерной области описывается уравнением эволюционного типа

(1)

с начальным условием

и краевыми условиями

Здесь u — температура, х — координата, t — время, a²— коэффициент теплопроводности; функция f(x,t) описывает источ­ники тепла.

Уравнением описывается также процесс диффузии газа; при этом u — плотность газа, a² = D —коэффициент диффузии, f(x, t) — внутренние источники газа (выделение и поглощение).

Заметим, что для существования и единственности решения уравнения не требуется согласования начального и краевых условий, т. е. не требуется выполнения равенств ₁(0) = u⁰(0), ₂(0) = u⁰(l), иначе говоря, допускаются разрывы u(x, 0) на границах в начальный момент t = 0.

Заменяя производные конечными разностями, построим следующие разностные схемы:

(2)

(3)

(4)

где

Соответствующие им шаблоны приведены на рис. 1.

Рис. 1. Расположение узлов разностных схем для одномерного уравнения теплопроводности

Первая схема (2) является явной, имеет погрешность аппроксимации O(, h²) и устойчива при выполнении условия 0    0.5h²/a². Вторая схема (3) является неявной, имеет такую же погрешность аппроксимации и безусловно устойчива. Если для увеличения пространственного разрешения потребуется в первой схеме уменьшить шаг h на порядок, то шаг  для сохранения устойчивости придется уменьшить на два порядка, а число арифметических операций и длительность счета, составляющие О(1/(h)) = О(h^–3) = О(N³), возрастут на три порядка. Поэтому, несмотря на простоту вычислений, явными схемами стараются не пользоваться в задачах, в которых требуется высокое пространственное разрешение, т. е. малый шаг h. Неявная разностная схема (3) лишена этого недостатка.

В обеих разностных схемах  — низкий, т. е. первый порядок погрешности по . Рассмотрим теперь схему (4), построенную на третьем шаблоне (см. рис. 1)), которую называют разностной схемой «с полусуммой», или схемой Кранка–Николсона. Можно показать, что данная разностная схема имеет более высокий порядок погрешности аппроксимации О(², h²) и безусловно устойчива.

Преобразуем её к следующему виду:

т.е.

Решение на каждом временном шаге находится методом прогонки (смотри задание № 5 третьего семестра). Результаты u_j (j = 0,1,...,N) выдаются через каждые М = 10 ÷ 50 временных шагов. Прогонка строится в два этапа.

Первый этап — вычисление прогоночных коэффициентов по рекуррентным формулам (прямой ход)

Второй этап — вычисление , (обратный ход)

ВАРИАНТЫ ЗАДАНИЙ

ВАРИАНТЫ НАЧАЛЬНЫХ УСЛОВИЙ

ВАРИАНТЫ КРАЕВЫХ УСЛОВИЙ

(b= 0.1 ÷ 2)

ВАРИАНТЫ ФУНКЦИЙ ИСТОЧНИКОВ ТЕПЛА

(x=0.1÷ 2)

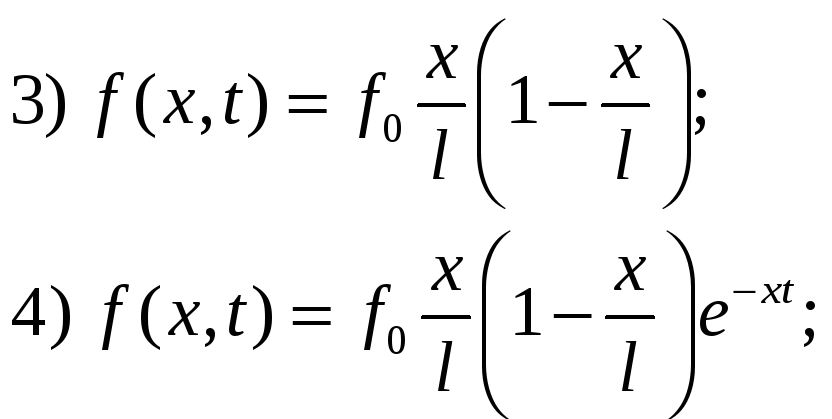
ПРОГРАММИРОВАНИЕ

Функции f, φ₁, φ₂ целесообразно оформить в виде под­программ-функций. Для хранения u_j, и , следует отвести два одномерных массива. Шаг τ можно оценить из условия τа²/h = 0.2 ÷ 1, число пространственных шагов N – несколько десятков, число временных шагов – несколько сотен. Особенности прогонки обсуждались в задании № 5 третьего семестра, организация выдач – в предыдущем задании.

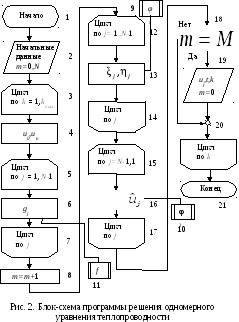
Блок-схема программы представлена на рис. 2. В блоке 4 задаются граничные условия, в цикле 5-6-7 вычисляются правые части уравнения, в 12-17 организован метод прогонки.

Для проверки программы можно предварительно решить тестовую задачу, полагая

и исследуя установление стационарного состояния

СОДЕРЖАНИЕ ОТЧЕТА

Отчет должен содержать:

• формулы и параметры для конкретного варианта;

• текст программы;

• результаты решения.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Каков порядок погрешности приведенных разностных схем?

2. Покажите, что неявные разностные схемы (3), (4) безусловно устойчивы.

3. Как строится решение разностной схемы (4)?

4. Изобразите расположение узлов («шаблон»), на котором построена разностная схема (4).

7