НГА Украины Методические материалы Кафедра СА и У Лекции по основам дискретной математики 31

Раздел 2. Основы теории графов

2.1. Основные положения

Теорию графов начали разрабатывать для решения некоторых задач о геометрических конфигурациях, состоящих из точек и линий.

Определение графа можно дать как совокупности двух множеств V(точек) и E(линий, дуг), между элементами которых определено отношение инцидентности, причем каждый элемент е  E инцидентен равно двум элементам v’,v”  V. Элементы множества V называются вершинами графа G , элементы множества Е – его ребрами. Вершины и ребра графа G называют еще его элементами и вместо е  Е и v V пишут e  G и v  G.

В некоторых графах инцидентные ребру вершины неравноправны, они должны, например, рассматриваться в определенном порядке. Тогда каждому из ребер можно приписать направление от первой из инцидентных вершин ко второй. Направленные ребра часто называют дугами, а содержащий их граф – ориентированным. В противном случае

( инцидентные ребру вершины равноправны) граф будем называть неориентированным. Для ориентированного графа

Начало конец

1 2

Дуга: выходит входит

Наглядное представление о графе можно получить, если представить себе некоторое множество точек плоскости Х, называемых вершинами, и множество направленных отрезков U, соединяющих все или некоторые из вершин и называемых дугами. Математически граф G можно определить как пару множеств Х и U. G=(X,U) (1)

Н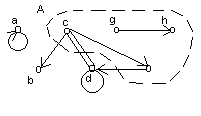а рисунке изображен граф, вершинами которого являются точкиa, b, c, d, e, g, h, а дугами - отрезки (a,a), (c,b), (c,d), (c,e), (d,c), (d,d), (e,d), (g,h).

П

Рис.2.1 – Изображенние

графа

римерами графов являются отношения отцовства и материнства на множестве людей (родовое дерево), карта дорог на местности, схема соединений электрических приборов, отношении превосходства одних участников турнира над другими и т.п. Иногда бывает удобно дать графу другое определение. Можно считать, что множество направленных дуг U, соединяющих элементы множества Х, отображает это множество само в себя. Поэтому можно считать граф заданным, если дано множество его вершин Х и способ отображения Г множества Х в Х. Т.о., граф G есть пара (Х, Г), состоящая из множества Х и отображения Г, заданного на этом множестве G=(X,Г).

Так, для графа, изображенного на рис.2.1 отображение определяется следующим образом:

Г_a=a; Г_b=; Г_c={b,d,e}; Г_d={c,d}; Г_e=d; Г_g=h; Г_h=.

Нетрудно заметить, что данное определение графа полностью совпадает с определением отношения на множестве.

Введем некоторые понятия и определения, служащие для описания различных видов графов.

Подграфом G_A графа G=(X,Г) называется граф, в который входит лишь часть вершин графа G, образующих множество А, вместе с дугами, соединяющими эти вершины, например, очерченная пунктиром область А на рис.2.1. Математически подграф обозначается следующим образом:

G_A=(A,Г_A), где АХ, Г_АХ=(Г_Х)А (2.1)

Частичным графом G_ по отношению к графу G=(X, Г) называется граф, содержащий только часть дуг графа G, т.е. определяемый условием:

G_=(X, ), где x  Г_X (2.2)

Например, пусть G=(X,Г) - карта шоссейных дорог Украины. Тогда карта шоссейных дорог Днепропетровской области представляет собой подграф, а карта главных дорог Украины - это частичный граф.

Другими важными понятиями для графа является понятие пути и контура. Дуга, соединяющая вершины a и b, и направленная от а к b обозначается u=(a,b).

Определения.

Путем в графе G называют такую последовательность дуг =(u₁,...,u_k) , в которой конец каждой предыдущей дуги совпадает с началом следующей. Путь , последовательными вершинами которого являются вершины a,b,...,m, обозначается через =(a,b,...,m).

Длиной пути =(u₁,...,u_k) называют число l()=k, равное числу дуг, составляющих путь. Иногда каждой дуге u_i приписывают некоторое число l(u_i), называемое длинной дуги. Тогда длинна пути определяется как сумма длин дуг, составляющих путь

_k

l ()= l(u_i) (2.3)

^I=1

Путь, в котором никакая дуга не встречается дважды, называется простым. Путь, в котором никакая вершина не встречается дважды, называется элементарным.

Контур - это конечный путь =(x₁,...,x_k), у которого начальная вершина х₁ обязательно совпадает с конечной х_k. При этом контур называется элементарным, если все его вершины различны (за исключением начальной и конечной, которые совпадают). Контур единичной длинны, образованный дугой вида (а, а) называется петлей. Так, например, на рис. 1 (e, d, c, b) - путь, а (c, e, d, c) - контур, (d, d) - петля.

Иногда графы удобно представлять в виде некоторых матриц, в честности в виде матриц смежности и инцидентности. Предварительно дадим два определения.

Вершины x и y являются смежными, если они различны и если существует дуга, идущая из x в y.

Дугу u называют инцидентной вершине х, если она заходит в эту вершину или исходит из нее.

Обозначим через х₁,...,х_n вершины графа, а через u₁,...,u_m его дуги. Введем числа:

1, если имеется дуга, соединяющая вершину i с

r_ij =  вершиной j; (2.4)

0, если такой дуги нет.

Квадратная матрица R=[r_ij] порядка (nxn) называется матрицей смежности графа.

Введем числа :

 +1, если u_j исходит из x_i

S_ij=  -1, если u_j заходит в x_i (2.5)

 0, если u_j не инцидентна x_i

Тогда матрица S=[S_ij] порядка (nxm) называется матрицей инцидентности для дуг графа.

Матрицы инцидентности в описанном виде применимы только к графам без петель. В случае наличия в графе петель эту матрицу следует расчленить на две полу матрицы: положительную и отрицательную.

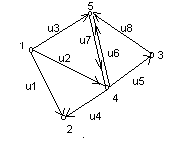
На рис.2.2 приведен граф без петель, для которого матрицы смежности и инцидентности имеют следующий вид:

Матрица смежности.

i j	1	2	3	4	5
1	0	1	0	1	1
2	0	0	0	0	0
3	0	0	0	0	1
Ри.2.2. 4	0	1	1	0	1
5	0	0	0	1	0

Рис.2.2 – Граф без петель

Матрица инцидентности

i j	1	2	3	4	5	6	7	8
1	1	1	1	0	0	0	0	0
2	-1	0	0	-1	0	0	0	0
3	0	0	0	0	-1	0	0	1
4	0	-1	0	1	1	1	-1	0
5	0	0	-1	0	0	-1	1	-1

Обычно рассматриваемые графы конечны, т.е. конечны множества их элементов

( вершин и ребер). Поэтому конечность этих графов не будет специально оговариваться.

Примеры ориентированных графов:

а в с

d e f g к

(кратные ребра)

Рис.2.3 - Примеры ориентированных графов

В приведенных примерах вариант "в" представляет граф с пустым множеством ребер. Граф "е" иллюстрирует недостижимость двух вершин, а "g" – граф с петлей.