
- •1.6 Полярная и цилиндрическая системы координат
- •1. Полярная система координат.
- •1. Цилиндрические координаты точки в пространстве.
- •2.1 Понятие вектора
- •4.3 Проекция вектора на направление другого вектора
- •5.1 Определение векторного произведения
- •5.2 Вычисление векторного произведения двух векторов
- •5.3 Свойства векторного произведения
- •7.2 Плоскость
- •7.3 Прямая в пространстве
- •7.4 Взаимное расположение прямых и плоскостей в пространстве
- •8.1 Определение предела
- •8.2 Свойства пределов
- •8.3 Бесконечно малые и бесконечно большие величины
- •8.4 Первый замечательный предел
- •9.1 Определение функции одной переменной
- •9.2 Способы задания функции
- •9.3 Основные свойства функции
- •9.4 Основные элементарные функции. Их графики
- •10.1 Односторонние пределы
- •10.2 Определение непрерывности функции
- •10.2 Классификация точек разрыва функции
- •11.1 Определение второго замечательного предела
- •11.2 Следствия из второго замечательного предела
- •13.1 Определение приращения функции
- •13.2 Определение производной функции
- •13.3 Свойства производной функции
- •13.4 Производные основных функций
- •13.5 Производные обратных функций
- •14.1 Определение гиперболических функций
- •14.2 Производные гиперболических функций
- •14.3 Производные сложных функций
- •14.4 Производные высших порядков
- •15.1 Параметрическое задание функций
- •15.2 Производные параметрических функций
- •15.3 Уравнения касательной и нормали к графику функции в заданной точке
- •16.1 Определение дифференциала. Его геометрический смысл
- •16.2 Свойства дифференциала
- •17.4 Теорема Лагранжа
- •17.5 Правило Лопиталя
- •17.6 Производная от функции в степени функции
- •18.1 Определение экстремума
- •18.2 Условия существования экстремума
- •18.3 Наибольшее и наименьшее значения функции на отрезке
- •18.4 Точки перегиба графика функции
- •19.1 Вертикальные асимптоты
- •19.2 Наклонные асимптоты
- •20.1 Определение степенного ряда
- •20.2 Ряд Тейлора
- •20.3 Ряд Маклорена
ЛЕКЦИИ ПО ВЫСШЕЙ МАТЕМАТИКЕ ДЛЯ СПЕЦИАЛЬНОСТЕЙ МЭС; МТС , 1-Й СЕМЕСТР
(32 ЧАСА)
ЛЕКЦИЯ 1
ДЕКАРТОВА СИСТЕМА КООРДИНАТ НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ
Понятие числовой оси
Числовой осью называется прямая линия, на которой заданы:
начало (обозначается О );
направление (обозначается стрелкой);
масштабная единица.

. .
О 1 x
Ox – числовая ось.
Всякому действительному числу соответствует единственная точка числовой оси, всякой точке числовой оси соответствует единственное действительное число. При этом данное действительное число называется координатой соответствующей ему точки числовой оси.
Пример. Построить точки:
![]()
Решение

. . . .
![]() 0
0
![]()
![]() x
x
Декартова прямоугольная система координат на плоскости
Декартовой
прямоугольной системой координат на
плоскости называется совокупность двух
взаимно перпендикулярных
числовых осей, имеющих общее начало.
Обозначается:
![]() .
Всякой точке плоскости соответствует
упорядоченная пара чисел
.
Всякой точке плоскости соответствует
упорядоченная пара чисел![]() .
Эта пара чисел называетсякоординатами
данной точки на плоскости.
.
Эта пара чисел называетсякоординатами
данной точки на плоскости.
Пример. Построить точки:
![]()
Решение
 y
y
![]() .
3
.
3
 .
.![]()
 O
2
3 x
O
2
3 x





![]() .
.![]()
Декартова прямоугольная система координат в пространстве
Декартовой
прямоугольной системой координат в
пространстве называется совокупность
трех
взаимно перпендикулярных
числовых осей, имеющих общее начало.
Обозначается:
![]() .
Всякой точке трехмерного пространства
соответствует упорядоченная тройка
чисел
.
Всякой точке трехмерного пространства
соответствует упорядоченная тройка
чисел![]() .
Эта тройка чисел называетсякоординатами
данной точки в пространстве.
.
Эта тройка чисел называетсякоординатами
данной точки в пространстве.
Пример.
Построить точку
![]() .
.
Решение

 z
z
5
M
![]()
0 y
.
3
x
Расстояние между двумя точками
Рассмотрим
на плоскости две точки:
![]() и
и![]() .
Расстоянием между этими точками является
отрезок
.
Расстоянием между этими точками является
отрезок![]() прямой, соединяющей эти точки. Найдем
длину этого отрезка, применив теорему
Пифагора. Перед нами треугольник,
катетами которого являются отрезки,
длины которых соответственно равны:
прямой, соединяющей эти точки. Найдем
длину этого отрезка, применив теорему
Пифагора. Перед нами треугольник,
катетами которого являются отрезки,
длины которых соответственно равны:
![]() и
и
![]() , а гипотенузой является искомый отрезок
, а гипотенузой является искомый отрезок![]() .
Следовательно, можем записать:
.
Следовательно, можем записать:
![]() (1.1)
(1.1)
Таким образом, расстояние между двумя точками равно квадратному корню из суммы квадратов разностей соответственных координат этих точек.
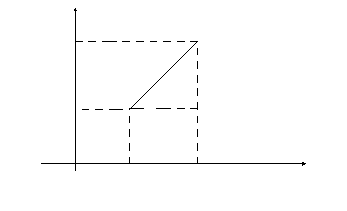 y
y
![]()
![]()
![]()
![]()
O
![]()
![]() x
x
Согласно
записанному положению, формула (1.1) для
точек
![]() и
и![]() ,
заданных в пространстве имеет вид:
,
заданных в пространстве имеет вид:
![]() (1.2)
(1.2)
Деление отрезка в заданном отношении
Рассмотрим
на плоскости две точки:
![]() и
и![]() .
Найдем координаты точки
.
Найдем координаты точки![]() ,
делящей отрезок
,
делящей отрезок![]() в отношении
в отношении![]() ,
т.е.
,
т.е.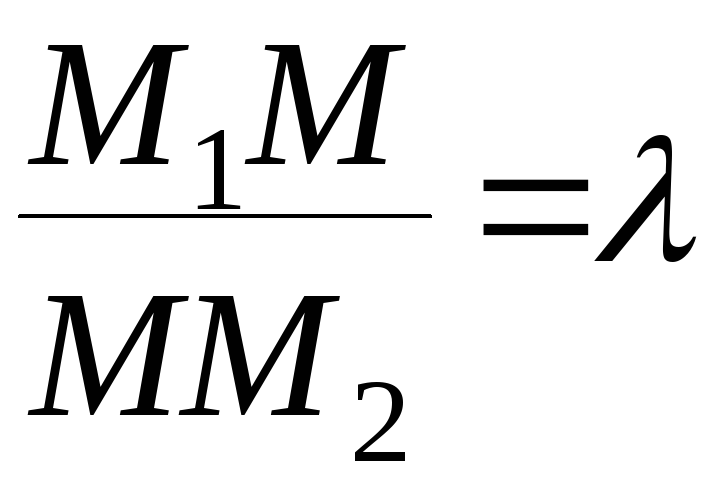 .
.

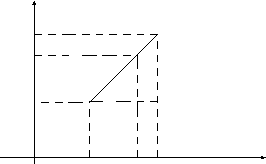 y
y
![]()
![]()
y M
![]()
![]()
O
![]() x
x
![]() x
x
Согласно теореме о пропорциональности длин отрезков, отсекаемых параллельными прямыми на сторонах угла, можем записать:
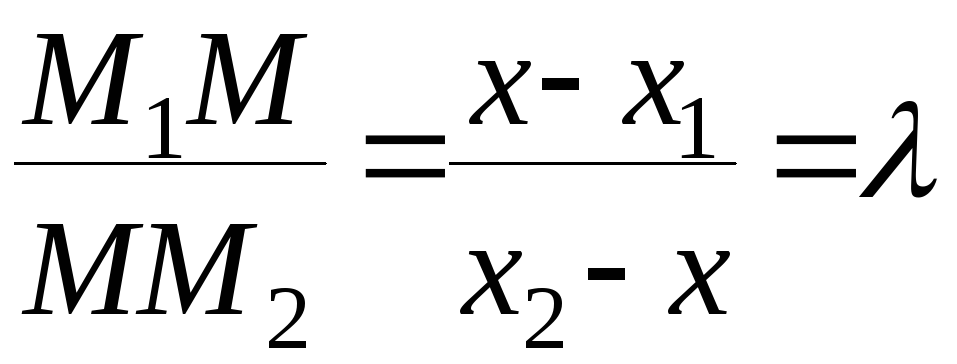 .
Откуда следует, что
.
Откуда следует, что
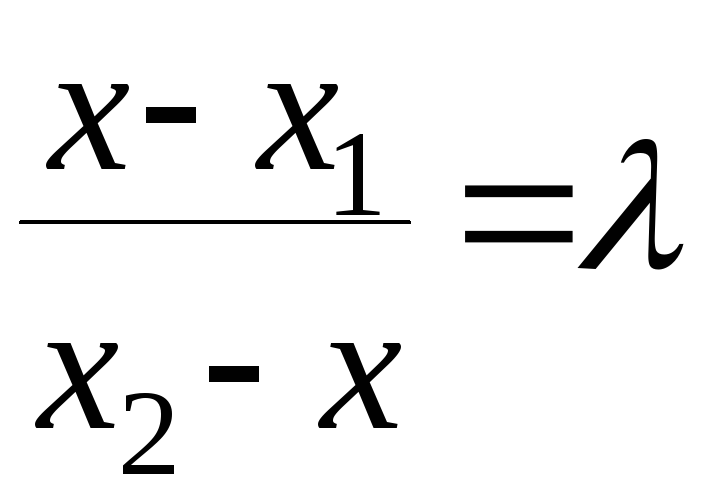 .
Преобразуя последнее выражение, получим:
.
Преобразуя последнее выражение, получим:
![]() .
.
Найдем из последнего равенства х:
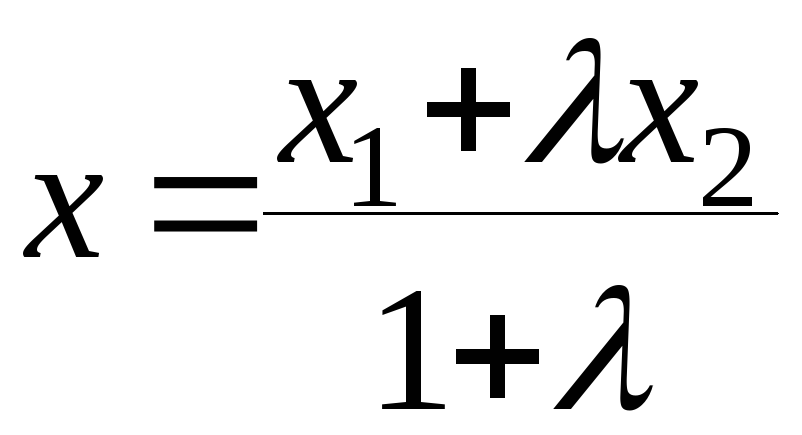 .
.
По той же теореме о пропорциональности длин отрезков находим y:
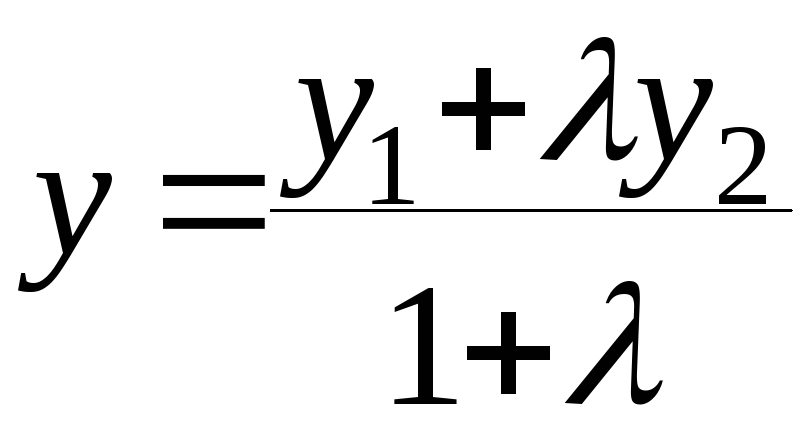 .
.
Если отрезок задан в пространстве, то координата z равна:
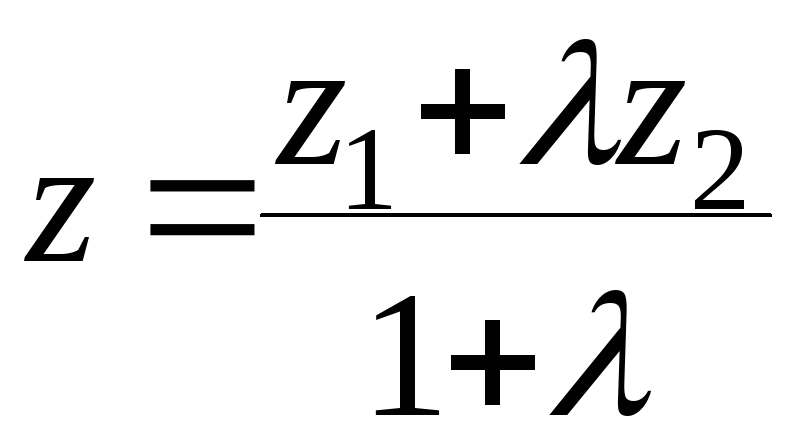 .
.
Таким
образом, координаты точки, делящей
отрезок в заданном отношении
![]() равны:
равны:
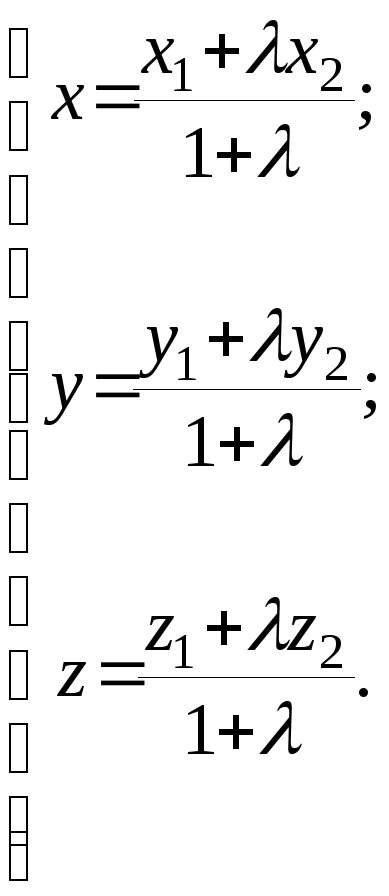 (1.3)
(1.3)
Если
точка М
делит отрезок
![]() пополам,
т.е.
пополам,
т.е.
![]() ,
а значит,
,
а значит,
![]() ,
формулы (1.3) примут вид:
,
формулы (1.3) примут вид:
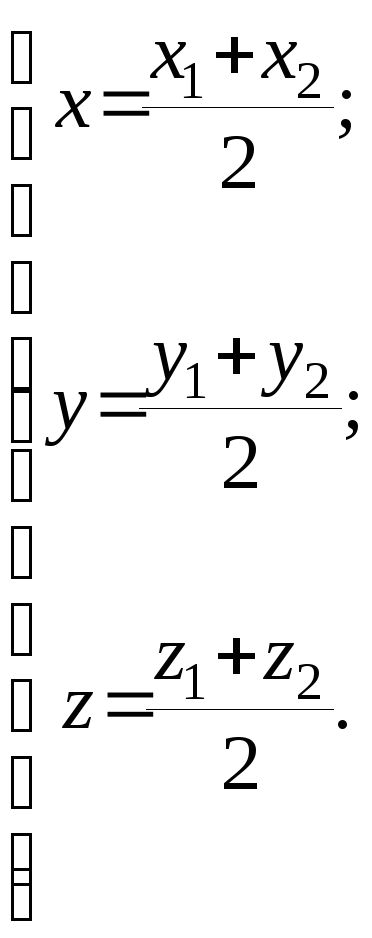 (1.4)
(1.4)
Следовательно:
Координаты точки, делящей отрезок пополам, равны полу суммам соответственных координат концов этого отрезка.
1.6 Полярная и цилиндрическая системы координат
1. Полярная система координат.
Рассмотрим
декартову прямоугольную систему
координат на плоскости. Полярным
лучом называется
подвижный
луч, начало которого совпадает с началом
координат, т.е. с точкой О(0;
0), а
направление совпадает с положительным
направлением оси Ох.
Можно считать, что начальное
положение
полярного луча - это положительная
полуось Ох.
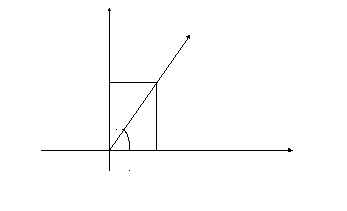
Возьмем на плоскости произвольную точку
М(х;
у). Повернем
полярный луч до совпадения с этой точкой,
угол образованный при этом полярным
лучом с положительным направлением
оси Ох,
обозначим:
![]() ,
а расстояние точкиМ(х;
у)
от начала координат обозначим:
,
а расстояние точкиМ(х;
у)
от начала координат обозначим:
![]() .
.
![]()
![]()
![]() М(х;
у)
М(х;
у)
![]()
![]()
![]()
![]() х
х
![]()
Полярный луч и угол его поворота образуют полярную систему координат на плоскости.
Упорядоченная
пара чисел
![]() называетсяполярными
координатами
точки М.
называетсяполярными
координатами
точки М.
Таким
образом, в полярных координатах запишем:
![]() .
.
Из рисунка очевидна связь между декартовыми и полярными координатами:
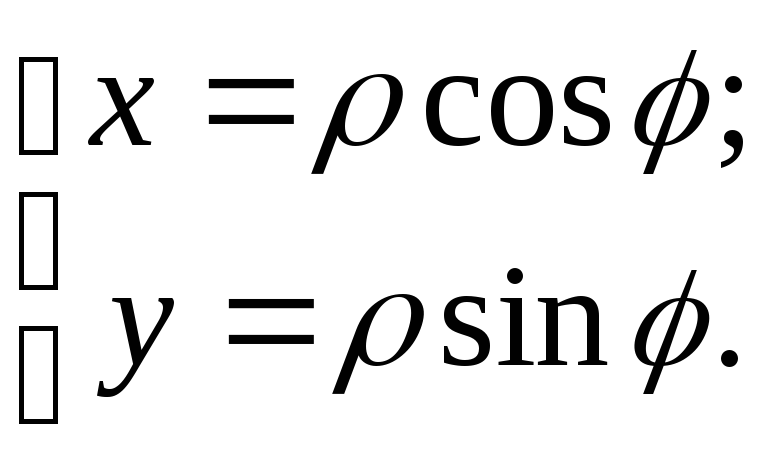 (1.5)
(1.5)
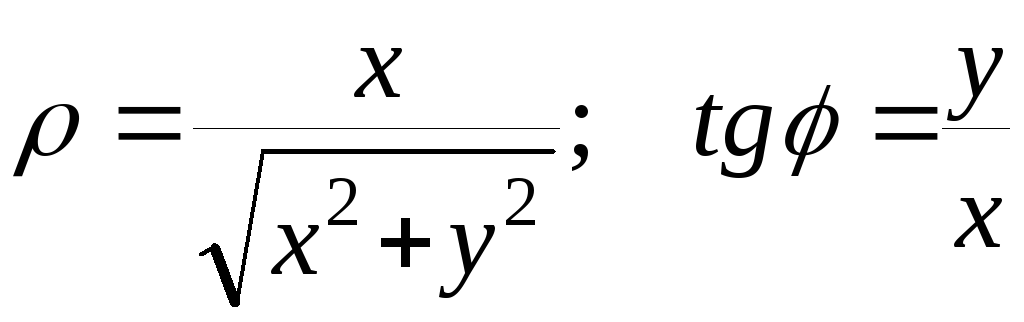 (1.6)
(1.6)
Пример.
Найти
полярное уравнение окружности с центром
в начале координат, радиусом
![]() .
.
Решение.
Уравнение заданной окружности:
![]() .
.
Применяя формулу (1.5), получим:
![]()
![]()
Таким
образом, полярное уравнение окружности:
![]()
1. Цилиндрические координаты точки в пространстве.
Цилиндрическими
координатами точки М
в пространстве называется упорядоченная
тройка чисел:
![]() ,
при этом:
,
при этом:
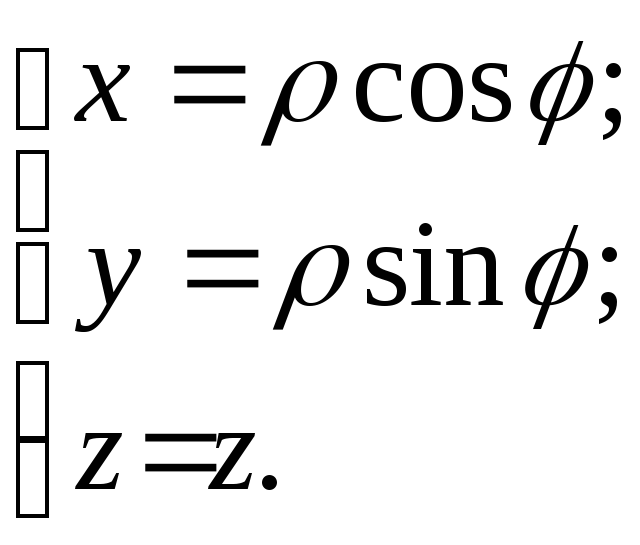 (1.7)
(1.7)
ЛЕКЦИЯ 2
ВЕКТОРЫ. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
2.1 Понятие вектора
Вектор − это направленный отрезок прямой, имеющий начало (обозначается точкой) и конец (обозначается стрелкой).
 А
.
В
А
.
В
![]()
Изображенный
на рисунке вектор можно записать, как
вектор
![]() ,
либо как вектор
,
либо как вектор
![]() .
.
При этом А – начало вектора, В – конец вектора.
Длиной (или модулем) вектора называется расстояние между его началом и концом.
Математические векторы свободно перемещаются в пространстве, не изменяя своей длины и направления, посредством параллельного переноса.
Коллинеарными называются векторы, которые могут быть сведены на одну прямую линию. Коллинеарные векторы, направленные в одну и ту же сторону, называются сонаправленными.
Векторы равны, если:
они имеют одинаковые длины;
они являются коллинеарными и сонаправленными.
Коллинеарные векторы с одинаковыми длинами, но направленные в противоположные стороны, имеют разные знаки.
![]()
![]()
![]()
На рисунке:
![]() .
.
Следовательно:
![]()
Единичным
вектором вектора
![]() называется вектор
называется вектор
![]() ,
такой, что:
,
такой, что:
![]() .
.
![]()
1
![]()
Ноль-вектором называется вектор, имеющий длину, равную нулю. Ноль-вектор имеет произвольное направление в пространстве.
Линейные операции над векторами.
1. Умножение вектора на число
Произведением
вектора
![]() на
число
на
число
![]() является вектор
является вектор![]() ,
такой, что выполняется:
,
такой, что выполняется:
1)
![]()
2)
![]() при
при![]() ;
;
![]() при
при
![]() .
.
Сложение векторов
Правило треугольника
Чтобы найти сумму двух векторов, надо начало одного совместить с концом другого,
тогда результатом сложения является вектор, имеющий начало, совпадающее с началом первого вектора, а конец, совпадающий с концом второго.

![]()
![]()
![]()
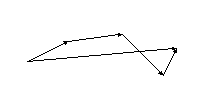
С помощью правила треугольника можно находить сумму любого конечного числа векторов, совмещая начало следующего слагаемого вектора с концом предыдущего. Суммой является вектор, начало которого совпадает с началом первого слагаемого, а конец с концом последнего.

![]()
![]()
![]()
![]()
![]()
![]()
![]()
Правило параллелограмма
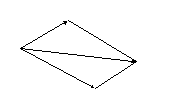
Чтобы найти сумму двух векторов, надо совместить начало одного из слагаемых векторов с началом другого, и построить параллелограмм на этих векторах, как на сторонах. Суммой является вектор, совпадающий с диагональю построенного параллелограмма, имеющий начало, совпадающее с общим началом слагаемых векторов, а конец – в противоположном углу параллелограмма.
![]()
![]()
![]()
![]()
ЛЕКЦИЯ 3
КООРДИНАТЫ ВЕКТОРА
3.1 Определение координат вектора
Рассмотрим декартову прямоугольную систему координат на плоскости. На осях координат выберем единичные векторы:
![]()
Очевидно,
что
![]() .
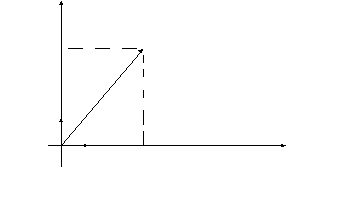
Рассмотрим произвольный вектор
.
Рассмотрим произвольный вектор
![]() ,совместив
его начало с началом координат. Опустим
перпендикуляры из конца этого вектора
на координатные оси. Полученные проекции
обозначим соответственно
,совместив
его начало с началом координат. Опустим
перпендикуляры из конца этого вектора
на координатные оси. Полученные проекции
обозначим соответственно
![]() .
Согласно правилам умножения вектора
на число и сложения векторов, можем
записать:
.
Согласно правилам умножения вектора
на число и сложения векторов, можем
записать:
![]() (3.1)
(3.1)
y
![]()
![]()
![]()
O
![]()
![]() X
X
Числа
![]() называются координатами вектора
называются координатами вектора
![]() .
Тот факт, что
.
Тот факт, что
![]() - координаты вектора
- координаты вектора
![]() принято
записывать так:
принято
записывать так:
![]() ={
={![]() }.
При этом, векторы
}.
При этом, векторы![]() называются единичнымиортами.
называются единичнымиортами.
Рассмотрим
на плоскости две точки А(![]() )
иВ(
)
иВ(![]() ).
Тогда координатами вектора
).
Тогда координатами вектора![]() являются разности соответственных
координат конца и начала этого вектора,
т.е.
являются разности соответственных
координат конца и начала этого вектора,
т.е.![]() =
=![]() .
.
Рассмотрим
теперь декартову прямоугольную систему
координат в пространстве. Третьей ортой
при этом является вектор:
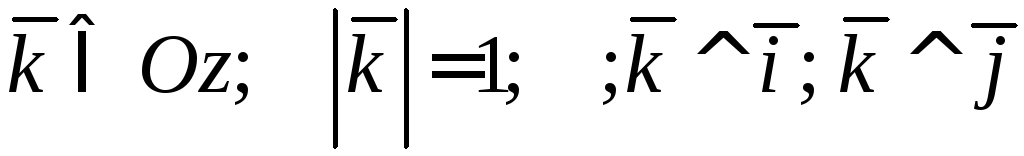 .
Следовательно, в пространстве:
.
Следовательно, в пространстве:
![]() .
(3.2)
.
(3.2)
Аналогично, в пространстве координаты векторов:
![]() ={
={![]() }.
}.
![]() =
=![]() .
.
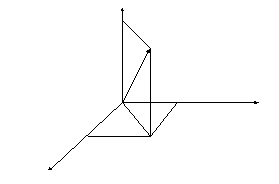 z
z
![]()
![]()
![]()
o y
![]()
x
Линейные операции над векторами в координатной форме
Рассмотрим
векторы
![]() и
и![]() .
Найдем вектор
.
Найдем вектор![]() .
.
Координаты этого вектора равны суммам соответственных координат заданных векторов, т.е.
![]() .
(3.3)
.
(3.3)
При
умножении векторов
![]() и
и![]() на скаляры (числа)
на скаляры (числа)![]() соответственно получим следующие
выражения:
соответственно получим следующие
выражения:
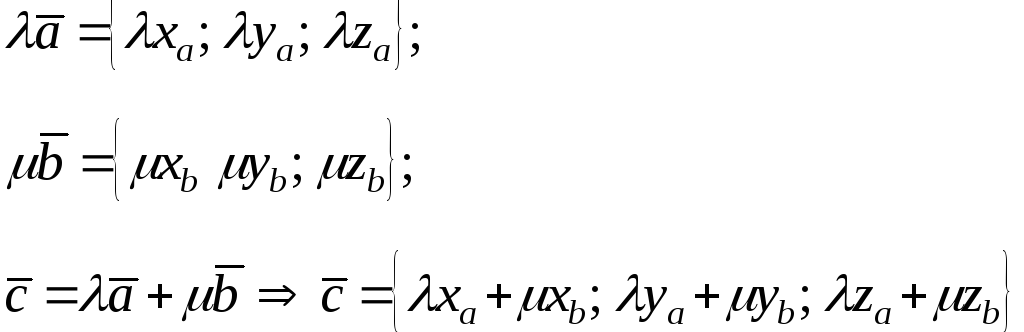
Свойства линейных операций над векторами

3.3 Длина вектора в координатной форме
Длина вектора равна квадратному корню из суммы квадратов его координат
На
плоскости:
![]() .
(3.4)
.
(3.4)
В
пространстве:
![]() .
(3.5)
.
(3.5)
ЛЕКЦИЯ 4
СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
4.1 Определение скалярного произведения
Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними
При этом углом между векторами является наименьший, если двигаться против часовой стрелки, образуемый этими векторами угол.
Обозначения:
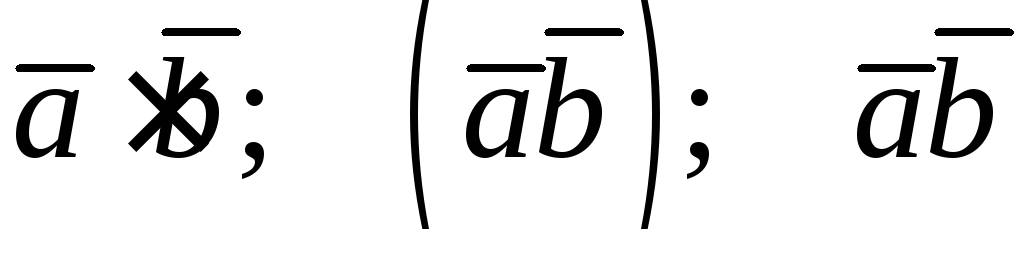
Таким образом, по определению запишем формулу:
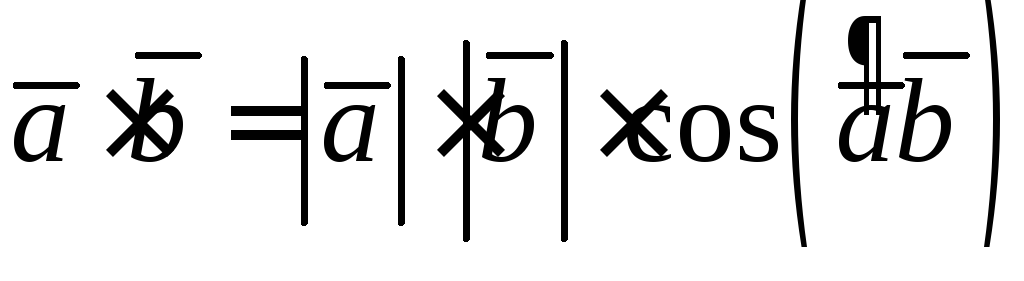 .
(4.1)
.
(4.1)
Свойства скалярного произведения
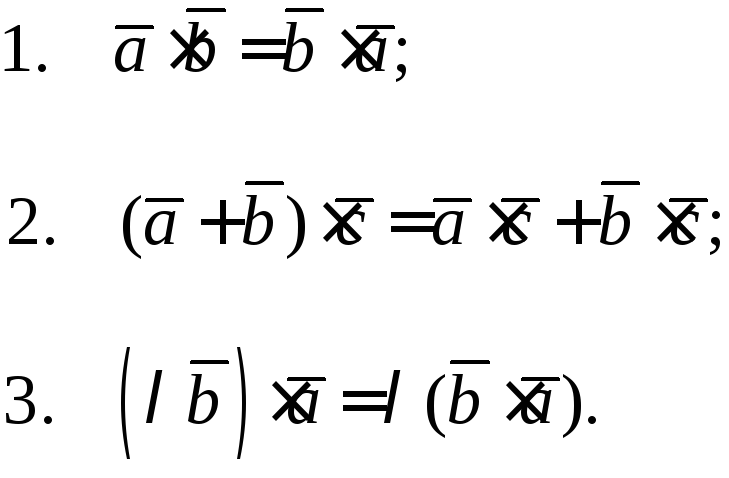
Скалярный квадрат вектора
Из определения скалярного произведения следует:
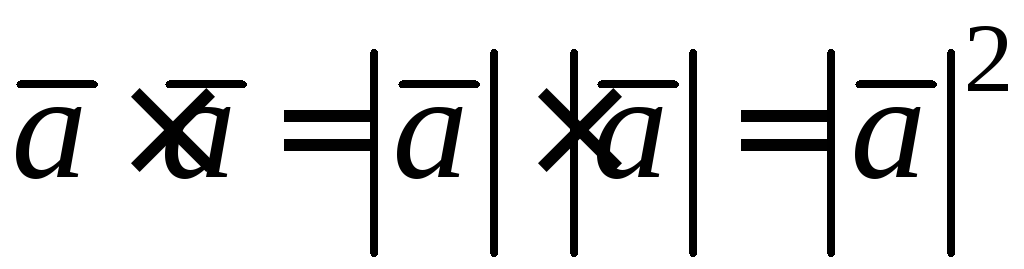 .
.
Т.е., скалярный квадрат вектора равен квадрату длины этого вектора.
Как
правило, скалярный квадрат вектора,
т.е. скалярное произведение вектора на
себя, обозначается так:
![]() .
Следовательно, можем записать формулу:
.
Следовательно, можем записать формулу:
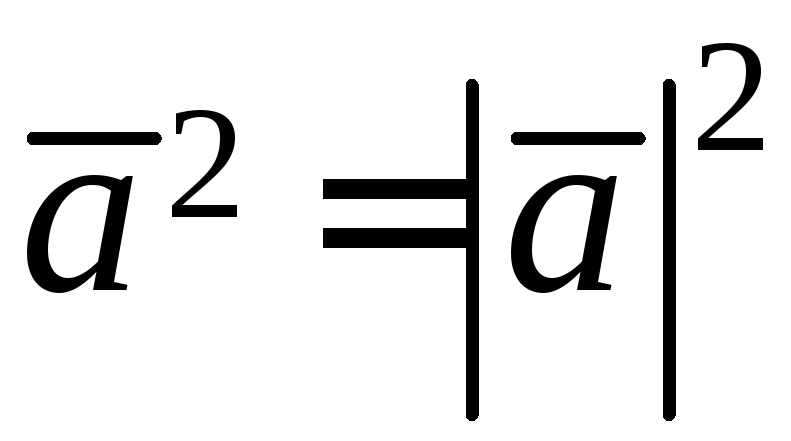 (4.2)
(4.2)
Из формулы (4.2) следует еще одна важная формула:
 (4.3)
(4.3)
Модуль вектора равен квадратному корню из скалярного квадрата этого вектора.
Скалярное произведение векторов в координатной форме
Из определения скалярного произведения и свойств единичных орт следует:
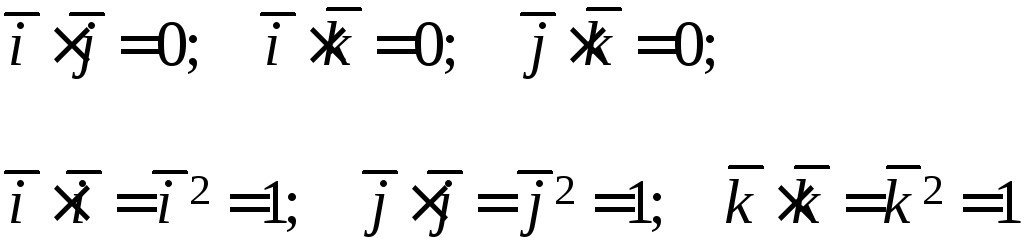 (4.4)
(4.4)
Пусть
нам заданы векторы:
![]() и
и![]() .
.
Из формул (3.2) и (4.4) следует формула для вычисления скалярного произведения векторов в координатной форме:
![]() (4.5)
(4.5)
Таким образом, скалярное произведение векторов равно сумме произведений соответственных координат этих векторов.
