
Вопрос №1Электрическая цепь постоянного тока
Электрической цепью называют совокупность соединенных друг с другом источников электрической энергии и потребителей, по которым может протекать электрический ток. Графическое изображение электрической цепи с применением соответствующих условных обозначений называютэлектрической схемой.
Реальная
электрическая схема обычно содержит
все элементы, включенные в схему и
отражающие данные о том, что они в
действительности собой представляют.
Например, на рис. 1.1,априведена
упрощенная реальная схема питания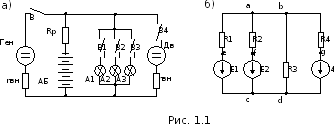
Зависимость тока, протекающего по элементу электрической схемы, от напряжения на ней называется вольт-амперной характеристикой(в.а.х.).
Сопротивления, в.а.х. которых представляет
собой прямую линию, проходящую через
начало координат, называют линейными(рис. 1.2,а). В противном случае
сопротивлениенелинейно. На
рис. 1.2,б в качестве примера в.а.х.
нелинейного элемента приведена в.а.х.
полупроводникового диода. Электрическая
схема, содержащая только линейные
элементы является линейной. В случае,
если схема содержит хотя бы один
нелинейный элемент, ее называют
нелинейной. Строго говоря, абсолютно
линейные элементы встречаются в практике
редко. Однако, если степень нелинейности
в.а.х. невелика, то такой элемент
приближенно можно считать линейным.
Источники
электрической энергии также характеризуются
вольтамперными характеристиками,
однако, в отличие от в.а.х. сопротивлений
(пассивных элементов электрической
цепи) они не проходят через начало
координат. В качестве примера на рис.3,а
приведена в.а.х. реального источника
энергии. Она обычно характеризуется
двумя точками - точкой холостого хода
(А), когда ток источника равен нулю, и
точкой короткого замыкания (B),
когда источник закорочен и напряжение
на его зажимах равно нулю. Между этими
точками в.а.х. источника обычно в той
или иной степени нелинейна. Однако,
обычно источники энергии эксплуатируют
в режимах далеких от режима короткого
замыкания, на участке АС в.а.х. Участок
близок к прямой линии. Поэтому рабочий
участок в.а.х. можно приближенно считать
линейным (рис. 1.3,б). Это дает возможность
в расчетной схеме заменить реальный
источник электрической энергии
идеализированным источником ЭДСЕи некоторым внутренним сопротивлением
источникаrвн
(рис.3,в).
Нетрудно убедиться в том, что в.а.х. источника ЭДС представляет собой прямую вертикальную линию (рис. 1.3,г), а в.а.х. всей схемы (рис. 1.3,в) представляет собой разность в.а.х. источника ЭДС и в.а.х. линейного сопротивления (см. рис. 1.2,а). В результате получается в.а.х., изображенная наклонной линией на рис. 1.3,г, которая совпадает с в.а.х. рис. 1.3,б. Именно так и было сделано при переходе от реальной к расчетной схеме на рис. 1.1.Для удобства анализа и расчета электрические схемы обычно мысленно разделяют на отдельные части, к которым непосредственно могут быть применены те или иные законы электротехники. Рассмотрим схему рис.1,б. Точкиа, b, c, dявляются точками, где сходятся три проводника. Такие точки схемы, где сходятся три и болееветви, называютузлами.Ветвьюназывают неразветвленный участок схемы, соединяющий два узла. Ветвь обычно содержит сопротивление (ветвьb – d) или сопротивление и источник электрической энергии (например, ветвь c – e – a). Узлы схемы, обязательно обозначаются четко выделенной точкой, которая показывает, что здесь проводники соединяются. При отсутствии точки предполагается, что в этом месте проводники пересекаются, но не соединяются.Замкнутым контуромсхемы называют такую ее часть, состоящую из двух или более ветвей, в которой ветви соединены друг с другом так, что конец первой ветви соединен с началом второй ветви, конец второй ветви соединен с началом третьей и т.д., а конец последней (n-ой) ветви соединен с началом первой ветви. На схеме рис. 1.1,бможно, например выделить замкнутые контуры:a – c – e – a,a – f – c – d – b – a,a – b – g – d – c – e – aи др.
Постоянным токомназывается ток, неизменный во времени по величине. Он создается направленным упорядоченным движением электрических зарядов под воздействием электрического поля. При этом в качестве положительного направления тока принимается направление движения положительных зарядов.
Сила тока — количество электричестваq, протекающего через поперечное сечение проводника в единицу времени:
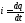 . (1.1)
. (1.1)
Отсюда следует соотношение:
 (1.2)
(1.2)
Сила тока - величина скалярная (не векторная), однако, как указывалось, ей приписывают определенное направление (знак). Обычно буквой iобозначают силу тока в данный момент времени. Так как постоянный ток во времени не меняется, его обозначаютI.
Плотность тока— отношение силы тока к площади поперечного сечения проводникаS, через который этот ток протекает:
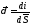 . (1.3)
. (1.3)
Отсюда следует:
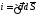 . (1.3-а)
. (1.3-а)
Если ток распределен равномерно по сечению проводника:
 . (1.4)
. (1.4)
Сила тока измеряется в амперах (А), либо производных единицах, например: 1 мА = 10-3А,
1 кА = 103А и других.
Линией токаназывают линии, представляющие траектории движения зарядов в электрическом поле.
Часть пространства, ограниченная линиями тока, называется трубкой тока. Она характерна тем, что в любом ее сечении сила тока одинакова.
Вопрос №2 Законы электрических цепей
Первый закон кирхгофа
Рассмотрим тело произвольной формы,
ограниченное поверхностью S(рис. 1.4,а)
Линии тока входят в это тело и выходят из него. Если какая-то линия входит в тело, но не выходит, то внутри тела накапливаются заряды. Но бесконечно долго это продолжаться не может, так как ограничивается емкостью тела. Поэтому можно считать, что число линий тока, входящих в тело и выходящих из него равны между собой. Если считать вход линии тока в тело положительным пересечением, а выход - отрицательным, то можно записать:
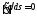 . (1.5)
. (1.5)
Приведенное соотношение носит название принципнепрерывности линий тока.
Используем полученное соотношение для узласхемы. Охватим этот узел замкнутой поверхностью (рис.4,б). Так как токи подходят к узлу и отходят от него только по проводникам, выражение (1.5) примет вид:
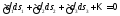 . (1.6)
. (1.6)
Или:
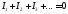 . (1.7)
. (1.7)
В более компактном виде:
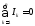 .
.
Это и есть математическая запись по 1-у закону Кирхгофа.
Таким образом, алгебраическая сумма токов, подтекающих к любому узлу схемы равна нулю. Или, иначе, сумма подходящих к узлу токов равна сумме выходящих из узла токов.
Отсюда следует, что если схема на каком-либо участке не разветвляется, то и ток, в любом сечении этого участка будет один и тот же. В частности, в каждой точке ветвисхемы ток будет иметь одно и тоже значение.
Второй закон Кирхгофа
Рассмотрим часть сложной схемы, образующую замкнутый контур (рис.1.5,б). Обозначим потенциалы узлов1,2,3… Задав произвольно направления токов в ветвях, запишем соотношения, связывающие потенциалы двух соседних узлов 1 и 2:
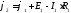 . (1.12)
. (1.12)
Здесь Е1 – величина источника ЭДС данной ветви;
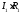 –
падение напряжения, создаваемое током
ветвиI1на
сопротивлении ветвиR1.
–
падение напряжения, создаваемое током
ветвиI1на
сопротивлении ветвиR1.
В каждом конкретном случае каждое из этих слагаемых может быть положительным или отрицательным, в зависимости от направления тока и ЭДС.
Если записать аналогичные соотношения для всех других ветвей, образующих замкнутый контур, получим:
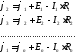 . (1.13)
. (1.13)
Сложим полученные соотношения:
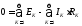 или
или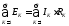 (1.14)
(1.14)
Таким образом, в любом замкнутом контуре алгебраическая сумма ЭДС равна алгебраической сумме падений напряжения.
Закон Ома (для участка электрической цепи)
Рассмотрим участок трубки тока сечением
dSдлинойdl,
по которой протекает токdi(рис. 1.5,а). Так как заряды движутся,
на них действует сила ,
где напряженность поля
,
где напряженность поля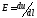 .
Под действием этой силы скорость движения
зарядовυ в
идеальном случае должна была бы все
время возрастать, однако из-за хаотичного
(теплового) движения частиц материала,
препятствующего движению зарядов,
устанавливается некоторая средняя
скорость
.
Под действием этой силы скорость движения
зарядовυ в
идеальном случае должна была бы все
время возрастать, однако из-за хаотичного
(теплового) движения частиц материала,
препятствующего движению зарядов,
устанавливается некоторая средняя
скорость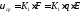 .
Количество зарядов в единицу времени
.
Количество зарядов в единицу времени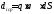 .
Тогда плотность тока
.
Тогда плотность тока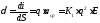 ,
здесь величина
,
здесь величина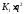 зависит только от свойств материала.
Обозначим
зависит только от свойств материала.
Обозначим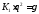 .
.
Тогда:
 . (1.8)
. (1.8)
Полученное соотношение (1.8) называется
законом Ома в дифференциальной форме.
Для простых практических случаев это
соотношение целесообразно преобразовать.
Подставив в (1.8) значение Е, получим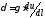 ,
откуда
,
откуда .
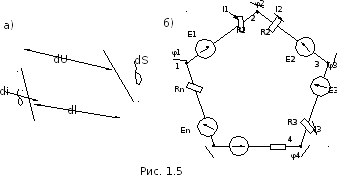
После интегрирования получим
.
После интегрирования получим .
.
Умножив
и разделив правую часть на S,
получим ,
где
,
где
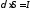 в соответствии с (1.4).
в соответствии с (1.4).
Величина носит
названиеудельная проводимость
материалапроводника. Величина,
обратная ей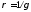 называетсяудельное сопротивлениепроводника. Обозначим:
называетсяудельное сопротивлениепроводника. Обозначим:
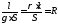 — сопротивление проводника. (1.9)
— сопротивление проводника. (1.9)
Теперь окончательно получим:
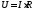 . (1.10)
. (1.10)
Таким образом доказано, что напряжение на зажимах проводника Uравно произведению силы протекающего через проводник тока на сопротивление проводника.
Из (1.10) следует:
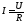 .
.
Иногда для удобства записи и практических расчетов вводят величину, обратную R:
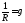 — проводимость проводника.
— проводимость проводника.
Тогда получим другую форму записи закона Ома:
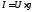 . (1.11)
. (1.11)
Напряжение Uизмеряют в вольтах (В) или в производных единицах:
1 мВ = 10-3В
1 кВ = 103В и других.
Сопротивление проводника Rизмеряется в Омах (Ом) или производных единицах:
1 кОм = 103Ом
1 МОм = 106 Ом и других.
Проводимость gизмеряется в сименсах (См): 1См= 1/Ом
Закон Джоуля – Ленца
Если за время dtчерез поперечное сечение проводника
пройдет некоторое количество электричества,
то работа по перемещению этого количества
электричества: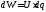 .
.
Потребляемая при этом мощность:
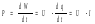
Используя формулу закона Ома (1.10) можно записать полученное выражение закона Джоуля – Ленца в следующих формах:
 ;
; ;
; (1.15)
(1.15)
Или, через проводимость:
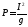 ;
; .
(1.16)
.
(1.16)
Иногда приведенные варианты формул могут создать иллюзию противоречия о влиянии величины сопротивления Rна мощностьP. Однако, необходимо учитывать, что рассматривать изолированно изменениеR нельзя, так как при измененииPсоответственно изменяется либо ток, либо напряжение, либо обе эти величины.
Величина мощности Ризмеряется в ваттах: Вт = ВА, либо в производных единицах (киловаттах, мегаваттах, милливаттах и т.д. ).
Вопрос №3 Метод непосредственного применения законов Кирхгофа
Метод уравнений Кирхгофа
Применение этого метода рассмотрим на
примере схемы рис.1.10,а. Метод основан
на непосредственном применении для
расчета схемы уравнений по 1-му и 2-му
законам Кирхгофа. Необходимое число
уравнений равно числу неизвестных токов
в ветвях. В данном случае неизвестных
токов три, следовательно необходимо
составить систему из трех уравнений.
Для составления уравнений необходимо
предварительно задаться направлением
токов в ветвях. Так как эти токи пока
неизвестны ни по величине, ни по
направлению, принимаем направление эти
токов произвольно. В случае, если
какие-либо токи ошибочно направлены не
так, как они протекают, соответствующий
результат получится с отрицательным
знаком. При этом никаких новых расчетов
не производится, а просто изменяют
направление тока на правильное.
При составлении уравнений обычно вначале составляют наибольшее возможное число уравнений первому закону Кирхгофа, т.к. эти уравнения более просты. Однако здесь надо следить за тем, чтобы эти уравнения были независимы, т.е. не являлись следствием или повторением предыдущих, уже записанных уравнений. Например, в схеме рис. 1.10,адва узла, однако может быть записано только одно уравнение, в чем легко убедиться, записав уравнения для узловаиб. В общем случае для схемы, имеющейyузлов можно записатьy-1 уравнений по 1-у з. Кирхгофа. Например, для схемы рис.1.10,б, имеющей четыре узла, может быть записано три уравнения по первому закону Кирхгофа. Недостающие уравнения записываем по второму закону Кирхгофа. При этом следует предварительно выбрать контуры, для которых будем составлять эти уравнения. Здесь также следует следить за тем, чтобы эти уравнения были независимы. Практически для этого достаточно, чтобы в каждое следующее уравнение входила хотя бы одна новая ветвь, не входившая в предыдущие. В схеме рис.10,а можно выделить три замкнутых контура:adbca, bdaebиbcaeb, однако только два из уравнений для этих контуров будут независимыми. Составим, например, уравнения по 2-у закону Кирхгофа для контуровadbcaиbdaeb. При составлении уравнений безразлично, обходить ли замкнутый контур по часовой стрелке или против, т.к. это приведет лишь к изменению всех знаков в уравнении на обратные. Тогда полная система уравнений для расчета схемы рис. 1.10,а:
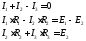 (1.27)
(1.27)
В результате решения этой системы находим искомые точки I1,I2,I3. Решение может быть выполнено любым известным методом.
Оценивая данный метод отметим, что даже для такой простой схемы, как схема рис. 1.10,априходится решать систему из трех уравнений. Для более сложных схем задача резко усложняется. Например, для схемы рис. 1.10,бполучим систему из 6 уравнений. Поэтому областью применения метода уравнений Кирхгофа является расчет не очень сложных схем. При ручном счете без применения ЭВМ таким методом обычно рассчитывают схемы, описываемые системой не более, чем из трех уравнений.
Вопрос №4 Метод контурных токов
В основе этого метода также лежит принцип замены переменных. Здесь вместо искомых токов в ветвях будем определять потенциалы узловых точек схемы. Зная их, можно используя потенциальные соотношения, аналогичные (1.13), найти токи в ветвях.
Предварительно отметим, что любую точку электрической схемы можно заземлить, если ранее ни одна другая точка с другим потенциалом не была заземлена. Заземление какой-либо точки схемы свидетельствует лишь о том, что потенциал этой точки принят равным нулю. Распределение токов в схеме при этом не изменится, так как не возникает никаких новых ветвей и цепей для протекания тока. Нельзя, однако, заземлять одновременно две или более точек, если они имеют разные потенциалы, так как в этом случае образуются дополнительные ветви и схема, в сущности становится другой.
Воспользовавшись приведенными соображениями, заземлим, например, узловую точку dсхемы рис. 1.10,б. Тем самым потенциал этой точки стал известен (равен нулю). Следовательно для расчета этой схемы методом узловых потенциалов достаточно определить только потенциалы остальных узловa,b,c. Практически в сложных схемах выгоднее заземлять тот узел, где сходится больше всего ветвей. Составим для узловa,b,cуравнения по 1-у закону Кирхгофа:
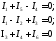 (1.37)
(1.37)
Метод контурных токов
Рассмотрим схему рис.1.10,б. Полагаем, что в каждом независимом контуре течет свой контурный ток, который и подлежит определению в результате расчета. По существу, здесь мы производим замену переменных, т.е. вместо неизвестных токов в ветвях определяем контурные токи. Эти токи являются фиктивными расчетными величинами. Смысл такой замены в том, чтобы сократить число уравнений и, соответственно, упростить расчет. Контуры, в которых будем определять контурные токи, выбираем так, чтобы они охватывали все ветви схемы. Для схемы рис. 1.10,б необходимо определить 6 токов в ветвях, т.е. по методу уравнений Кирхгофа пришлось бы составить и решить систему из 6 уравнений. Вместе с тем независимых контуров, охватывающих все ветви схемы, здесь всего три. Между контурными токами и токами в ветвях существуют простые логические соотношения. Например, ток ветви I1 и контурный ток I11 равны между собой. Ток ветви I2 равен сумме контурных токов I11 и I22 и т.д. Таким образом, зная контурные токи всегда легко определить токи в ветвях:
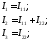
 (1.28)
(1.28)
Для получения контурного уравнения для 1-го контура воспользуемся 2-м законом Кирхгофа:
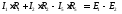
Подставив сюда контурные токи, получим:
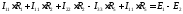 ,
,
или
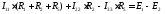 (1.29)
(1.29)
Введем обозначения:
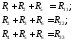 (1.30)
(1.30)
Величины R11, R22, R33называемсобственнымиконтурными сопротивлениями. Они всегда представляют собой сумму всех сопротивлений, входящих в данный контур.
Сопротивления, входящие одновременно в два контура, назовем взаимными контурными сопротивлениями. Их знак положителен, если в смежной ветви контурные токи совпадают по направлению и отрицателен — если не совпадают:
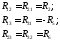 (1.31)
(1.31)
И, наконец, алгебраическую сумму всех ЭДС, входящих в контур, назовем контурной ЭДС, причем их знак будем считать положительным, если направление ЭДС совпадает с произвольно принятым направлением контурного тока и отрицательным,— если не совпадает:
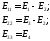 (1.32)
(1.32)
Подставив введенные обозначения в уравнение (1.29) и проделав аналогичные преобразования для двух других контуров, получим окончательно систему уравнений для расчета схемы методом контурных токов:
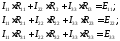 (1.33)
(1.33)
Таким образом, уравнения по методу контурных токов элементарно просты, всегда однотипны и составляются по очень простому правилу. По существу, систему уравнений по методу контурных токов (1.33) можно записать сразу после, того как определено число независимых контуров (число контурных токов). Затем для данной конкретной схемы определяют собственные (1.30) и взаимные (1.31) сопротивления, а также контурные ЭДС (1.32). Подставив все эти величины в систему уравнений (1.33) и решив ее, найдем все контурные токи. Далее по соотношениям (1.28) нетрудно найти искомые токи в ветвях.
Решение системы (1.33) удобнее всего вести с помощью определителей:
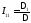 ;
; ;
;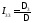 (1.34)
(1.34)
где
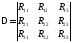 – определитель системы (1.35)
– определитель системы (1.35)
Важно отметить, что этот определитель симметричен относительно главной диагонали, т.к. взаимные сопротивления попарно одинаковы (см. (1.31)).
Определители D1,D2,D3получим, заменив в определителеDсоответственно 1-й,2-й,3-й столбец столбцом свободных членов (контурных ЭДС). Например:
 (1.36)
(1.36)
Метод контурных токов — мощный расчетный метод, широко применяемый в практике для расчета сложных схем. Его используют и при расчетах на ЭВМ, при этом систему уравнений (1.33) записывают в матричной форме, а при расчетах используют стандартные подпрограммы операций с матрицами.
Особенно выгодным является использование метода контурных токов для расчета сложных схем с большим числом ветвей, но малым числом независимых контуров.
Вопрос №5 Метод узлового напряжения
Данный метод является частным случаем рассмотренного выше метода узловых потенциалов. В отличии от него предлагаемый метод применим только для схем любой степени сложности с двумя узловыми точками. Поэтому его иногда называют ”метод двух узлов”. Для двухузловых схем число уравнений по методу узловых потенциалов равно у –1 = 1, т.е. система уравнений (1.42) превращается лишь в одно уравнение, т.к. второй узел можно заземлить. Рассмотрим схему рис. 1.11. Для этой схемы от системы (1.43) останется только первое уравнение, причем в левой его части останется лишь одно слагаемое:
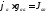 (1.44)
(1.44)
где
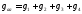 – сумма проводимостей всех ветвей схемы
(рис.11)
– сумма проводимостей всех ветвей схемы
(рис.11)
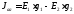 —
узловой ток равный сумме произведений
ЭДС ветвей на проводимости этих ветвей
с учетом знака, определяемого направлением
источников ЭДС ( к узлуа:плюс, от
узлаа: минус). Тогда потенциал узлаа(он же является напряжением между
точкамиаиb):
—
узловой ток равный сумме произведений
ЭДС ветвей на проводимости этих ветвей
с учетом знака, определяемого направлением
источников ЭДС ( к узлуа:плюс, от
узлаа: минус). Тогда потенциал узлаа(он же является напряжением между
точкамиаиb):
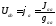 или
или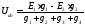 (1.45)
(1.45)
В общем случае для двухузловой схемы с любым числом ветвей n:
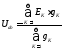 (1.46)
(1.46)
После определения узлового напряжения схемы рис. 1.11 легко по соотношениям, аналогичным (1.38) найти токи в ветвях с учетом условно принятых направлений токов:
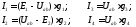 (1.47)
(1.47)
Таким образом, схема рис.11. рассчитана без составления и решения какой-либо системы уравнений.
Отметим, что для расчета этой схемы по методу уравнений Кирхгофа потребовалась бы система из 4 уравнений, а по методу контурных токов из 3 уравнений. Отсюда видно, что правильный выбор метода расчета для заданной конкретной схемы может резко упростить решение задачи.
Вопрос № 6 Теорема об эквивалентном генераторе
Предварительно рассмотрим представление электрической схемы в виде двухполюсника. В любой электрической цепи можно выделить какую-либо одну ветвь, а всю остальную часть схемы не изображать, а обозначить прямоугольником с двумя выводами, к которым и подключена выделенная ветвь (рис.1.15,а). Внутри прямоугольника предполагается любая сколь угодно сложная схема. Если в ней имеются источники энергии, то такой двухполюсник называется активным и обозначается буквойА, в противном случае буквойП.
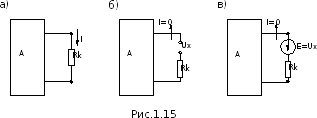
Рассмотрим теперь следующее свойство
электрических цепей. Разомкнем ветвь
с сопротивлением Rк(рис. 1.15,б). Очевидно, при этом ток в
ветви станет равен нулю, а напряжение
в точке разрыва будет равно некоторой
величинеUх,
которое называем напряжение холостого
хода. Такого же эффекта можно добиться
и другим путем — включив в эту ветвь
источник ЭДСЕ, величина которого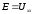 Конечно,
токи в остальных ветвях схемы (внутри
двухполюсника) при этом тоже изменятся.
Конечно,
токи в остальных ветвях схемы (внутри
двухполюсника) при этом тоже изменятся.
Теорема об эквивалентном генераторе позволяет определить ток в выделенной ветви с сопротивлением Rк, не рассчитывая остальные токи (и всю схему в целом).
В исходной схеме (рис. 1.16,а) включим в ветвь с сопротивлениемRкдва одинаковых идеализированных источника ЭДСЕ1иЕ2 (рис. 1.16,б). Так как они включены встречно, их сумма равна нулю и поэтому они не окажут влияние на величину токаI в ветви и в других ветвях схемы.

Величина источников Е1иЕ2может быть любой, лишь бы они были равны
между собой. Выберем величиныЕ1иЕ2таким образом, чтобы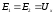 .Далее
применим к расчету этой схемы метод
наложения. На первом этапе оставим в
схеме источникЕ1 и все
источники внутри активного двухполюсника
(рис. 1.16,в). Так какЕ1 =Uх, то ток
ветви в этой схемеI’=0.
На втором этапе оставим источникЕ2,
а исключим источникЕ1 и
все источники внутри двухполюсника
(двухполюсник при этом станет пассивным).
Так как источникЕ2в схеме
(рис. 1.16,г) является единственным и
включен он в ветвь, где надо определить
ток, величина этого тока может быть
легко определена:
.Далее
применим к расчету этой схемы метод
наложения. На первом этапе оставим в
схеме источникЕ1 и все
источники внутри активного двухполюсника
(рис. 1.16,в). Так какЕ1 =Uх, то ток
ветви в этой схемеI’=0.
На втором этапе оставим источникЕ2,
а исключим источникЕ1 и
все источники внутри двухполюсника
(двухполюсник при этом станет пассивным).
Так как источникЕ2в схеме
(рис. 1.16,г) является единственным и
включен он в ветвь, где надо определить
ток, величина этого тока может быть
легко определена:
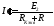
где Rэкв– эквивалентное сопротивление двухполюсника по отношению к зажимам рассматриваемой ветви при условии, что все источники внутри двухполюсника исключены.
Теперь
можно определить
 .
Так как
.
Так как ,
аЕ2=Uх,
окончательно получим:
,
аЕ2=Uх,
окончательно получим:

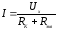 (1.51)
(1.51)
Таким образом, ток в любой ветви произвольной сколь угодно сложной схемы равен напряжению холостого хода этой ветви, деленному на сумму сопротивлений этой ветви и эквивалентного сопротивления остальной схемы по отношению к зажимам рассматриваемой ветви (при исключенных источниках).
Нетрудно составить схему, соответствующую
формуле (1.51) она приведена на рис. 1.17.
Отсюда видно, что любой активный
двухпоюсник по отношению ветви с
сопротивлением Rк может
быть заменен простой схемой замещения
из последовательно соединенных источника
с напряжениемUхи сопротивлениемRэкв.
Вопрос №7 Синусоидальные токи
Такие токи являются наиболее важным и наиболее часто применяемым частным случаем переменных периодических токов (рис. 4.1).
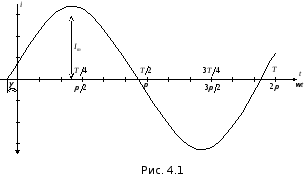
Закон изменения таких токов во времени в общем случае определяется выражением:
i=Imsin(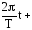 )
) (4.1)
(4.1)
Здесь Im– максимальное (амплитудное) значение тока;
 – начальная фаза тока.
– начальная фаза тока.
Периодом такого тока по времени является
Т, а по углу – 2.
Отношение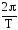 =называют угловой (круговой) частотой,
она показывает скорость изменения
фазового угла.
=называют угловой (круговой) частотой,
она показывает скорость изменения
фазового угла.
Так
как
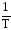 =f, то= 2f.
=f, то= 2f.
При частоте 50 Гц: = 314 (рад/с).
Тогда:
i = Im
sin (
t +
), (4.2)
), (4.2)
Если рассматриваются два синусоидальных тока, то их разность по фазе называют сдвигом по фазе и обозначают. Соответственно при= 0 токи называют совпадающими по фазе, при=1800=– противоположными по фазе.
Вопрос № 8 Действующее и среднее значение синусоидального тока
Так как синусоидальные токи всё время изменяются с течением времени, в практике удобно использовать те или иные их характеристики, усреднённые во времени.
Действующим(эффективным) значением синусоидального тока называют значение, численное равное постоянному току, при котором на некотором сопротивленииRвыделится та же мощность, что и при синусоидальном токе.
Для постоянного тока мощность
P=I2R(4.7)
На переменном токе мощность непрерывно изменяется, её мгновенное значение p=i2 R. Среднее значение мощности за период Т:
РСР=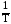

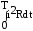 .
.
Для синусоидального тока i=Imsint:
Рср
=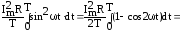



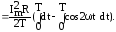 (4.8)
(4.8)
Здесь второй интервал равен нулю, как интеграл от синусоидальной функции в пределах целого периода, тогда
Рср=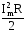 (4.9)
(4.9)
Приравняв (4.7) и (4.9), получим:
 (4.10)
(4.10)
Аналогично,
для напряжения
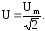
Эти значения синусоидального тока и напряжения используются в практике наиболее часто. Если не оговорено особо, то предполагается, что имеется в виду именно действующее значение (например, в номинальных паспортных данных аппаратуры и оборудования). Электроизмерительные приборы электромагнитной, электродинамической, ферродинамической, тепловой систем измеряют именно действующее значение.
Среднеезначение переменного тока – такое
значение неизменяющегося тока, при
котором за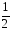 Т
по цепи протекает то же количество
электричества, что и при переменном
токе. Таким образом среднее значение
тока за
Т
по цепи протекает то же количество
электричества, что и при переменном
токе. Таким образом среднее значение
тока за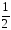 Т
на диаграмме рис. 4.4 образует прямоугольник,
равновеликий по площади полуволне
синусоиды переменного тока:
Т
на диаграмме рис. 4.4 образует прямоугольник,
равновеликий по площади полуволне
синусоиды переменного тока:

откуда:
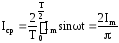 .
(4.11)
.
(4.11)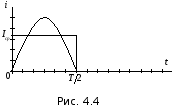
Аналогично для напряжения:
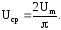 (4.12)
(4.12)
Отношение действующего и среднего значения токов называют коэффициентом формы кривой: КФ. Для синусоидального тока:

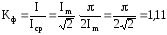 .
. (4.13)
(4.13)
В практике по отклонению величины kфот приведённого значения судят об отклонении реальной кривой тока от синусоидальной.
Вопрос №9 Изображение синусоидальных токов и напряжений с помощьювекторов
В практике расчётов электрических схем синусоидального тока непосредственное использование мгновенных значений токов приводит к весьма сложным аналитическим расчётам. Например, даже при использовании 1-го закона Кирхгофа приходится вычислять выражения вида:
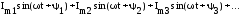
Поэтому в электротехнике принято представлять синусоидальные токи и напряжения в виде векторов.
Синусоидальный ток имеет 2 информационных признака (амплитуду и фазу), вектор – модуль и направление.
(Здесь и далее частоту будем полагать неизменной).
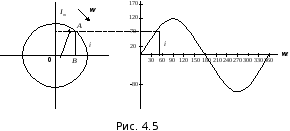
Из рис. 4.5 видно, что если ОА равно Im, то:

При изменении tвектор вращается, его проекция на вертикальную ось даёт мгновенное значение тока.
Рассмотрим теперь сложение двух синусоидальных токов одинаковой частоты (рис.4.6):
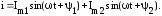
Из рис.4.6 видно, что для выполнения этой операции достаточно просуммировать векторы Im1иIm2, а затем найти проекцию суммарного вектора на вертикальную ось.
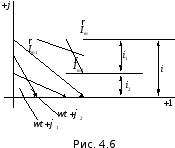
Аналогично может быть выполнено сложение и вычитание любого числа векторов.
Векторное сложение (вычитание) может быть выполнено только для токов одинаковой частоты, иначе векторы на диаграмме будут вращаться с разной скоростью, соответственно углы между ними будут непрерывно меняться.
Рисунок, на котором токи и напряжения какой-либо схемы изображены в виде векторов, называется векторной диаграммой.
Если модуль каждого вектора разделить
на
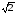 ,
получаем векторную диаграмму в действующих
значениях.
,
получаем векторную диаграмму в действующих
значениях.
Так как векторы вращаются и в течение времени Т каждый вектор поворачивается на угол 2, то в тех случаях, когда нам безразличен выбор момента времениt, для которого мы строим векторную диаграмму, один из векторов диаграммы может быть направлен произвольно. По существу, это равносильно произвольному выбору момента времени, для которого строится диаграмма. Это обстоятельство широко используется в практике, так как позволяет один из векторов направлять наиболее удобным образом (например, горизонтально или вертикально). Однако, направление всех остальных векторов выбирать произвольно уже нельзя.
Вопросы 10,11,12 Основные элементы электрической цепи на переменном синусоидальном токе
Рассмотрим простейшую электрическую цепь (рис.4.2) с последовательным соединением активного сопротивления R, индуктивностиLи ёмкости С в случае, если по ней протекает переменный синусоидальный токi=Imsint.

Напряжение на активном сопротивлении uа =iR. Следовательно , если токiизмеряется по синусоидальному закону, то напряжениеuа тоже изменяется по такому же закону. При этом
Uam =Im ·R. (4.3)
Напряжение на индуктивности
uL
=L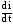 =ImLcost
=ImLcost
или uL = ImL sin(t + 900).
Таким образом, напряжение на индуктивности при синусоидальном токе также будет изменяться по синусоиде, но опережающейпо фазе синусоиду тока на 900эл.
Амплитудное значение при этом:
ULm=ImL(4.4)
По аналогии с (4.3) обозначим L= ХL и назовём эту величинуиндуктивным сопротивлением.Отметим, что в отличие отRиндуктивное сопротивление не является реальной физической величиной, хотя её и удобно использовать в практических расчётах. В частности, ХL будет иметь разные значения при различных частотах.
Напряжение на ёмкости:
uC
=
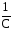
 it
= –
it
= –
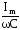 соs
t
= – Im
соs
t
= – Im
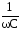 sin (t
– 900).
sin (t
– 900).
Следовательно при синусоидальном токе напряжение на ёмкости также будет изменяться по синусоиде, но отстающей по фазе от тока на 900эл.
Амплитудное значение напряжения на ёмкости:
UСМ=Im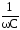 . ( 4.5)
. ( 4.5)
Обозначим
 = ХСи назовём эту величину
ёмкостным сопротивлением. Это сопротивление
также зависит от частоты.
= ХСи назовём эту величину
ёмкостным сопротивлением. Это сопротивление
также зависит от частоты.
Таким образом, при протекании по рассматриваемой цепи (рис.4.2) синусоидального тока напряжения на всех элементах схемы также будут синусоидальными. Отметим, что и приложенное ко всей схеме напряжение uбудет синусоидальным ( как сумма синусоид).
Очевидно, будет верным и обратное утверждение: при синусоидальных напряжениях будут синусоидальными все токи. Ни одна другая периодическая функция, кроме синусоидальной, не обладает такими свойствами.
Вновь рассмотрим схему рис.4.2. В
соответствии со 2-законом Кирхгофа для
этой схемы при токе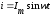 :
:
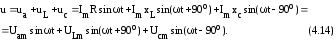
Построим для данной схемы векторную диаграмму, при этом первым вектором построен вектор Im, так как ток для этой схемы является общей величиной для всех элементов схемы. В соответствии с указаниями раздела 4.4 направим его, например, горизонтально (рис.4.7).
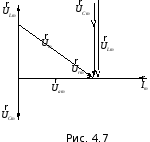
Тогда вектор
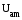 совпадает
по фазе с
совпадает
по фазе с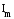 ,
вектор
,
вектор опережает
по фазе
опережает
по фазе на 90о, вектор
на 90о, вектор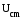 –
отстаёт на 90оот
–
отстаёт на 90оот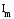 .
Просуммировав эти три вектора, получим
в соответствии с (4.14) вектор
.
Просуммировав эти три вектора, получим
в соответствии с (4.14) вектор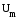 .
Разделив все вектора на
.
Разделив все вектора на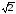 ,
получим векторную диаграмму в действующих
значениях.
,
получим векторную диаграмму в действующих
значениях.
Модуль этого вектора нетрудно найти из геометрических соображений:
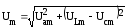
или, в действующих значениях:
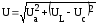 .
(4.15)
.
(4.15)
Индуктивные и ёмкостные элементы схемы обычно называют реактивными. Соответственно назовём UL–Uc=Ur– реактивным напряжением, тогда:
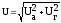 .
.
Направление
вектора
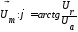 ,
следовательно:
,
следовательно:
Ua=Ucos.Ur=Usin.
Из диаграммы 4.7 видно, что напряжения U,Ua,Urобразуют прямоугольный треугольник, который называетсятреугольником напряжений.
Обозначим
 - полное сопротивление цепи.
- полное сопротивление цепи.
Тогда, разделив обе части выражения (4.15) на ток, получим:
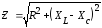
или
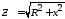 .
.
где х = хL– хс– реактивное сопротивление.
Видим, что сопротивления Z,R,xобразуют
прямоугольный треугольник (рис.4.8),
причёмтреугольник сопротивленийподобен треугольнику напряжений.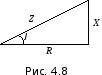
Рассмотрим теперь схему с параллельным соединением R,L,C(рис.4.9), в этой схеме общей величиной является напряжение, приложенное к элементам схемы, соответственно, с этого вектора и начнём построение векторной диаграммы.
Направив этот вектор произвольно
(например, вертикально) получим векторную
диаграмму рис.4.10 а (она построена сразу
в действующих значениях). В соответствии
с 1-м законом Кирхгофа из векторной
диаграммы получим: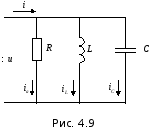
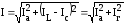 ,
(4.16)
,
(4.16)
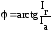 ,
(4.17)
,
(4.17)
то есть Ia,Ir,Iобразуют треугольник токов.
Обозначим
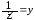 - полная проводимость схемы, тогдаI=Uy.
- полная проводимость схемы, тогдаI=Uy.
Разделив обе части (4.16) на U, получим:
 .
.
где
 - активная проводимость;
- активная проводимость;
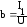 - индуктивная проводимость;
- индуктивная проводимость;
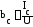 - ёмкостная проводимость;
- ёмкостная проводимость;
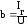 - реактивная проводимость.
- реактивная проводимость.
На рис.4.10б приведён треугольник
проводимостей, нетрудно увидеть,
что он подобен треугольнику токов,
поэтому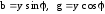 .
.
Отметим
также, что в общем случае при наличии в
каждой параллельной ветви нескольких
последовательно соединённых сопротивлений,
зависимости, связывающие проводимости
и сопротивления, имеют вид: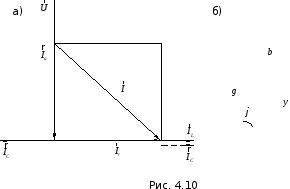
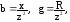 (4.18)
(4.18)
которые получим, подставив значения sinφиcosφиз треугольника сопротивлений. В частном случае, если в ветви имеется лишь одно сопротивление:
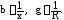
Рассмотренные выше схемы с последовательным либо с параллельным соединением сопротивлений практически исчерпывают виды схем, которые могут быть рассчитаны путём построения для них векторных диаграмм и использованием простых геометрических соотношений, полученных из них. Для более сложных схем со смешанным последовательно-параллельным соединением сопротивлений расчёт по приведённой выше методике становится чрезмерно громоздким и трудоёмким.
