Analiticheskaya_geom / 1_5_Pryamaya_v_prostranstve_Zadachi_o_pryamykh_i_pl

1.5. Лекция 5. Прямая в пространстве. Задачи о прямых

и плоскостях

Уравнения прямой, проходящей через данную точку и параллельной данному вектору. Уравнение прямой, проходящей через две заданные точки. Расстояние от точки до прямой. Расстояние между непараллельными прямыми. Проекция точки на плоскость. Проекция точки на прямую. Проекция прямой на плоскость параллельно заданному вектору. Общий перпендикуляр к двум скрещивающимся прямым.

Уравнение прямой, проходящей через данную точку

и параллельной данному вектору

Существует, причем единственная, прямая , содержащая заданную точку и параллельная ненулевому вектору . Такой вектор называется направляющим вектором прямой . Для произвольной точки пространства имеем (рис. 10) логическую цепочку

Уравнение

(5.1)

называется векторным уравнением прямой. Вектор называют вектором сдвига прямой.

Условие параллельности векторов и можно записать в виде

,

или

. (5.2)

Уравнение (5.2) называется векторно-параметрическим уравнением прямой. Расписывая его в декартовой системе координат, получим параметрические уравнения прямой

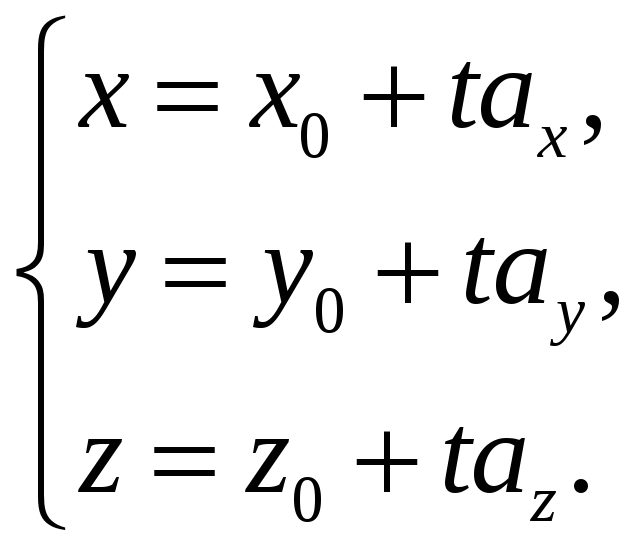(5.3)

Если параметр пробегает , точка с координатами из (5.3) пробегает прямую.

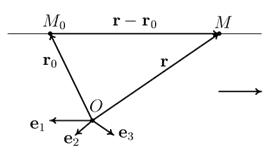
Рис. 10. Уравнение прямой

Условие (5.1) коллинеарности векторов в координатах примет вид пропорции

(5.4)

где .

Если обращается в нуль одна из координат направляющего вектора, например , то уравнения прямой принимают вид

Эта прямая лежит в плоскости .

Уравнение прямой, проходящей через две заданные

точки и

В качестве направляющего вектора прямой можно взять вектор , а в качестве данной точки прямой – точку . Тогда уравнение (5.1) примет вид

или в координатах

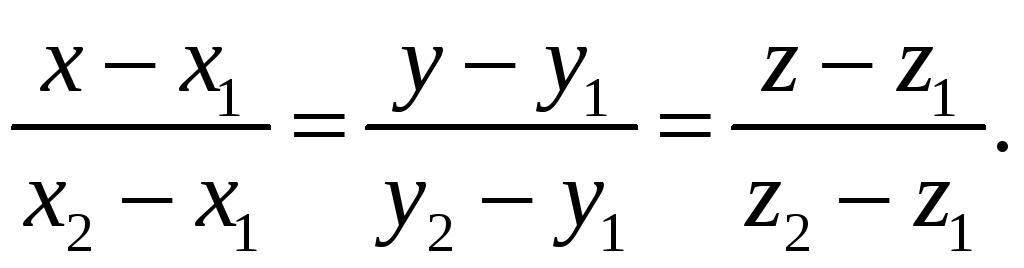
Расстояние от точки до прямой

Пусть прямая задана уравнением , а точка – радиус-вектором . Расстояние от точки до прямой равно можно найти, разделив площадь параллелограмма, построенного на векторах и , на длину его основания (рис. 11).

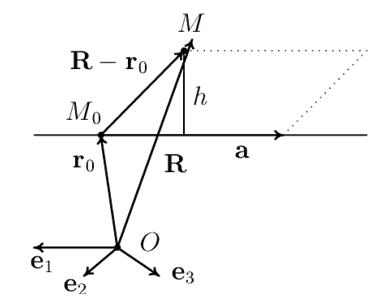
Рис. 11. Расстояние от точки до прямой

В результате получим формулу расстояния от точки до прямой

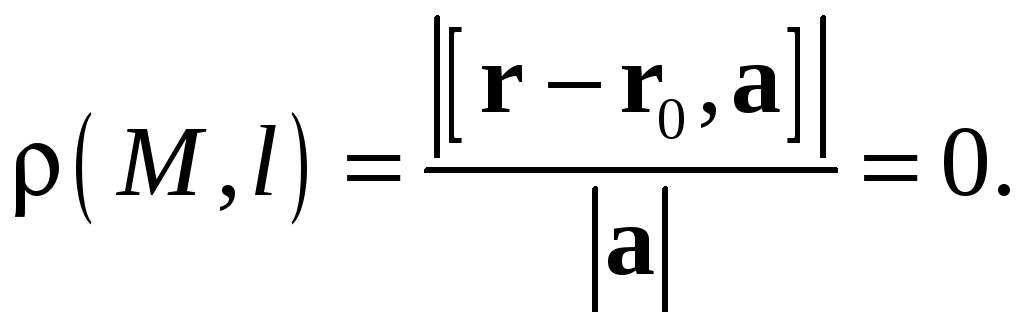(5.5)

Упражнение. Записать расстояние от точки до прямой в прямоугольных декартовых координатах.

Расстояние между непараллельными прямыми

Рассмотрим две непараллельные прямые

Существуют параллельные плоскости и такие, что

.

В качестве направляющих векторов обеих плоскостей можно взять пару векторов , , а в качестве начальных точек - точки с радиус-векторами и , соответственно, для плоскостей , . Искомое расстояние между прямыми можно найти, разделив объем параллелепипеда, построенного на векторах , , на площадь его основания (рис. 12). Получим

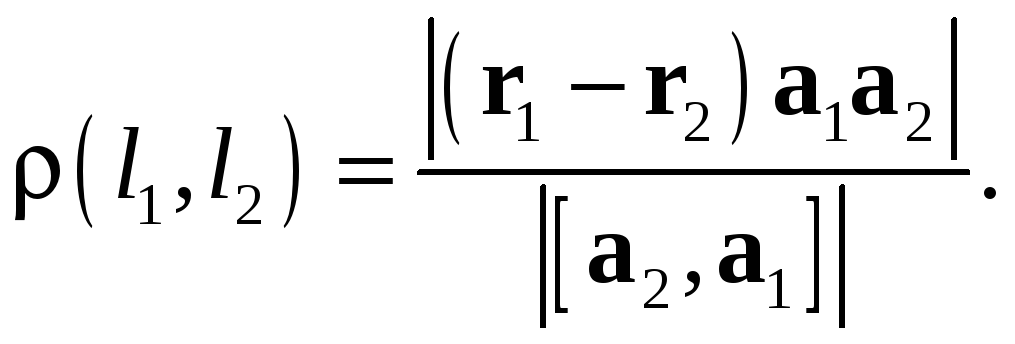
Рис. 12. Расстояние между непараллельными прямыми

Из приведенных рассуждений получаем также

Предложение. Прямые и пересекаются тогда и только тогда, когда

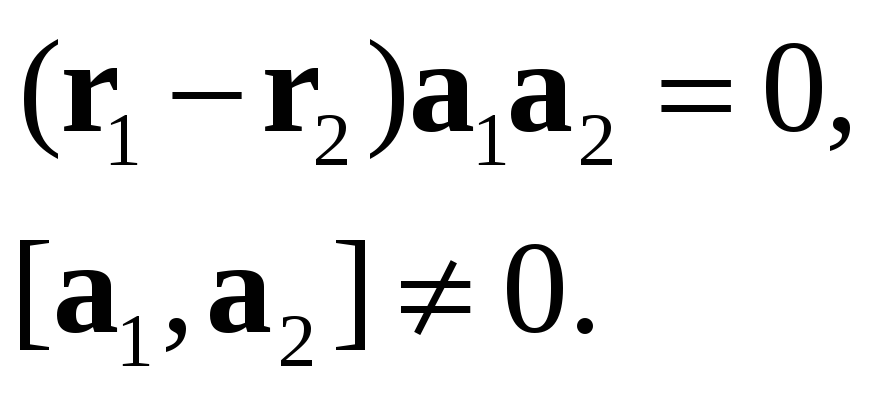
Проекция точки на плоскость

Найдем радиус-вектор проекции точки на плоскость , заданную уравнением

Прямая проходит через и перпендикулярна плоскости. Подставляя значение для из уравнения прямой в уравнение плоскости, получим . Отсюда 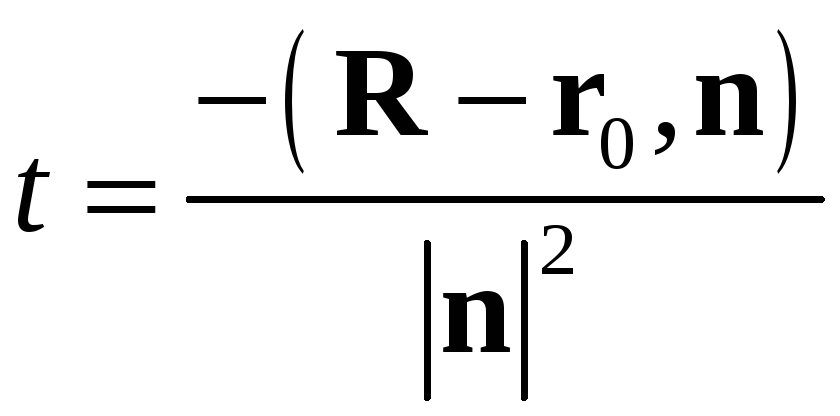. Подставив найденное значение в уравнение прямой, получим радиус-вектор искомой проекции

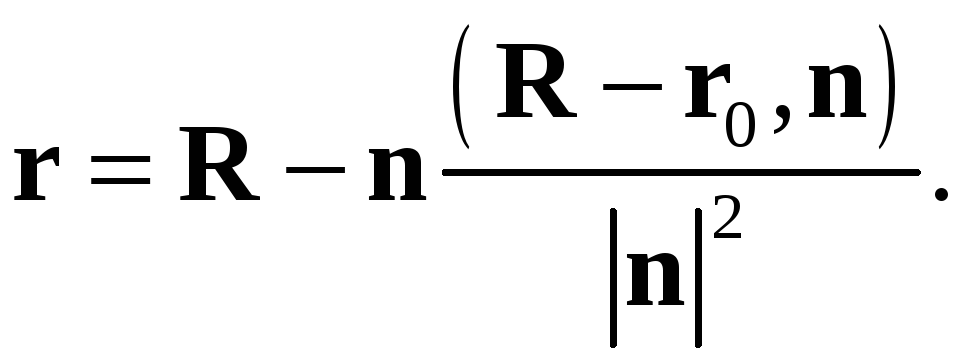
Проекция точки на прямую

Пусть прямая задана уравнением и дана точка с радиус-вектором . Построим плоскость , перпендикулярную прямой и проходящую через точку . В качестве нормального к плоскости вектора можно взять вектор , а в качестве начальной точки плоскости – точку . Тогда есть уравнение искомой плоскости. Точка пересечения этой плоскости с прямой и есть проекция точки на прямую . Найдем эту точку, решая относительно и систему уравнений

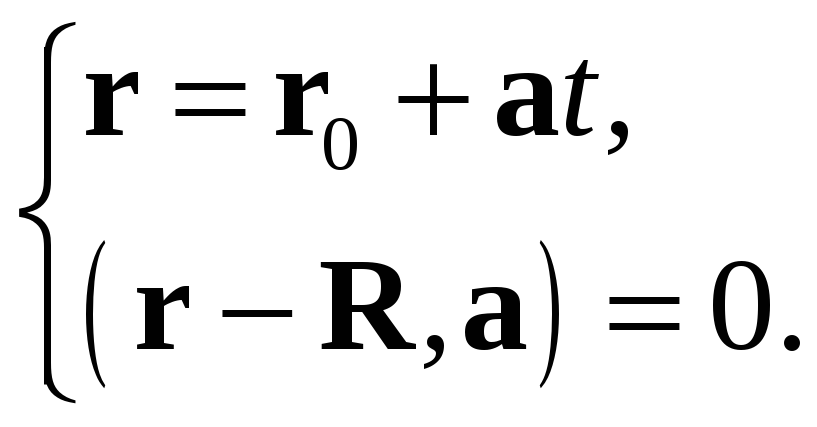
Подставляя из первого уравнения во второе, получим

Отсюда

и

.

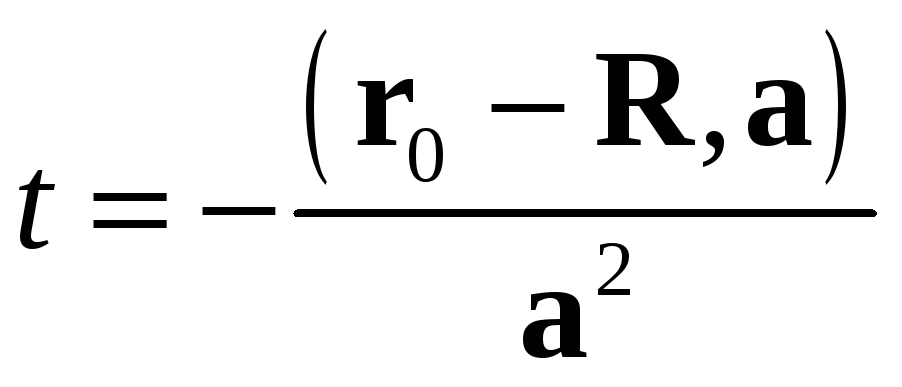Подставляя найденное значение в первое уравнение системы, получим радиус-вектор искомой точки

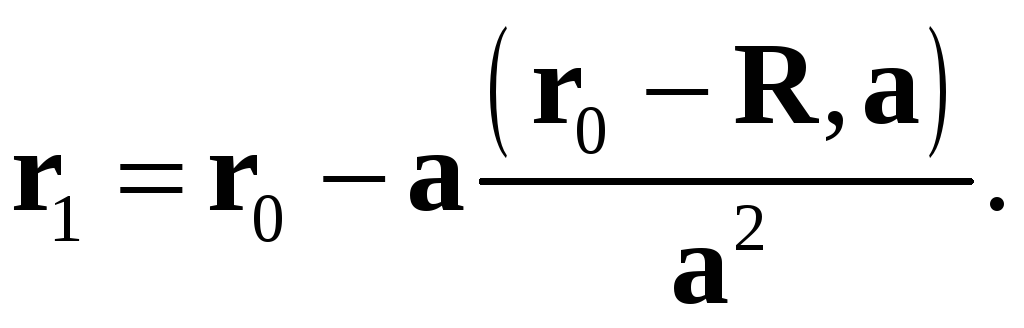
Проекция прямой на плоскость параллельно заданному вектору

Пусть плоскость задана уравнением , прямая – уравнением . Требуется составить уравнение проекции прямой на плоскость параллельно вектору . Будем считать, что векторы не коллинеарны, ибо в противном случае проекцией прямой на плоскость является точка. Направляющий вектор проекции можно искать в виде комбинации , перпендикулярной вектору (рис. 13).

Рис. 13. Проекция прямой на плоскость

Так как длина вектора с нам безразлична, то мы можем положить .

Из условия

получим и

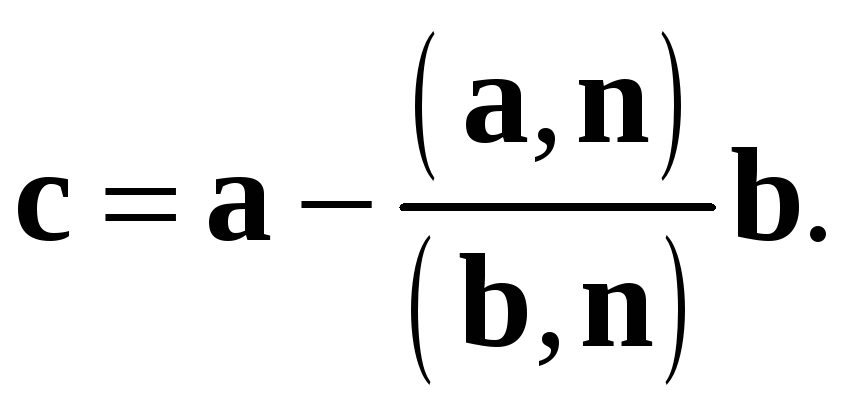
Найдем радиус-вектор точки пересечения плоскости и прямой .

Подставляя значение из уравнения прямой в уравнение плоскости, получим . Отсюда . При этом значении уравнение прямой даст искомый радиус-вектор

Имея радиус-вектор начальной точки проекции и ее направляющий вектор , запишем, наконец, уравнение проекции

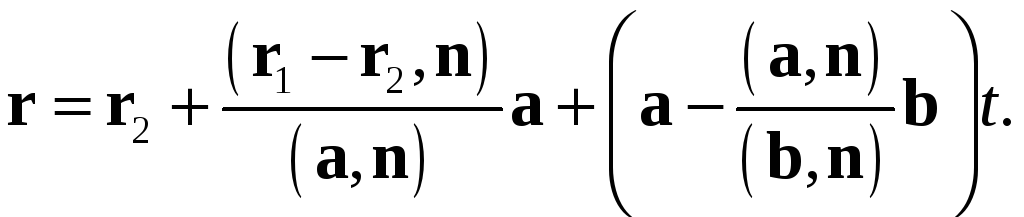
Другой вариант решения этой задачи заключается в построении проекции как пересечения двух плоскостей: плоскости и плоскости , порожденной векторами и проходящей через точку пересечения прямой с плоскостью .

Общий перпендикуляр к двум скрещивающимся прямым

Пусть прямые и не параллельны, т.е.. Вектор перпендикулярен обеим прямым. Поэтому плоскость

(5.6)

проходит через первую прямую и общий перпендикуляр, а плоскость

(5.7)

– через вторую прямую и общий перпендикуляр к обеим прямым. Следовательно, общий перпендикуляр можно задать системой уравнений (5.6) и (5.7) как пересечение плоскостей. Чтобы найти его начальную точку, можно решить совместно уравнение первой прямой и уравнение плоскости (5.7). Направляющим вектором является вектор .

Рассмотрим другой способ решения этой задачи. На первой прямой возьмем произвольную точку с радиус-вектором , а на второй – точку с радиус-вектором . Подберем значения параметров так, чтобы вектор

был перпендикулярен обоим векторам и . Для этого мы должны решить относительно систему

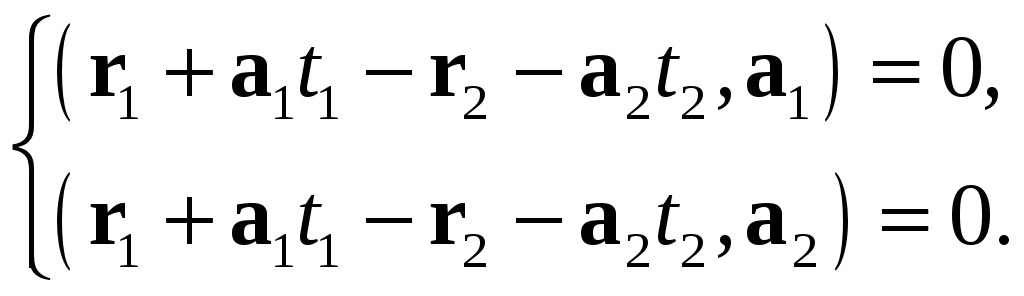
Преобразуем ее к виду

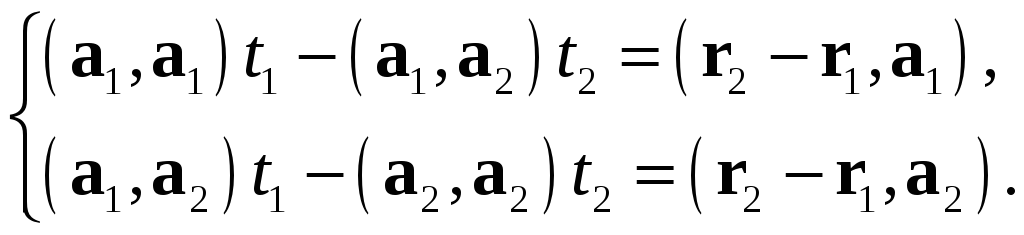
Главный определитель этой системы

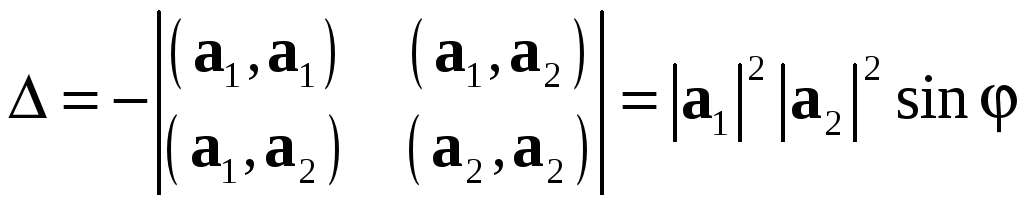
отличен от нуля. По правилу Крамера эта система имеет единственное решение

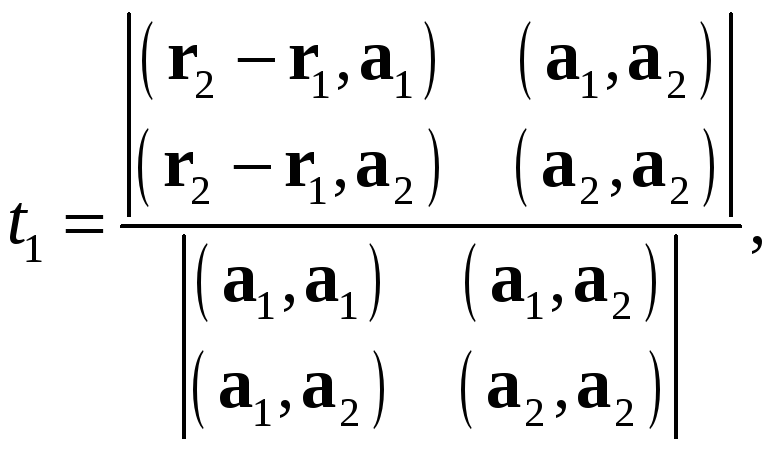
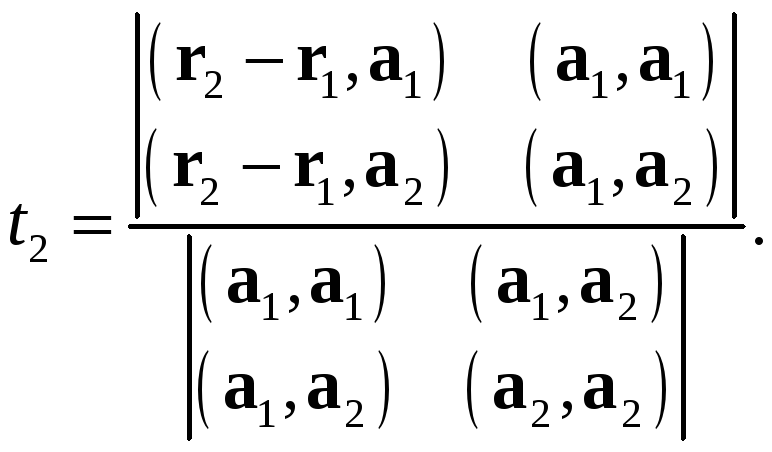
Тем самым определятся точки и . Осталось записать уравнение прямой через эти точки.

Изложенный метод годится для построения общего перпендикуляра к двум скрещивающимся прямым в пространстве размерности и выше трех.

Упражнения

5.1. Точка определяется радиус-вектором . Составить уравнение прямой, проходящей через точку перпендикулярно плоскости .

5.2. Точка определяется радиус-вектором . Составить уравнение плоскости, проходящей через точку перпендикулярно прямой .

5.3. Составить векторное уравнение плоскости, проходящей через прямую и точку , не лежащую на этой прямой.

5.4. Даны точка и плоскость . Найти радиус-вектор точки , симметричной с относительно плоскости.

5.5. Даны точка и прямая . Найти радиус-вектор точки , симметричной с относительно прямой.

5.6. Составить уравнение прямой, пересекающей прямую под прямым углом и проходящей через точку , не лежащую на данной прямой (перпендикуляра, опущенного из точки на прямую .

5.7. Составить уравнение прямой, пересекающей две скрещивающиеся прямые и и проходящей через точку , не лежащую ни на одной из этих прямых.

5.8. Найти расстояние между двумя параллельными плоскостями и .

5.9. Составить уравнение прямой, которая параллельна прямой и пересекает прямые , .

Вопросы для самопроверки

1. Дайте геометрическую иллюстрацию векторно-параметрическому уравнению прямой.

2. Как перейти от векторно-параметрического уравнения прямой к каноническим и параметрическим уравнениям?

3. Как найти направляющий вектор прямой, проходящей через две заданные точки?

4. Как найти направляющий вектор прямой, являющийся пересечением двух плоскостей?

33