1.2. Лекция 2. Скалярное, векторное и смешанное

произведения

Скалярное произведение. Векторное произведение. Смешанное произведение. Двойное векторное произведение. Решение векторных уравнений. Законы физики и векторный язык.

Скалярное произведение

Определение. Пусть a, b – ненулевые вектора, приведенные к общему началу. В качестве угла между ними можно принять как угол , так и угол, косинусы которых одинаковы. Значит формула

, (2.1)

где и– длины векторовиb, однозначно определяет некоторое число , называемое скалярным произведением двух векторовиb. Если или , то, по определению, .

Скалярное произведение возникло в физике. Работа, которую совершает сила при перемещении тела из точки в точкуB (рис.2), равна

(2.2)

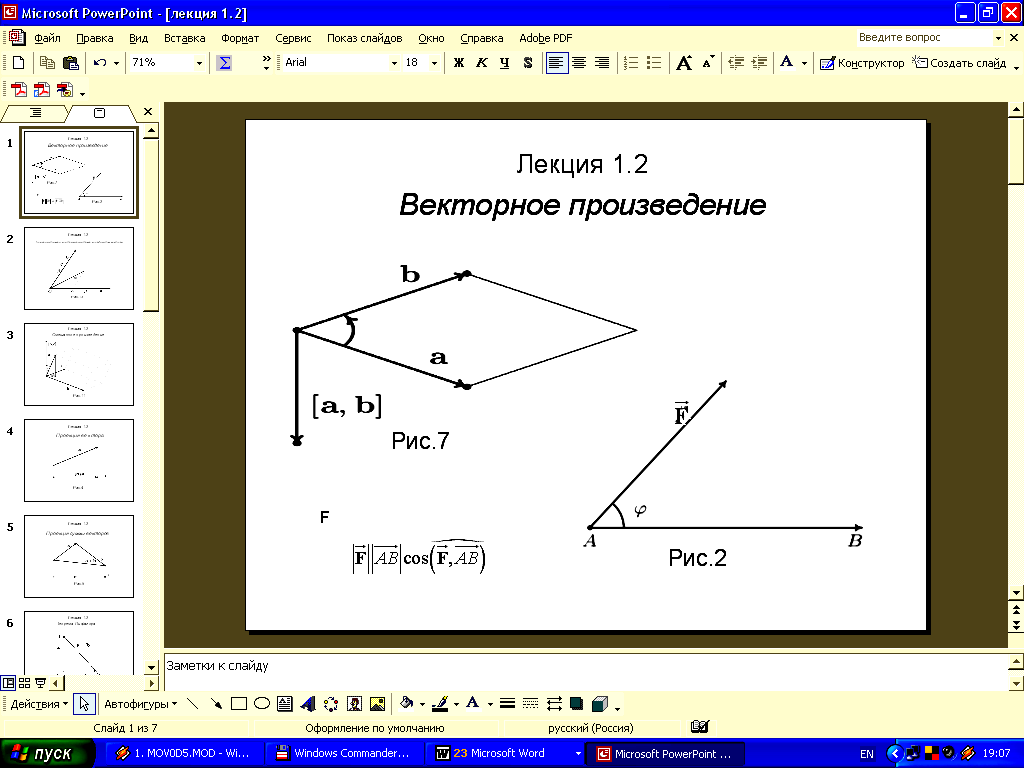
Рис. 2. Работа силы

В этом выражении мы узнаем скалярное произведение

Геометрические свойства скалярного произведения

Непосредственно из определения скалярного произведения легко получить следующие свойства:

1) , (2.3)

2) , (2.4)

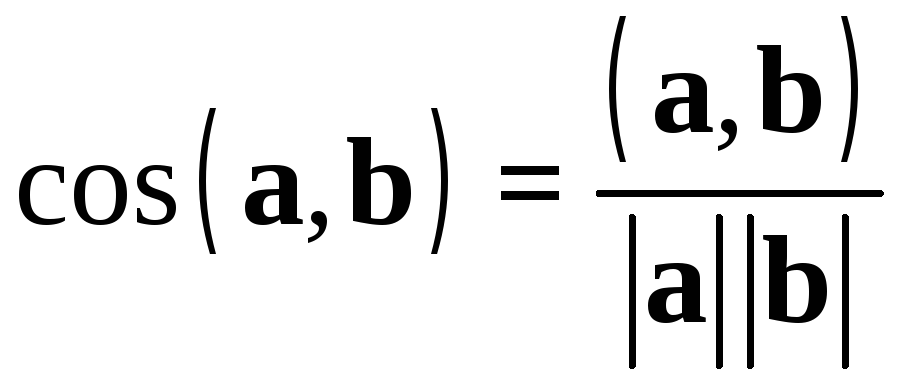3) . (2.5)

Таким образом, с одной стороны, скалярное произведение определено через длины векторов и угол между ними, с другой − длины векторов и угол между ними выражаются через скалярное произведение. Эта взаимная определимость является исходной идеей для введения понятия расстояния и угла в абстрактных линейных пространствах.

Векторы иназываютсяортогональными, если их скалярное произведение равно нулю:

. (2.6)

При иэто равносильно тому, что угол между векторамииравен.

Проекцией вектора на прямуюназывается вектор, началом которого служит проекция начала вектора, а концом - проекция конца векторана прямую(рис.3). Проекцию векторана неориентированную прямую, определяемую вектором, будем обозначать.

Лемма 2.1. .

Доказательство легко усмотреть из рис. 4.

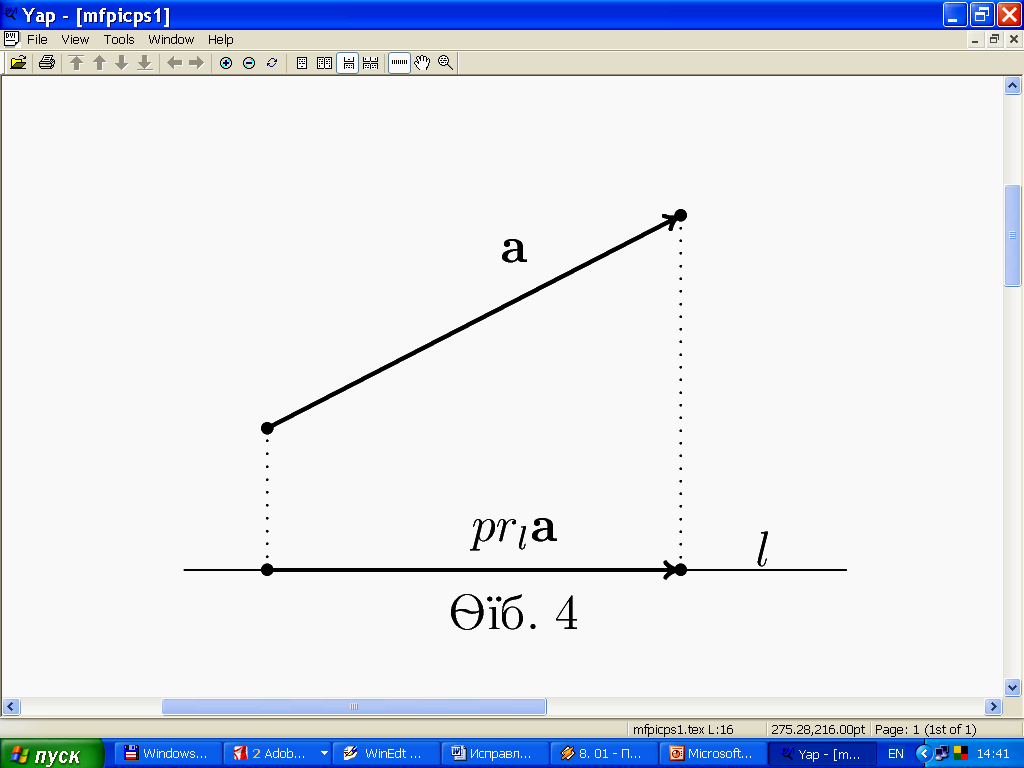
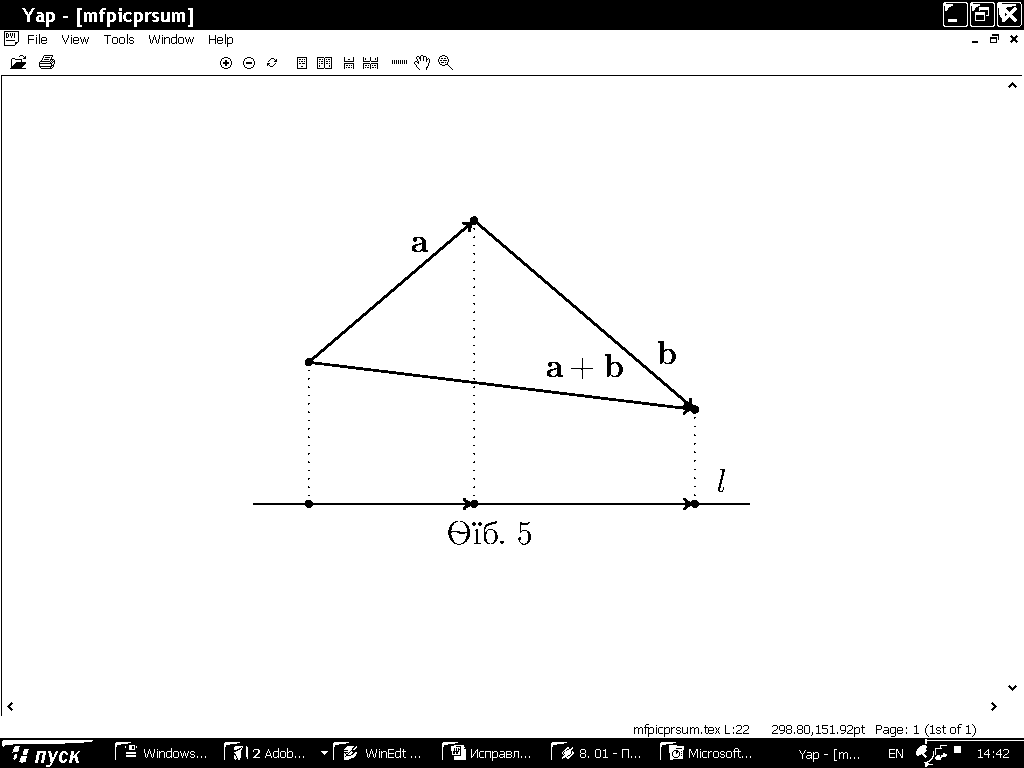
Рис. 3. Проекция вектора Рис. 4. Проекция суммы векторов

на прямую на прямую

Лемма 2.2. .

Доказательство. Действительно, .

Лемма 2.3..

Доказательство. Упражняйтесь. 

Алгебраические свойства скалярного произведения

Так называют следующие свойства:

1) (a,b)=(b,a) – коммутативность;

2) − однородность;

3) (a+b,c)=(a,c)+(b,c) − дистрибутивность;

4) − положительная определенность.

Свойства 1, 2, 4 легко вывести из определения. Докажем свойство 3. По лемме 2.2

. (2.7)

Отсюда и из леммы 2.1

. (2.8)

С другой стороны, по лемме 2.2

. (2.9)

Пусть – орт векторат.е. вектор, имеющий единичную длину и сонаправленный векторус (Легко проверить, что 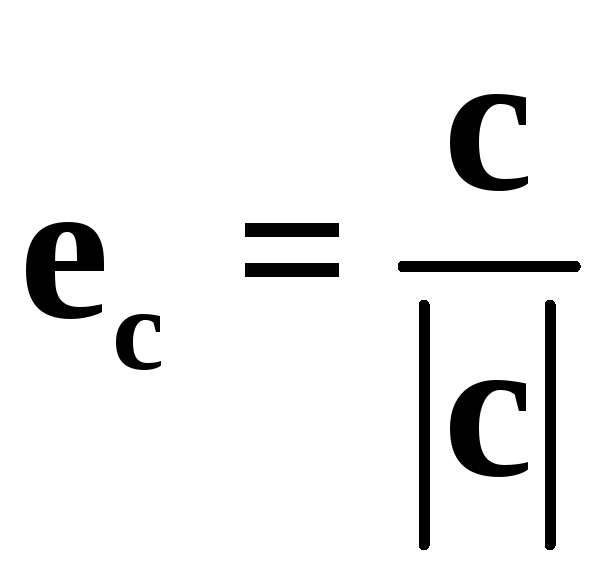.) Тогда для некоторых чиселимеем

, , . (2.10)

Подставляя это в (2.8), (2.9), получим

, (2.11)

, (2.12)

что и требовалось доказать.

Если векторы и ортогональны, то

. (2.13)

В качестве приложения скалярного произведения докажем известную из школьного курса теорему косинусов. В треугольнике обозначим,и. Тогдаи

, (2.14)

что и требовалось.

При треугольникпрямоугольный и теорема косинусов дает теорему Пифагора.