Беляев Ю.Н. Введение в векторный анализ

Ÿ 4.

Разложение вектора на составляющие

41

~

есть линейная комбинация двух неколлинеарных век-

вектор f

~

~

~

торов ~g и h: f = f1~g + f2h:

~

~g

h

f1~g

~

~

~g

f

f

~

~

f2h

Ðèñ. 26

h

a)

b)

Для нахождения координат

f1 è

~

f2 вектора f в базисе ~g

~

(ñì. ðèñ. 26a)

нужно

параллельным

переносом

векто-

è h

~

~

ров f , ~g, h совместить их начала и построить параллелограмм,

~

~

стороны которого параллельны векторам ~g и h, а вектор f яв-

ляется диагональю этого параллелограмма (см. рис. 26b). Такое

разложение единственно. Доказательство последнего утвержде-

ния проводится подобно тому, как это было сделано ранее для

пространственного случая.

П р и м е р 17. Найдем коорди-

наты векторов

~

~

F5

è F10 из задачи 6

~

в базисе

~

~

из той же задачи (см.

F1; F6

F10

ðèñ. 11).

~

~

По построению (рис. 27)

F1

F6

~

1 ~

~

~

~

~

:

1

~

F5

= 2 F1

+ F6

; F10

= F1

F6

2 F~1

Следовательно,

координатами век-

F6

~

~

~

~

в базисе

являются

F5

òîðà F5

F1; F6

числа

1

~

Ðèñ. 27

2 и 1; а вектора

F10 ñî-

ответственно 1 и 1.

Расмотрим теперь случай, когда базис состоит лишь из одного вектора. Такая ситуация реализуется для множества векторов, параллельных некоторой прямой; базисом может быть любой ненулевой вектор из этого множества.

Подытоживая сказанное о векторных базисах, еще раз отметим, что: 1) любые три некомпланарных вектора образуют базис в тр¼хмерном пространстве; 2) любые два неколлинеарных вектора образуют базис на плоскости, в которой они лежат; 3) один (ненулевой) вектор является базисом для множества векторов ему параллельных. Согласно определению, минимальное

42	Глава 1. ОСНОВНЫЕ СВЕДЕНИЯ ИЗ АЛГЕБРЫ

число линейно независимых векторов, с помощью которых любой другой вектор данного множества может быть однозначно представлен в виде линейной комбинации, называется размерностью данного векторного множества. Соответственно, множество векторов в первом случае есть трехмерное векторное пространство, во втором двумерное, а множество векторов, параллельных одной прямой одномерное векторное пространство.

Задачи

20. Известны разложения двух векторов p~ и q~ по трем

~ ~ ~

некомпланарным векторам b1; b2; b3:

~	~	~	~	~	~	:
p~ = p1b1	+ p2b2	+ p3b3	; q~ = q1b1	+ q2b2	+ q3b3

Какая зависимость должна существовать между коэффициентами этих разложений, если 1) p~ = ~q; 2) p~ и ~q коллинеарны?

21.	×òî	можно сказать		о взаимном расположении век-
торов	~	~	åñëè îíè	связаны линейной зависимостью
	~a; b;	~c; d,
~		~	~

~a + b + ~c + d = 0? Рассмотреть следующие варианты:

1)=6 0; =6 0; =6 0; =6 0;

2)= 0; =6 0; =6 0; =6 0;

3)= 0; = 0; =6 0; =6 0;

4)= 0; = 0; = 0; =6 0:

22. Разложить вектор			~	~		~c по тр¼м некомпланарным
			D = b 1
~	~	~		~		~	~
векторам: A = ~a b + ~c; B = b +					2~c; C = ~a + b:
			~		~
23. Разложить вектор A = ~a+b+~c по трем некомпланарным
~	~		~		~	~	~
векторам: B = ~a + b 2~c; C = ~a b и D = 2b + 3~c:
							~
24. Дано разложение вектора ~c = ~a + b по двум неколли-

~
неарным векторам ~a и b. В каком случае коэффициенты разло-
жения и (или) равны нулю?
~	~ ~
25. Найти координаты вектора Fi	в базисе Fj ; Fk . Âñå òðè

вектора берутся из задачи 6 (см. рис. 11). Значения номеров i,

~ ~ ~

j, k векторов Fi, Fj ; è Fk выбираются из Таблицы согласно двузначному номеру варианта mn, первая цифра которого m

~

определяет номер вектора Fi, а вторая цифра n номера j и

Ÿ 5. Проекции вектора																	43
k векторов		~			~
		Fj		è Fk . Например, в варианте 00 требуется найти
						~					~	~
координаты вектора F5								в базисе F1; F6.
						Т а б л и ц а к задаче 25
	m		0		1		2		3	4	5		6		7	8	9
	i		5		6		7		8	9	1		2		3	10	4
	n		0		1		2		3	4	5		6		7	8	9
	j		1		2		3		4	5	4		10		6	7	9
	k		6		5		4		2	1	7		8		9	3	10

Ÿ5. Проекции вектора

5.1.Проекция вектора на плоскость. Пусть даны вектор ~a и плоскость p (см. рис. 28). Опустим из начала A и конца B вектора ~a перпендикуляры AAp è BBp на плоскость

p. Основания перпендикуляров Ap è Bp являются проекциями
			!	(направленный от Ap
точек A и B на плоскость p. Вектор ApBp
ê Bp) называется проекцией вектора ~a на плоскость p.
			N	~a2
~a	B	~a1			K
			~s
A		M
	p		n		p
Ap	Bp	m			k
Ðèñ. 28			Ðèñ. 29

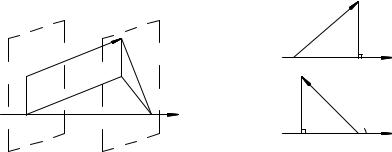
Возьмем два вектора ~a1 è ~a2 и плоскость p (рис. 29). Построим сумму ~s данных векторов и спроектирум их и их сумму

~s на плоскость p. Для этого из точек M , N , K опускаем перпен-

! !

дикуляры M m, N n, Kk на плоскость p. Векторы mn, nk суть

!

проекции данных векторов на плоскость p, а вектор mk есть

проекция их суммы ~s на ту же плоскость. Из рисунка 29 вид-

! ! !

но, что mk = mn + nk. Этот результат нетрудно обобщить на произвольное число N складываемых векторов, а именно: про-

екция суммы векторов на некоторую плоскость p равна сумме проекций складываемых векторов на эту же плоскость

X	p	X
N	~ai!	= N	~aip :	(1.51)
i=1		i=1

44	Глава 1. ОСНОВНЫЕ СВЕДЕНИЯ ИЗ АЛГЕБРЫ
5.2.	Проекция вектора на ось. Осью называется пря-

мая линия, которой приписано определенное направление (задаваемое, например, единичным вектором).

Проведем через начало A и конец B вектора ~a (рис. 30) плоскости pA è pB перпендикулярно оси `. Обозначим точки пересечения этих плоскостей с осью ` через A` è B`. Это будут основания перпендикуляров, опущенных из начала и конца вектора ~a на ось `.

Проекцией вектора ~a на ось `, задаваемую вектором единич- ной длины ~el, называется длина отрезка A`B`, взятая со знаком

(+), если направление этого отрезка совпадает с направлением оси `, и со знаком ( ) в противоположном случае. Это опре-

деление можно записать следующим образом:
	>		d
	<	A`B`; åñëè (~a; ~e`) < =2;
a` =	8		A`B`; åñëè (~a; ~e`) > =2;		(1.52)
	:	0;	d	d
	>		åñëè (~a; ~e`)
				= =2;

ãäå a` обозначает проекцию вектора ~a на ось `.

Заметим, что в отличие от проекции вектора на плоскость, являющейся вектором, проекция вектора на ось является вели- чиной скалярной.

	pA				a)	~a
			B			~a; ~e	)
A		~a	pB		0	)( d`	a`	~e`
		a	B0	~e`	b)	~a
								d`
A`			B`				_(~a; ~e`)
						a`	0	~e

Рис. 30 Рис. 31 Рассмотрим более подробно случай, когда угол между век-

тором и осью острый (рис. 30). Из точки A` проведем прямую, параллельную вектору ~a до пересечения с плоскостью pB â òî÷- êå B0. Четырехугольник ABB0A` по построению будет паралле-

0	6		0	A	B	~a; ~e	): Соединим
			B
лограммом. Поэтому A`B = a; è				`		` = ( d`

Ÿ 5. Проекции вектора

45

отрезком прямой точки B0 è B`: Отрезок B0B` лежит в плоскости pB ; поэтому он перпендикулярен оси `: Следовательно, треугольник A`B0B` прямоугольный, и в нем гипотенуза A`B0 равна длине a вектора ~a, а проекция A`B` = a` есть длина катета, прилежащего к углу 6 B0A`B`:

Проекцию свободного вектора на ось можно сделать более наглядной. Выберем на оси ` начало отсчета точку 0. Будем приписывать точкам оси, лежащим от т. 0 в направлении оси `, положительные значения, а точкам оси, лежащим по другую сторону от 0, отрицательные значения. Параллельным переносом совместим начало вектора ~a с т. 0 и опустим перпендикуляр из конца вектора ~a на ось `: Выбирая плоскость, проходящую через векторы ~a и ~e`; за плоскость чертежа, мы

d

получаем рис. 31a, когда угол (~a; ~e`) между вектором ~a и осью

`острый, и рис. 31b когда (~a; ~e`) > 90 :

5.3.Свойства проекции вектора на ось. Любую ось можно рассматривать в качестве координатной оси прямоугольной системы координат. В этом смысле проекция вектора на ось есть частный случай координаты вектора. Поэтому проекции векторов на оси, согласно формулам (1.47), (1.49), (1.50), обладают свойствами:

1) если два вектора равны, то равны и их проекции на любую ось

~	(1.53)
~a = b ) a` = b`;

2) проекция суммы векторов на любую ось равна алгебраиче- ской сумме проекций этих векторов на ту же ось, то есть

N	N
X	X
åñëè ~s = ~ai; òî s` =	ai`;	(1.54)
i=1	i=1

3) при умножении вектора ~a на любое число его проекция на произвольную ось ` умножается на число , а именно:

åñëè ~a = ~c; òî c` = a`:

(1.55)

46	Глава 1. ОСНОВНЫЕ СВЕДЕНИЯ ИЗ АЛГЕБРЫ

Ÿ6. Приложение к тригонометрии

6.1.Проекции единичного вектора. Понятие проекции вектора на ось тесно связано c синусом и косинусом угла. Напомним их определения.

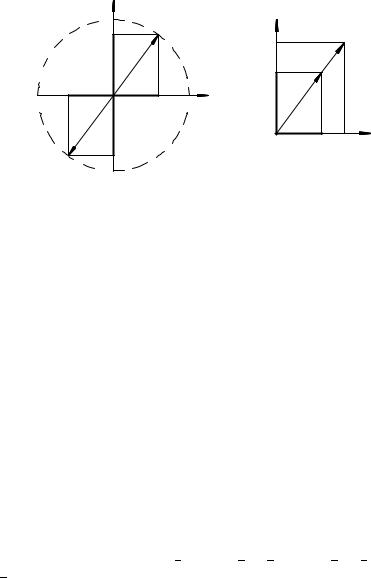
Возьмем на плоскости (рис. 32) две взаимно перпендикулярные оси x и y: Из точки их пересечения, взятой за нуль отсчета, проведем вектор единичной длины ~ea: Обозначим угол между ~ea и осью x буквой ' (положительный угол отсчитывается против хода часовой стрелки от оси x). Возможные положения конца вектора ~ea образуют круг единичного радиуса.

Проекция единичного вектора на ось y называется синусом угла ' и обозначается sin '; а проекция на ось x косинусом угла ': cos ':

Ясно, что при любом значении угла ' функции sin ' и cos ' не превосходят по модулю единицу: j sin 'j 1; j cos 'j 1:

При 0 ' < =2 и 3 =2 < ' 2 проекция вектора на ось x положительна (cos ' > 0). Если =2 < ' < 3 =2, то проекция вектора на ось x отрицательна.

6.2. Тригонометрическая форма записи проекции.

Используя определения синуса и косинуса, можно представить проекции вектора ~a произвольной длины a на оси x и y в виде

ax = a cos '; ay = a sin ':

Покажем это для случая 0 < ' < =2, когда тригонометри- ческие функции sin ' и cos ' можно рассматривать как отношения катета (противолежащего углу и прилежащего к углу соответственно) прямоугольного треугольника к гипотенузе (см. рис. 33). Действительно, из подобия треугольников OA0A0x èOAAx следует:

	OAx0	=	OAx	;		èëè	cos ' =		ax		;
	OA0		OA						a
A0Ax0		=	AAx		;	èëè	sin ' =	ay			:
	OA0		OA						a

Ÿ 5.	Проекции вектора							47
	Таким образом проекцию вектора на ось `, определяемую
формулой (1.52), можно записать в более компактной форме:
				~a; ~e	):			(1.56)
			y	a` = a cos( d`
		1				y
		sin '	~ea		ay		~a	A
			)'	x		~ea	A0
		cos('+ )			sin '
	-1	0	cos '	1
		-~ea	sin('+ )			)'	Ax0 Ax
					0	cos '	ax x
		-1				Ðèñ. 33
		Ðèñ. 32
	Сумма квадратов проекций вектора на взаимно перпенди-
кулярные оси, согласно теореме Пифагора, равна квадрату мо-
дуля вектора. Отcюда следует

6.3.Основное тригонометрическое тождество

sin2 ' + cos2 ' = 1:

(1.57)

6.4. Формулы приведения. Если изменить направление вектора на противоположное, то его проекция на ось изменит знак. Соответствующие построения для вектора единич- ной длины ~ea приведены на рис. 32. Очевидно,

sin(' + 180 ) = sin '; cos(' + 180 ) = cos ': (1.58)

Отметим здесь еще два соотношения между синусом и косинусом:

sin(' 90 ) = cos '; cos(' 90 ) = sin ':

(1.59)

6.5. Теорема синусов. Рассмотрим ABC (рис. 34). Обозначим углы при вершинах ABC теми же буквами, что и сами вершины, а именно: 6 CAB 6 A; 6 ABC 6 B; 6 BCA

6 C:

48	Глава 1. ОСНОВНЫЕ СВЕДЕНИЯ ИЗ АЛГЕБРЫ
				~
Спроектируем векторное равенство ~c = b+~a на направление
!	~	6			6
DB; перпендикулярное b: Получим c cos				ABD = a cos			DBC:

Перепишем это равенство, используя формулу (1.59), в виде

c sin A = a sin C:
Аналогично доказываются равенства: b sin A							= a sin B è
c sin B = b sin C:
Эти три равенства обычно записывают в виде единой фор-
ìóëû	sin A		sin B		sin C
		=		=		;	(1.60)
	a		b
					c

которая называется теоремой синусов.

A4

	B					~a4
~c		~a				)4'
	~			~s4		A3
	b				~s3
A	D	C	Ðèñ. 35			~a3
	Ðèñ. 34				~s2	)3'
						A2
					~a2
			.,
					)2'

A0 ~s1 = ~a1 A1

П р и м е р 18. Рассмотрим сумму ~sn компланарных век-

торов ~a1, ~a2; : : : ; ~an, таких, что каждый	èç	векторов ~aj+1
(j = 1; : : : ; n 1) повернут относительно ~aj	íà	îäèí è òîò æå

угол 2', и длины складываемых векторов одинаковы: a = a1 =

	a2 = : : : = an.
	1. Покажем, что	sin n'
	sn = a		:	(1.61)
		sin '

Будем обозначать окончания складываемых векторов ~aj (j = 1; : : : ; n) буквами Aj соответственно, а начало первого A0. Для наглядности на рис.35 показаны первые четыре складываемые векторы и суммы ~s1, ~s2, ~s3 è ~s4, когда ' < =4.

Нетрудно заметить, что получающиеся в результате построения многоугольники A0A1 : : : Aj , основаниями которых являются векторы ~sj , симметричны относительно прямой, проходя-

Ÿ 5. Проекции вектора

49

щей через середину соответствующего основания sj перпендикулярно последнему. Следовательно, угол между векторами ~a1 è ~sj равен углу между векторами ~aj è ~sj :

d	d		)
(~a1; ~sj ) = (~aj ; ~sj ):		(

d

По условию (~aj 1;~aj ) = 2'. Поэтому внутренние углы многоугольника A0A1 : : : Aj при вершинах A1; A2; : : : ; Aj 1 равны по (180 2') и для суммы внутренних углов этого многоугольника, используя формулу ( ), можно записать равенство

		1)(180		d		1)180 :
(j				2') + 2(~aj ; ~sj ) = (j

Отсюда находим

d

(~aj ; ~sj ) = (j 1)':

Используя формулы ( ) и ( ), получаем

j d	d		d
(~s ; ~sj 1) = (~sj ;~a1)			(~sj 1;~a1) = (j		1)'		(j		2)' = ';

( )

любые два последовательных суммарных вектора ~sj è ~sj 1 повернуты один относительно другого на один и тот же угол '.

 A0Aj Aj 1 углы при вершинах A0, Aj è Aj 1 равны соответственно ', (j 1)' и (180 j'): По теореме синусов применительно к A0Aj 1Aj имеем

sin '	=	sin(j 1)'	=	sin j'	;
a		sj 1		sj

откуда и следует формула (1.61).

2. Найдем проекцию суммы векторов ~a1 + ~a2 + + ~an = ~sn на ось, составляющую угол с вектором ~a1. Воспользуемся определением проекции вектора на ось (1.56), свойством (1.54), формулами (1.61) и ( ). В результате получим

	cos + cos(	+ 2') + +	sin n'
	+ cos [	+ 2'(n 1)] =		cos [ + (n 1)']: (1.62)
			sin '

50	Глава 1. ОСНОВНЫЕ СВЕДЕНИЯ ИЗ АЛГЕБРЫ
Из формулы (1.62) следуют равенства:
				sin n'		cos n';	(1.63)
cos ' + cos 3' + + cos [(2n 1)'] =					sin '
1 + cos 2' + + cos [2(n 1)'] =			sin n'		cos(n 1)'; (1.64)
			sin '
		sin n'
sin + + sin [ + 2'(n 1)]= sin ' sin [ +(n 1)'];(1.65)
					sin2 n'		(1.66)
sin ' + sin 3' + + sin [(2n 1)'] = sin ' ;
		sin n'		sin(n 1)';			(1.67)
sin 2' + + sin [2(n 1)'] = sin '
cos	+ cos h	+ 2n i + + cos h	+	2(n 1)		i = 0;	(1.68)
					n
	+ sin h	2		2(n 1)		i = 0:
sin		+ n i + + sin h	+		n		(1.69)

Формулы (1.63)-(1.67) получаются из (1.62) в результате подстановок: = ', = 0, = =2; = ' =2; = =2: А соотношения (1.68) и (1.69) отражают свойство замкнутого многоугольника, когда ' = =n и, следовательно, sn = 0.

Задачи

26.Используя определение проекции вектора на ось, найти значения sin ' и cos ' для следующих значений угла ' : 0 ; 30 ;

45 ; 60 ; 90 ; 120 ; 135 ; 150 ; 180 :

27.Используя результаты, полученные в примере 18, доказать формулы для суммы и разности тригонометрических функций:

2

2

sin + sin =

2 sin

+

cos

;

(1.70)

2

2

sin

sin =

2 cos

+

sin

;

(1.71)

2

2

cos + cos =

2 cos

+

cos

;

(1.72)

2

2

cos

cos =

2 sin

+

sin

:

(1.73)

Ÿ7. Вектор в ортонормированном базисе

7.1.Координаты вектора в ортонормированном базисе. Если в качестве базиса трехмерного пространства