Вопрос №1. Физическая величина свойства и единства измерения физических величин.

Физической величиной называется такое свойство материальных объектов, которое подлежит количественному измерению

Физическая величина определяется ее родом (масса, длина, эл. ток, сопротивление), а так же величиной (некоторой цифрой) определяемой количество единиц данной физической величины.

Для осуществления единства измерения физической величины существует определенные системы единиц этих величин с законами, правилами пересчета одной и той же физической величины в разных системных единицах.

В настоящее время рекомендовано к употреблению единичная международная система или СИ.

Каждая систематическая единица подразделяется на основные единицы и производные, которые получаются в результате определения комбинации основных физических единиц системы.

К основным единицам СИ относятся:

Кг, м, с, А, Кн

В понятие физической величины входит истинное , измеренное и действительное значения.

Истинное значение величины является объективной реальностью независящей от наблюдателя и найти точное значение величины практически не возможно, поскольку сам измерительный инструмент или средства измерения неизменно вносят погрешность.

Действительное значение физической величины – это такое ее значение, которое позволяет приблизится к истинному значению этой величины с наперед заданной точностью.

Измеряемое значение величины – количество единиц данной физической величины в процессе ее однократного измерения.

Параметрами физической величины называются такие ее характеристики, которые количественно отражают те или иные свойства физической величины.

Вопрос №2. Измерения. Шкалы измерений. Классификация измерений.

Измерение физической величины тесно связано с понятием шкал измерений. Имеется 4 типа шкал измерения:

1. наименований

2. порядка

3. интервалов

4. отношений

1. основано на предписанному объекту цифрах не имеющих отношения к количественному значению данной физической величины и указывающих лишь на принадлежность объектов физических величин одного и того же рода.

Пример: R1, R2, R3… R15

2. (натуральная шкала) – предполагает упорядочение объектов относительно какого-либо определенного свойства в порядке возрастания или убывания.

Сама процедура разделения называется ранжирование.

При этом имеются некоторые опорные точки, выраженные в единицах физической величины, позволяющие проводить такое ранжирование в сторону убывания или возрастания.

3. Предполагает измерение интервалов значений физической величины выбранных искусственным образом, т.е. достаточно произвольно определяется начальная и конечная точи интервалов измерения физической величины.

Содержит как положительные так и отрицательные значения.

4. в которых начальная точка совпадает с естественным нулем данной физической величины.

Классификация:

1. по способу нахождения физической величины.

Измерения можно разделить на :

1. прямое измерение (осуществляется самим наблюдателем с помощью измерительного прибора или устройства)

2. косвенное измерение (позволяет определить значение физическое величины по известной аналитической зависимости или формуле)

3. совместной измерение (цель является установление аналитической зависимости одной физической величины от другой физической величины)

в процессе проводится независимое измерение как одной величины так и другой. В результате измерений строится таблица и по ней строится поле экспериментальных точек в соответствующем масштабе. По этому полю подбирается некоторая известная функция, которая бы наилучшим образом описывало данное поле точек.

4. Совокупное измерение (проводится несколько одноименных величин при котором искомое значение находится решением системы уравнений, полученной при прямых измерениях различных сочетаний этих величин)

2. по режиму проведения измерения:

1. статические (в процессе измерения сама величина не меняется)

2. динамические (в процессе которых происходит изменения самой величины)

3. по роду измеряемой величины (оптическая, механическая, электрическая, акустическая).

Вопрос № 3. Средства измерений

К СИ относятся: измерение меры физических величин, измерительные приборы, которые подразделяются на аналоговые и цифровые (измеренная информация представляется в виде отчета по шкале прибора и на цифровом табло); измерительные установки в котором измерительная информация также фиксируется наблюдателем; измерительные комплексы, в которых измерительная информация не фиксируется самим наблюдателем, а используется для контроля каких – то физических процессов, либо для ее обработки и хранения.

Вопрос № 4. Погрешность измерения и их классификация

Обозначим измеряемую физическую величину через Х (самой разнообразной природы, может подвергаться измерениям однократно или многократно).

Абсолютная погрешность однократного измерения (Δ) называется разница между измеренным и истинным значениям физической величины

(1)

поскольку Хист как правило не известно, то в (1) вместо Хист подразумевается близкое к нему значению поддающееся определению опытным путем или действительное значение измеряемой величины Хд

Относительная погрешность (δ) -

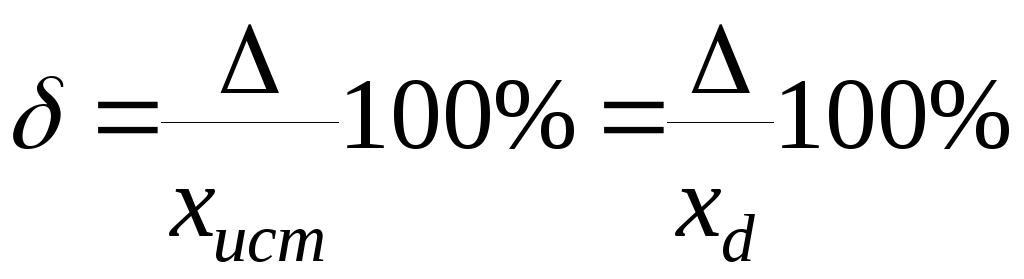(2)

Приведем несколько классификаций погрешности:

1. по характеру проявления по времени (можно подразделить на две группы: систематические и случайные)

1. Систематические – зависят от времени, и повторяются, сохраняя свое значение от одного измерения к другому и поэтому существуют трудности с их выявлением.

2. Случайные – проявляются в небольшом изменении значения измеряемой величины в ту или иную сторону и возникают в результате одновременного воздействия множественных факторов (для выявления и учета разработаны и применяются такие разделы математики как теория вероятности, теория ошибок, математическая статика и др.)

Систематическая погрешность подразделяется на:

• Приборная погрешность

• Методическая погрешность (различные методики)

• Личностная погрешность (человеческий фактор) (связан промах или сильное (глубокое) отклонение значения измеряемой величины, по сравнению с другими значениями измеряемой величины Х в процессе проведения измерения в одних и тех же внешних условиях).

По условию возникновения систематическую подразделяют на основную и дополнительную.

Дополнительная к основной возникает когда изменяется внешние условия проведения измерения (температура, давление, влажность среды)

Вопрос № 5. Систематические погрешности. Их обнаружение и исключение

Систематические – зависят от времени, и повторяются, сохраняя свое значение от одного измерения к другому и поэтому существуют трудности с их выявлением.

Систематическая погрешность подразделяется на:

• Приборная погрешность

• Методическая погрешность (различные методики)

• Личностная погрешность (человеческий фактор) (связан промах или сильное (глубокое) отклонение значения измеряемой величины, по сравнению с другими значениями измеряемой величины Х в процессе проведения измерения в одних и тех же внешних условиях).

По условию возникновения систематическую подразделяют на основную и дополнительную.

Дополнительная к основной возникает когда изменяется внешние условия проведения измерения (температура, давление, влажность среды)

В отличии от случайной погрешности не существует единой универсальной методики выявления и исключения систематической погрешности.

В простейшем случае проведения измерения с помощью одного прибора систематическую инструментальную погрешность можно определить по классу точности измерительного прибора:

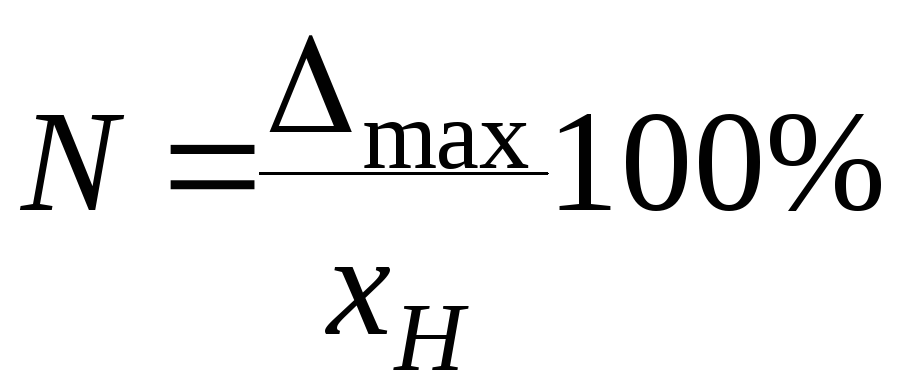
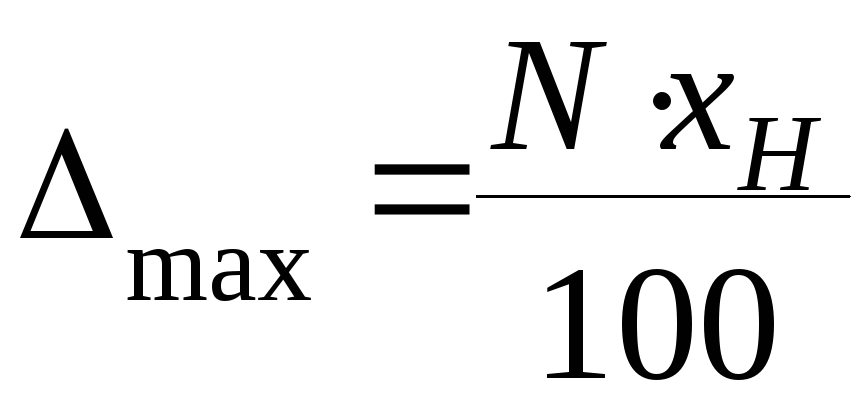
из формулы следует, что чем меньше номинальное значение измеряемой величины тем больший вклад вносит инструментальная погрешность.

Вопрос №6. Случайные погрешности измерения. Их метрологические характеристики.

Случайные – проявляются в небольшом изменении значения измеряемой величины в ту или иную сторону и возникают в результате одновременного воздействия множественных факторов.

Случайные погрешности наряду или вместе с систематической наблюдаются в процессе проведения серии прямых равноточных измерений физической величины Х, когда результатом измерения является ряд близких значений Хi измеряемой величины Х.

Основной характеристикой случайной величины измеренного значения Х, усредненное по серии значение измеренной величины, погрешность измерения и др., является функция плотности вероятности этой величины или же закон ее распределения.

f(x) – некоторая математическая формула где х – сама случайная величина.

Гистограмма получающиеся следующим образом: в процессе измерения выявляется некоторое максимальное и минимальное значение некоторой величины. Весь интервал разбивается на п – частей и выявляется частота попадания значений измеряемой величин в тот или иной интервал.

В результате строится график:

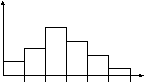
7. Гистограмма распределения случайной величины. Ф-я плотности вероятности

её распределения.

Пусть производится многократное измер–е физ. вел. х в одних и тех же внешних условиях. При этом истинное знач-е вел-ны х (Х_ИСТ) не известно, и в процессе измерений нах-ся оценка Х_ИСТ – Х_ДЕЙСТВ, которая при увеличении числа измерений приближается к её ист-му значению. В процессе измер-й появляются знач-я Х_min ≤ Х ≤ Х_max При этом произв-ся некоторое количество измерений (напр-р, п =50)

Нах-ся интервал измер-я Х_max- Х_min = ∆Х , который разбивается на К – равных промежутков (напр-р К = 5)

Опред-ся число знач-й измер-ой вел-ны, попадающих в каждый интервал, и строится таблица:

nk	5	12	18	11	4	…..
nk/n	0,1	….	…	..	..	..

Строится гистограмма случ вел-ны Х

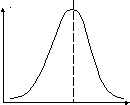
Из рис1 видно, что частота измер-х значений Х достигает максимума в районе середины, что указывает на то ,что где-то в приделах этого прямоугольника находится истинное значение измеряемой величины.

Появление измеряемых значений Х , как в сторону уменьшения, от центра распределения(влево), так и в строну увеличения значений Х (право), снижается

Частота появления тех или иных измеренных знач-й Х определяет вероятность получения тех или иных измер-х значений.

При увеличении числа интервалов n_K ступенчатая ф-я рис1 может быть заменена некоторой плавной кривой f(x), кот-я наз-ся ф-цией плотности вер-ти появление тех или иных измер-х знач-й величины Х, а dP = f(x)dx – вероятность показания тех или иных измеренных значений вел-ны х в тот или иной интервал dx

При этом поведение ф-и f(x) практически повторяет ход гистограммы.

Явный вид функции f(x), т.е. вер-ти появления того или иного значения х в процессе измерения называется законом распределения случайной вел-ны х.

Наиболее вер-е значение –Х₁ - max f(x).

Знач-е Х₁ – мода распределения.

Наблюдаются различные виды ф-и f(x) или разл-е виды з-ков распред-я Х

Законы

р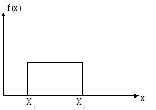авномерное распр-е вероятности появления случ-х вел-п в некотором ограниченном интервале х (отсутсвуетмода)

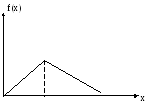
Т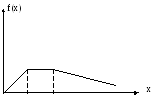реугольный закон распределения случайной величины

Трансцеидальный закон распределения

Нормальный закон распределения

Наиболее часто проявляется при поведении серии прямых равноточных измерений одной и тоже величине х при большом количестве измерений(п ≥ 15) п ≥15 – серия большой выборки п < 15малой выборки

Особенности закона норм распределения

1) имеется явно выраженный центр (мода) закона распределения

2) ход кривой ф-и f(x) симметричен относительно центра распределения, т.е вер-ть появления измеренных значений величины х, симметричных относительно центра, становится одинаковой при большом числе измерений

3)Рассеяние измеренных значений относительно центра уменьшается с уменьшением пар-ра σ, где

σ – среднеквадратичное отклонение (СКО) f(x), опред-ся по результатам измер-й

Вер-ть для данного значения σ появления измеренного знач-я Х в интервале dx численно равна заданной на площади квадратной трапеции, делённой на площадь фигуры ограниченной кр-й распределения и осью Х(вер-ть≤1) реал-е значение вер-ти события(вер-ть достоверн события) = 1

Ф-ия f(x) нормируется на 1-цу так называемым углом нормировки

(1)

Равенство (1) показывает, что любое измеренное значение величины х в интервале (-∞ ;+∞) явл-ся событием достоверным, вер-ть которого=1

Интеграл имеет геометрический смысл площади отсюда следует, что площади ограниченные кривыми норм. закон распред. для разных σ, одинаковы и равны 1

Вопрос №8. Характеристики закона распределения случайной величины (мода, Д, σ).

Явный вид функции, графиком которой является кривая нормального распределения, получил немецкий математик Гаусс, поэтому закон нормального распределения Х называется законом Гаусса, который имеет вид:

(1)

Х0 – центр распределения

Употребляется также математическое ожидание случайной величины.

f(x) определяет количественные характеристики данного распределения или ее момент mi момент к – того порядка определяется по формуле:

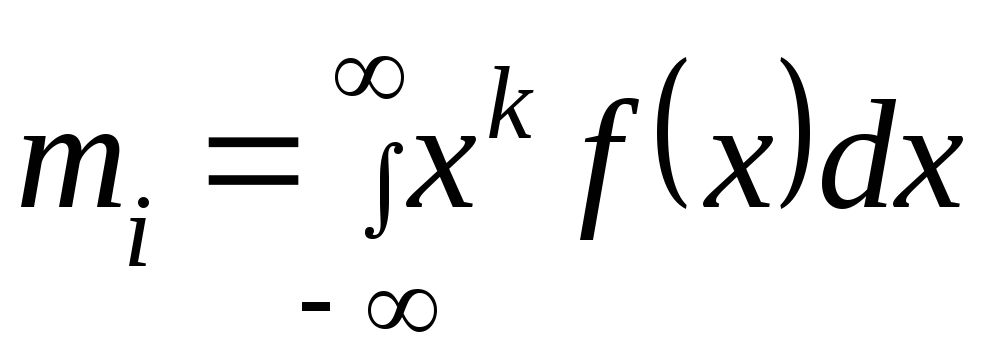(2)

Момент случайной величины Xi определяемый симметрично относительно начала координат называется начальным моментом. Наиболее важным моментом является начальный момент первого порядка, которое определяется математическое ожидание случайной величины х. 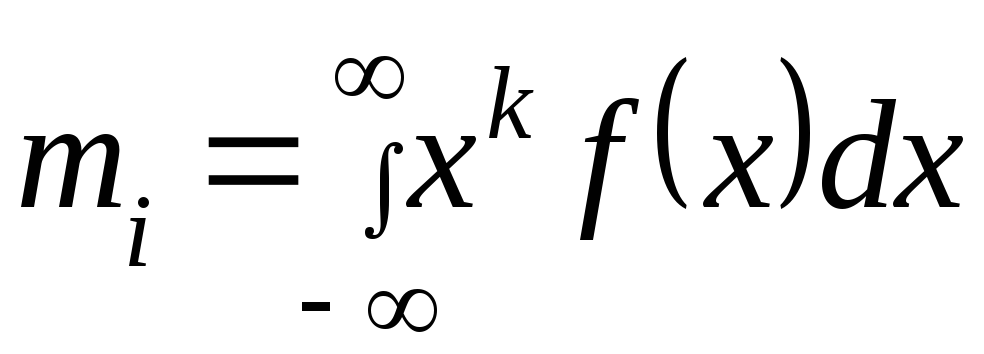(4). Кроме начальных моментов заданный закон распределения определяет центральные моменты К – го порядка по формуле:

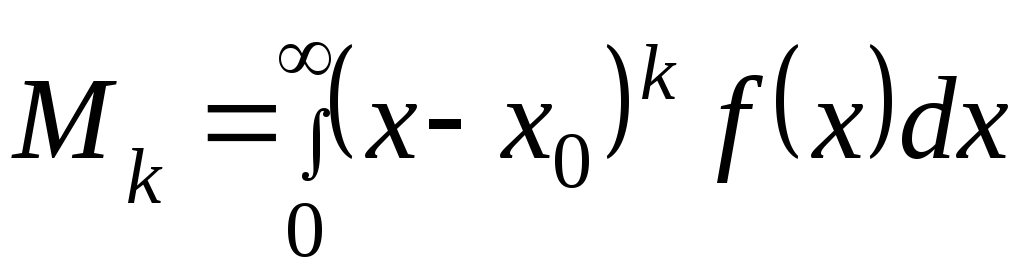(3)

Х0 – центр распределения, который для нормального распределения совпадает математическим ожиданием случайной величины х и определяется по формуле:

х0=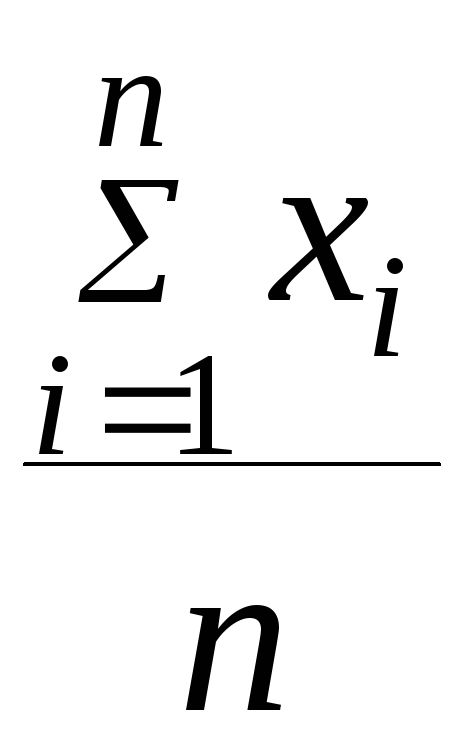 (средне арифметического) (4)

Само математическое ожидание также является случайной величиной и зависит как от измеренных значений, так и от числа измерений.

Считается, что центр значения ожидания имеет положительное значение. Наиболее важным является центральный момент второго порядка

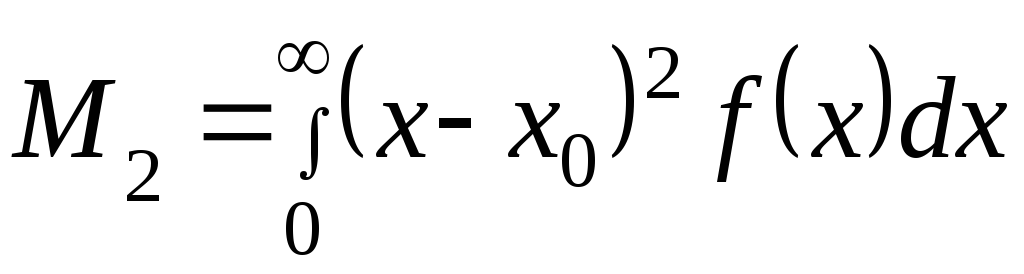(5)

этот момент называется дисперсией Д случайной величины и характеризуется степенью отклонения измеренного Х от центра распределения, т.е. от математического ожидания.

Размерность Д равна размерности квадрата измеряемой величины Х. наряду с Д вводится квадратный корень из этой величины, т.е.:

(6).

Выражение для σ в случае нормального распределения с использованием (5) и (6):

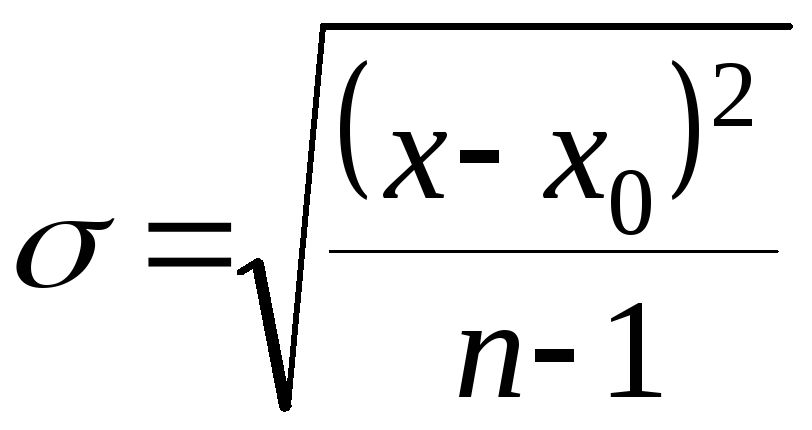
Вопрос №9. Закон распределения абсолютной погрешности прямого измерения.

Абсолютной погрешностью i-ого измерения в серии прямых измерений называется величина определяемая как разность между измеренным значением и средне арифметическим значением Х, которое для нормального закона распределения определяется по формуле:

.

Причем Δi может появляться, как со знаком «+» так и со знаком «-»

Само арифметическое значение является величиной случайной, зависящей от числа измерений в серии, степень разброса которой характеризуется параметром определяемой по формуле:

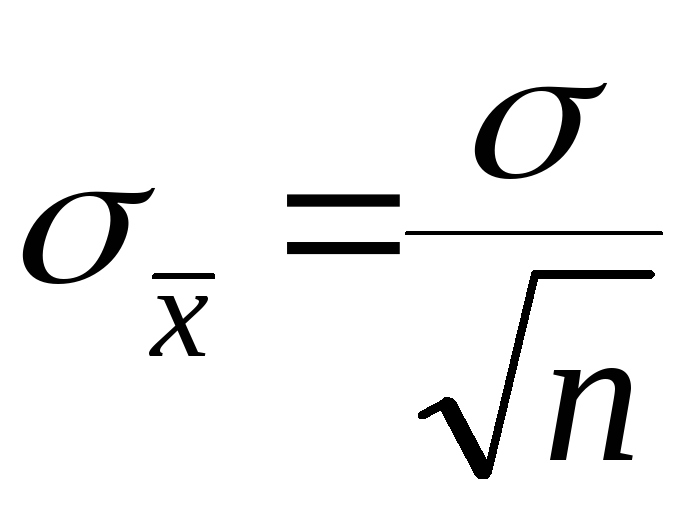, т.е. разброс средне арифметического относительно центра распределения в раз меньше, чем разброс относительно центра самой измеренной величины:

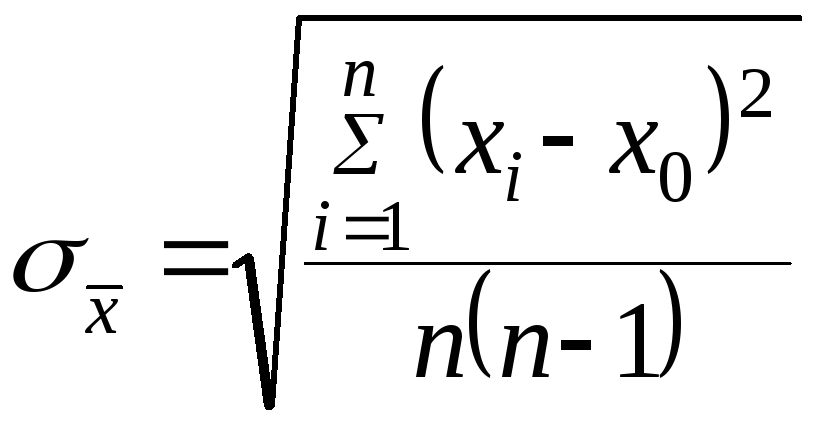
Абсолютная погрешность в серии прямых измерений также является случайной величиной подчиняется такому или иному закону распределения.

Нормальный закон для распределения абсолютной погрешности имеет вид:

.

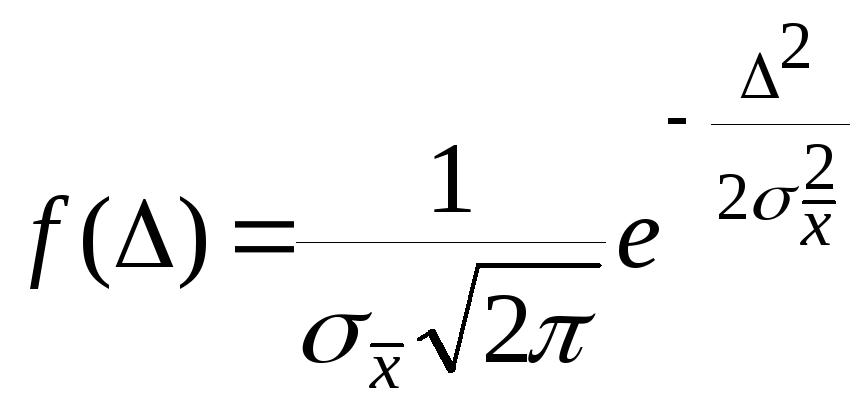Если для самой случайной величины Х имеются некоторое ее наибольшая вероятность появления, то наибольшая вероятность значения абсолютной погрешности прямых измерений является ее значение равное 0.

- среднеарифметическое от средне квадратичного отклонения.

Вопрос №10. Интеграл вероятности. Доверительная вероятность и доверительный интервал.

Установлено, что при большом числе измерений в серии (большая выборка) закон распределения случайной величины, чаще всего сводится к нормальному или закону распределения Гаусса.

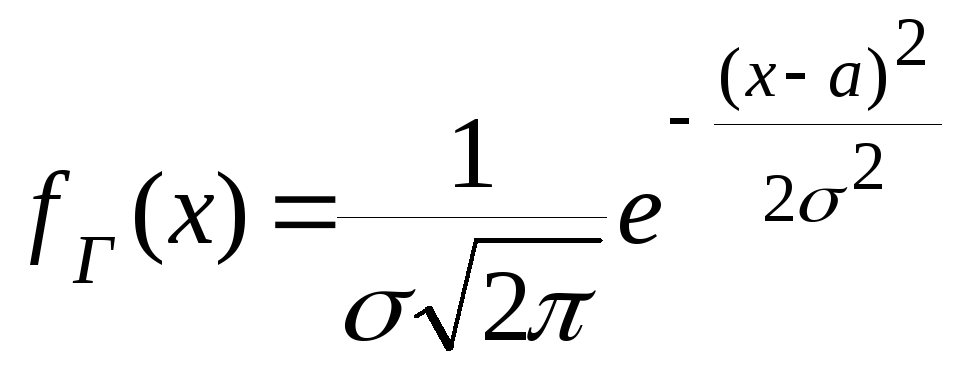
.(1)

В частности можно предположить границы этого определенного интеграла, как 0 и ∞

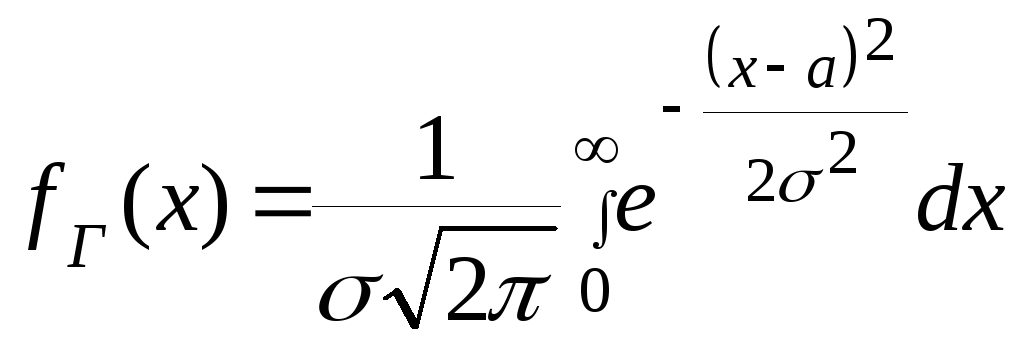(2)

функция распределения f(x) имеет вероятностный смысл, а любое значение f(x) распределяет некоторое значение вероятности его появления. При этом вероятность появления значения Х в интервале от Х до Х+dХ (dP).

, (3) тогда вероятность появления значения Х в некотором конечном интервале ее изменения найдется по формуле.

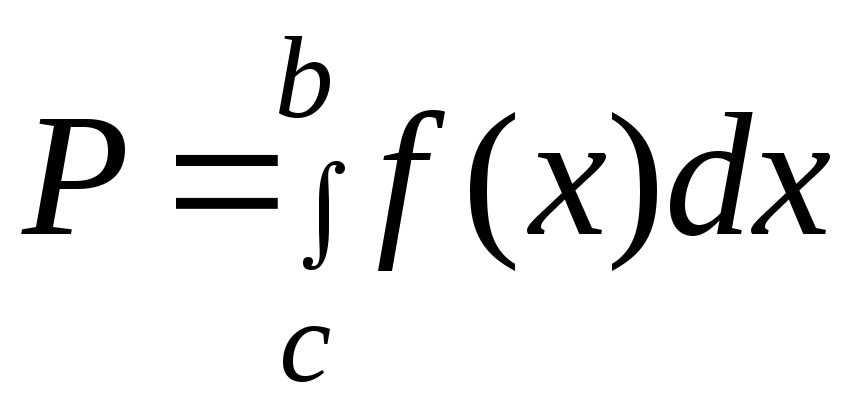(4)

правая часть формулы называется интегралом вероятности, а левая доверительной вероятностью.

В теории вероятности максимальное значение вероятности не каждой случайной величины (ее достоверное значение) называется доверительным значением.

Вероятность того, что значение измеряемой величины Х лежит в пределах от 0 до ∞, является событие достоверное с вероятностью равной 1.

Математически это утверждение формируется в виде условия нормировки.

(5)

поскольку функцияf(x) нормирована условием (5), то интеграл (4) должен быть <1.

Максимальное значение Δ (абсолютной погрешности) в серии прямых измерений соответственно с некоторой вероятностью ее появления (доверительной вероятности) называется границей доверительного интервала или доверительным интервалом.

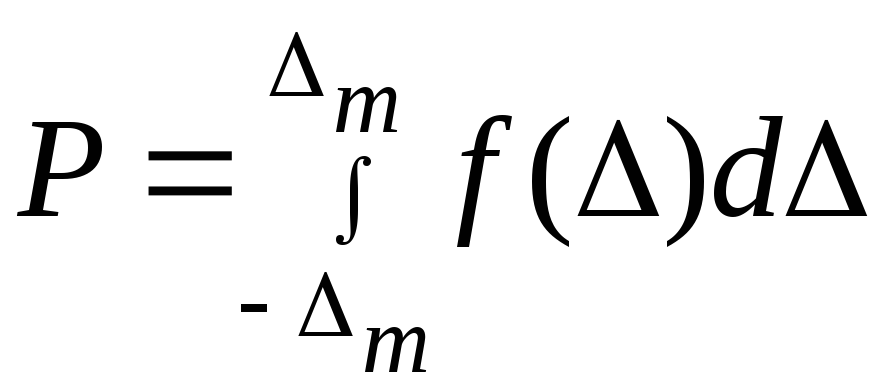, (6)где Δi – определяет некоторое произвольное заданное максимальное значение абсолютной погрешности измерений. Геометрически интеграл (6) определяется как площадь криволинейной трапеции.

Вопрос №11. Интеграл Лапласа. Формула доверительного интервала. Критерии выявления промахов.

Предположим, что число измерений в серии велико, при этом закон распределения самой случайной величины f(x), а также закон распределения f(Δ) – стремится к закону Гаусса.

Поскольку кривая нормального распределения симметричная интегралу после подстановки в него f(x) Гаусса можно представить в виде:

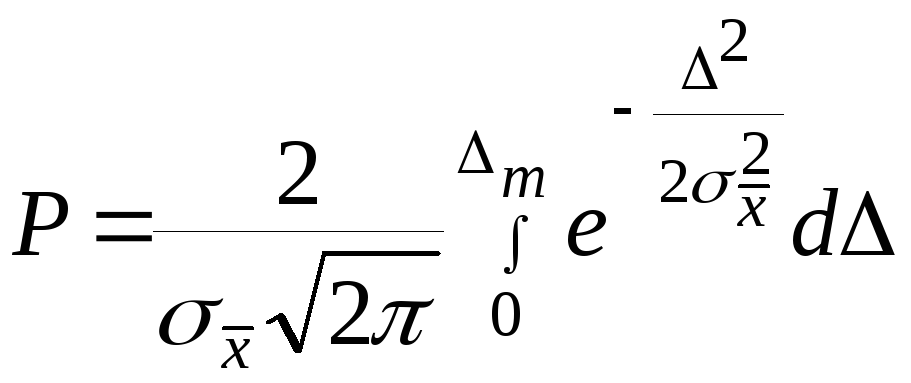(1)

сделаем в интеграле (1) замену переменной, т.е. введем некоторую безразмерную величину:

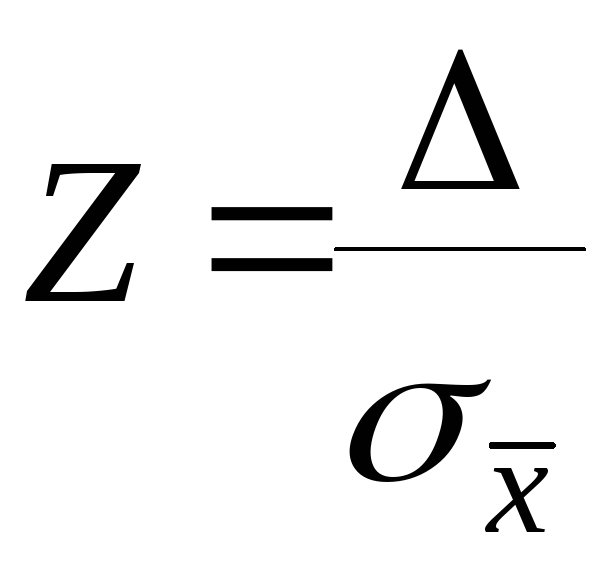(2)

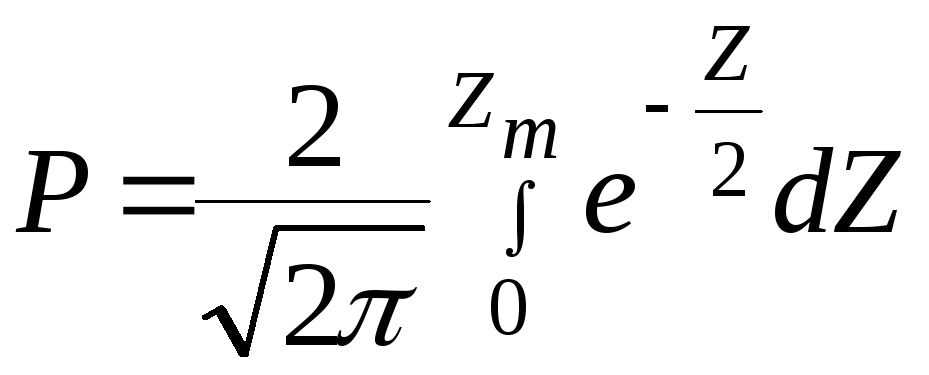
(3)

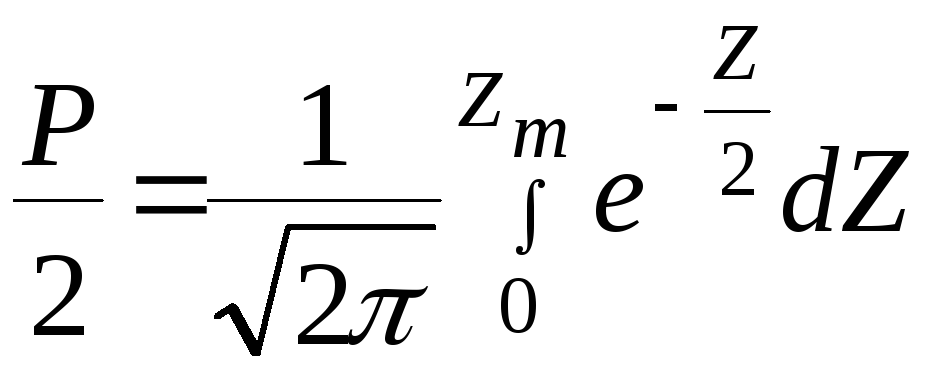
Вывод: при нормальном законе распределения f(Δ) граница доверительного интеграла, т.е. максимальное значение погрешности отклонения от среднего арифметического определяется по формуле (3) при этом Zm находится по таблицам интеграла Лапласа для заданного значения половины доверительной вероятности. Сам график интеграла Лапласа, т.е. функция имеет вид:

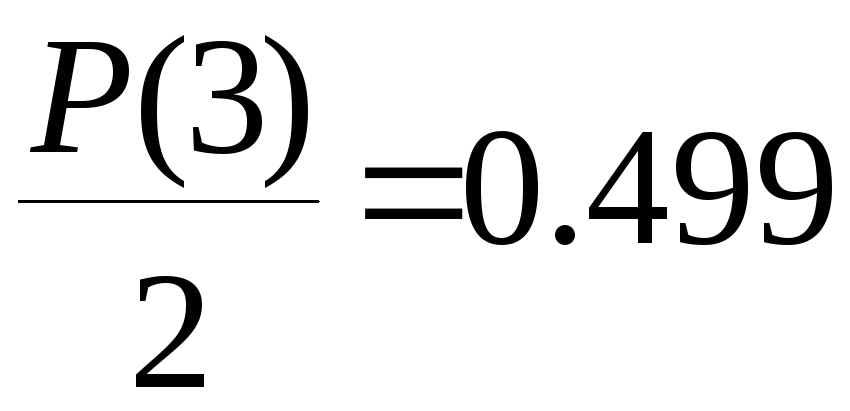
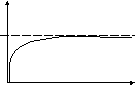(4)

формула (4) показывает, что значение абсолютной погрешности соответствует вероятности равной 0,499

Интервал появления вероятности погрешности измерения Δ:

.

Вопрос № 12. Статическая обработка серии большой выборки прямого измерения.

При большой выборке (п ≥ 15), как показывает опыт, измеряемое значение Х обычно подчиняется нормальному закону распределения относительно некоторого максимума или моды функции распределения.

Мода измеряемой величины, как наибольшее вероятное ее значение является оценкой истинного значения величины Х или действительным ее значением в данной серии.

Однако, при обработке измерений, мода физической величины не определяется, а принимается, что при выполнения условия 1 (п ≥ 15) нормальным законом распределения выполняется.

За результат статическим обработками принимается нахождения математического ожидания физической величины для чего применяется следующий алгоритм вычислений.

1. Находится среднее арифметическое по серии

2. Находится абсолютная погрешности измерений

при этом Δ входит, как со знаком «+» максимум и с «-»

3. Проверяется нормальность закона распределения Δ. Известно, что модой нормального распределения f(Δ) является 0.

Поэтому сумма всех Δ-й.

4. Если f(Δ) не подчиняется закону Гаусса, то полученное Δi проверяется промахи.

5.

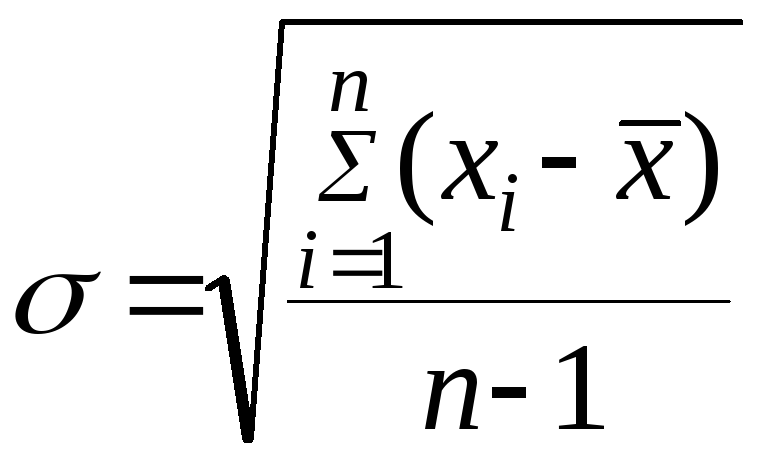
6.

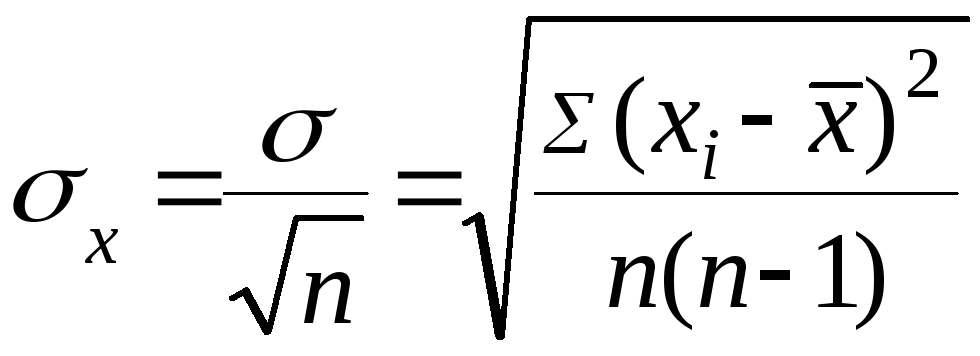
7. Если некоторая Δi является промахами, то они исключаются из серии измерений (возвращаемся к пункту 3). В результате исключения промахов: . После процедуры 5 и 6 повторяются.

8. для вычисления доверительного интервала Δm, необходимо задаться значением доверительной вероятности. Типичным значением р является значение вероятности равной 0,95. задавшись значением р мы утверждаем, что с 95% вероятностью все значения погрешности Δi войдут в доверительные границы – искомому Δi.

С помощью таблиц интеграла Лапласа находятся значение верхнего предела интеграла Лапласа Zn, при этом, как было показано границы доверительного интервала .

9. (математическое ожидание).

Δm – максимальное значение абсолютной погрешности, имеющей случайных характер.

Однако, кроме случайной погрешности, может присутствовать и не исключаемая систематическая погрешность, оцениваемая своим максимальным значением или границей (НСП).

В теории погрешности 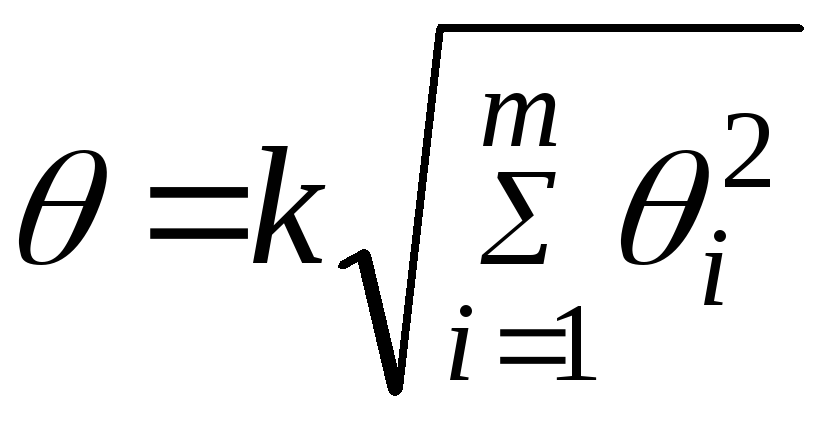(θ - тетта), где

- не исключенная НСП соответствующего номера.

В самом простейшем случае, если исключить личностную погрешность, выбрана самая удачная методика измерений и саамы измерения проводятся одним единственным прибором, то в этом случае граница НСП определяется классом точности измеряемым прибора по формуле.

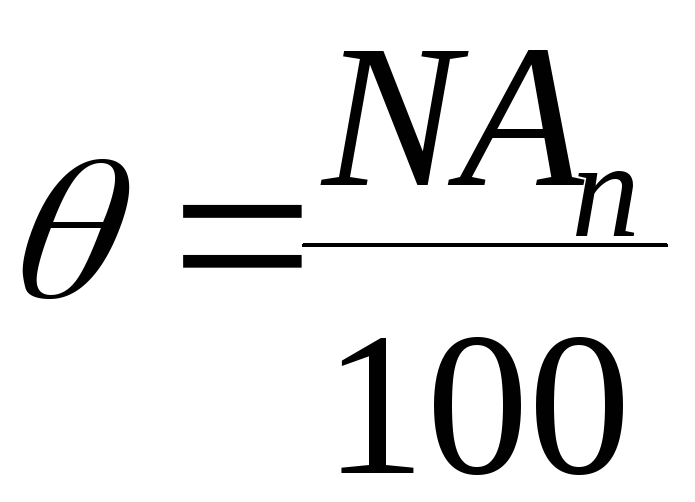- класс точности.

При этом коэффициент К зависит от доверительной вероятности. При р=0,5, К=1,1.

Найдя θ, поступают следующим образом:

А) Если , то не исключена систематическая погрешность (НСП) пренебрегают, т.е погрешность считают частично случайной с максимальным значением Δm.

Б) Если 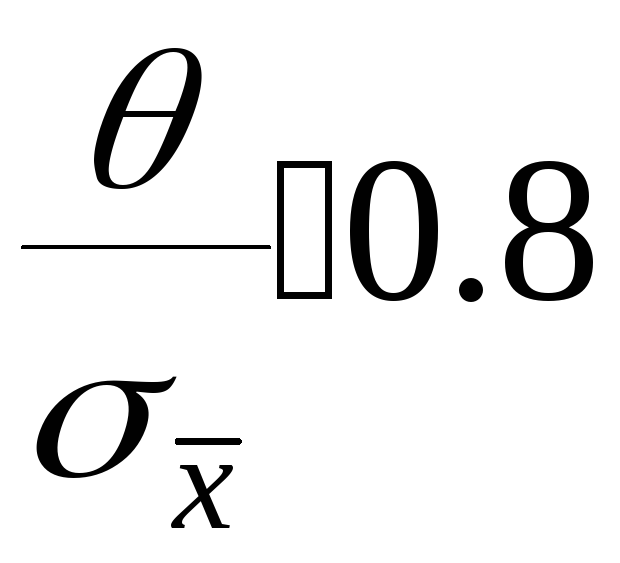, то пренебрегают случайной ошибкой и в этом случае границы общей погрешности принимают θ.

Вопрос №13. Статическая обработка серии малой выборки.

Серия малой выборки n<15.

С уменьшением числа измерений в серии закон распределения самой случайной величины f(x), а также закон распределения Δ все более отклоняются от нормального.

Английский математик Госсет нашел вид этого распределения основным свойством которого является то, что при п→∞,

Используя полученную формулу, Госсет построил таблицы по типу таблиц интеграла Лапласа, по которым находится верхний предел интеграла вероятности с подынтегральной функцией . Значение верхнего предела обозначается буквой t, значение которой находится по таблице при заданной значение р и п.

t – называется коэффициентом Стьюдента, которой используется для нахождения доверительной границы случайного характера.

.

Весь остальной порядок нахождения математического ожидания остается таким же, как и в нормальном случае.

Вопрос №14. Погрешность косвенного измерения.

Измерение называется косвенным, если результатом такого измерения насчитываются по известной математической формуле.

Как правило, абсолютная погрешность измеряемой физической величины имеет ту же размерность, что и сама величина и является величиной малой, если она не является промахом.

Т.е по смыслу абсолютная погрешность измерения приближается к понятию дифференциала величины Х, т.е. к бесконечно малому отклонению от истинного значения.

.

Однако эта формула имеет недостаток, что частные производные могут иметь различные знаки.

В теории ошибок доказывается, что складывается не из самих погрешностей, а из их квадратов, т.е. дисперсии случайной величины.

Поэтому абсолютная погрешность косвенного измерения определяется по формуле:

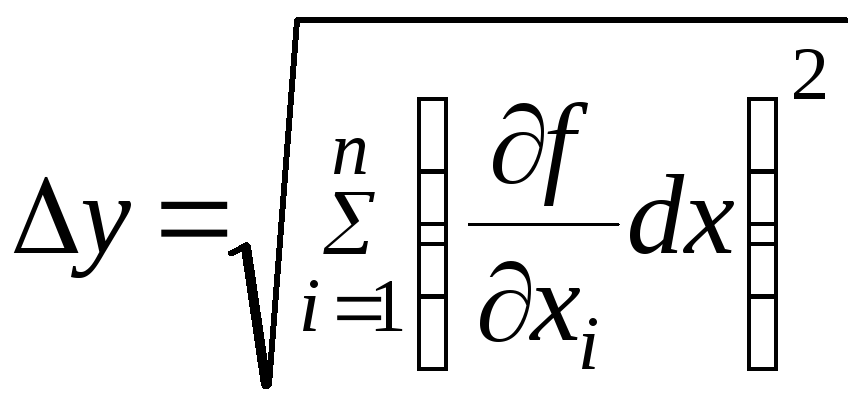
Вопрос №15. Задача совместного измерения. Функция аппроксимации.

В результате проведения совместимого измерений определяется прямым измерением искомая величина Y. Так и определяется другая измеряемая .(1)

-неявная функция одной величины Х (2)

yi	xi
y1	x1
y2	x2
…	…
yn	xn

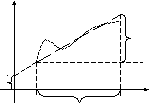О сновной задачей совместного измерения является подбор такой математической зависимости (2) или (1), чтобы она наилучшем образом описывала экспериментальное поле точек.

А именно в качестве критерия выбирается минимальное отклонение экспериментальных точек от теоретической кривой. Для этого применяется различные известные математические зависимости – функции аппроксимации.