|
ТЕМА 6_Бак |
|
НЕСИНУСОИДАЛЬНЫЕ ТОКИ |
|
6. Периодические несинусоидальные сигналы 6.1. Основные понятия 6.2. Разложение в ряд Фурье 6.3. Расчет несинусоидальных режимов в мгновенных значениях 6.4. Метод эквивалентных синусоид 6.5. Высшие гармоники в однофазных цепях 6.6. Трехфазные цепи с несинусоидальными ЭДС, напряжениями и токами 6.7. Высшие гармоники в трехфазных цепях
|
6. Периодические несинусоидальные сигналы
6.1. Основные понятия
Причины возникновения несинусоидальных режимов
Причиной возникновения несинусоидальных режимов в линейных электрических цепях является несинусоидальностьЭДС и напряжений источников:
ЭДС синхронных генераторовсодержат высшие гармоники вследствие наличия зубцов и насыщения магнитопровода;
вторичные источники:
выходное напряжение выпрямителя содержит постоянную составляющую и пульсации;
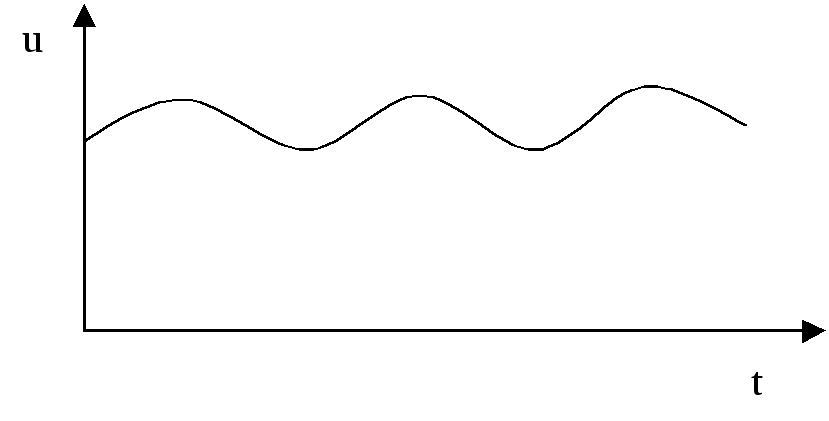
выходное напряжение релаксационных генераторов– мультивибраторов, генераторов пилы и т. д. – имеет прямоугольную, треугольную, трапецеидальную и другие формы.
Принципы анализа цепей с несинусоидальными напряжениями и токами
В основе анализалинейных электрических цепей с несинусоидальными напряжениями и токами лежат:
представление несинусоидальных периодических напряжений и токовв видетригонометрического ряда Фурье;
применение принципа наложения для расчета мгновенных и действующих значений напряжений и токов;
6.2. Разложение в ряд Фурье
Из курса математики известно, что любую периодическую функцию (e,u,i), удовлетворяющую условиям Дирихле, можно разложить в тригонометрический ряд Фурье.
Условия Дирихле:
Функция должна иметь за период конечное число разрывов первого рода.
Функция должна иметь за период конечное число максимумов и минимумов.
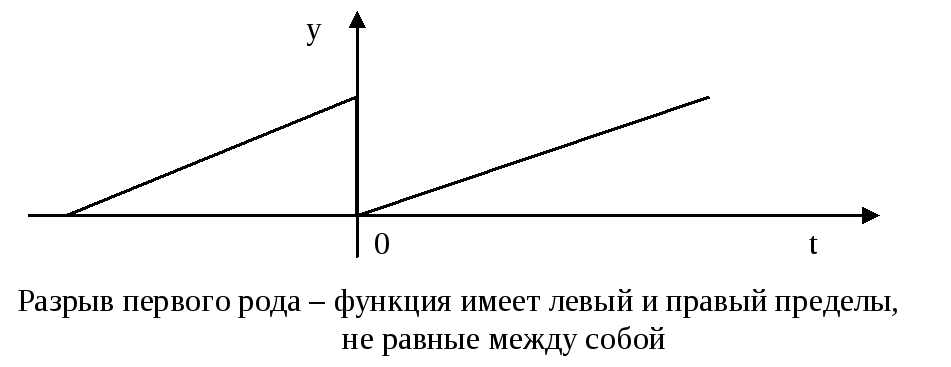
В физически реальных электротехнических и электронных цепях все периодические функции условиям Дирихле удовлетворяют.
Разложение в ряд Фурье, если функция
задана аналитически
,
где 
– постоянная составляющая;
– амплитуда синусной составляющейк-й
гармоники;
–
амплитуда косинусной составляющейк-й
гармоники.
Коэффициенты можно записать в другой форме:
;
;
.
Часто используют другую форму записи разложения Фурье.
Если полагать, что
и
,
то для любой гармоники
,
где 
,
.
В результате:
,
где 
–
постоянная составляющая;
– основная или первая гармоника, период
которой равен периоду самой несинусоидальной
функции;
– высшая гармоникак-го порядка.
В общем случае ряд Фурье содержит бесконечное число членов ряда, но на практике ограничиваются некоторым конечным их числом.
Разложение в ряд Фурье, если функция
задана графически
В этом случае определенный интеграл заменяют суммой конечного числа слагаемых.
С этой целью кривую разбивают на nравных интервалов и подсчитывают коэффициенты Фурье по приближённым формулам:
;
;
,
где 
–
номер интервала.
Разложение в ряд Фурье, если функция
существует в виде разности потенциалов
в электрической цепи
Коэффициенты разложения
и
определяют приборы –гармонические
анализаторыпутем подачи исследуемого
несинусоидального напряжения на зажимы
прибора.
В большинстве практических случаев пользуются разложениями, взятыми из справочников, учебников, монографий.
Свойства периодических несинусоидальных функций, обладающих симметрией
Еще до разложения по наличию того или иного вида симметрии можно предсказать наличие или отсутствие того или иного вида гармоник
кривая симметрична относительно оси ординат (симметрия I-го рода):
При разложении в ряд Фурье отсутствуют
синусные составляющие гармоник (
).
кривая симметрична относительно начала координат (симметрия II-го рода):
При разложении в ряд Фурье отсутствуют постоянная составляющая и косинусные составляющие.
кривая симметрична относительно оси абсцисс:
При разложении в ряд Фурье отсутствуют постоянная составляющая и четные гармоники.
Пример разложения:
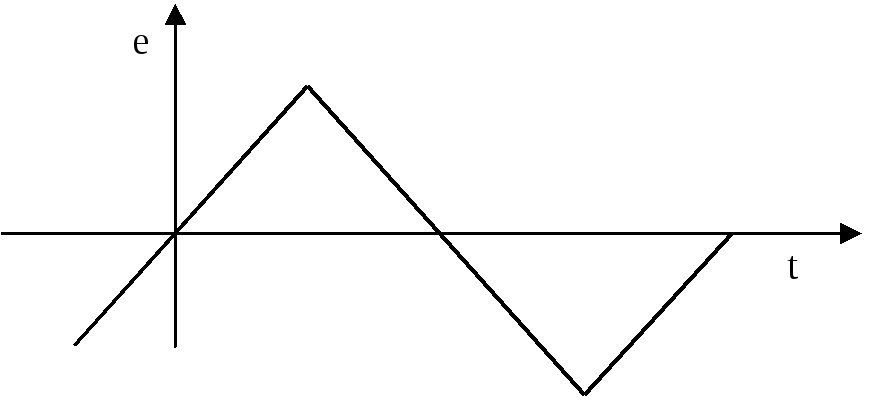
Симметрия относительно оси абсцисс и начала координат.