Zapiska_moya11

МИНОБРНАУКИ РОССИИ

Воткинский Филиал

федерального государственного бюджетного образовательного учреждения

высшего образования

“Ижевский Государственный Технический Университет им. М. Т. Калашникова”

(ВФ ФГБОУ ВО «ИжГТУ имени М.Т. Калашникова»)

Кафедра «Технология машиностроения и приборостроения

Контрольная работа

По дисциплине: «Теория автоматизированного управления»

Выполнил: студент гр. Б05-721-1зт О.В. Русанова

Проверил: к.т.н, доцент И. А. Давыдов

Воткинск,2016

Электрогидравлическая следящая система

с дроссельным управлением (станки с ЧПУ)

1. Исходные данные

№ вар.	ЭУ	ЭМУЭ		ГУ		ГИМ	ОС
	Кэу	Тэмуэ	Кэмуэ	Тгу	Кгу	Кгим	Кос
	-	с	мм/В	с	л/(мм с)	мм/л	В/мм
6	500	0,15	0,05	0,08	1,3	?	0,015

1.1 Принципиальная схема системы управления

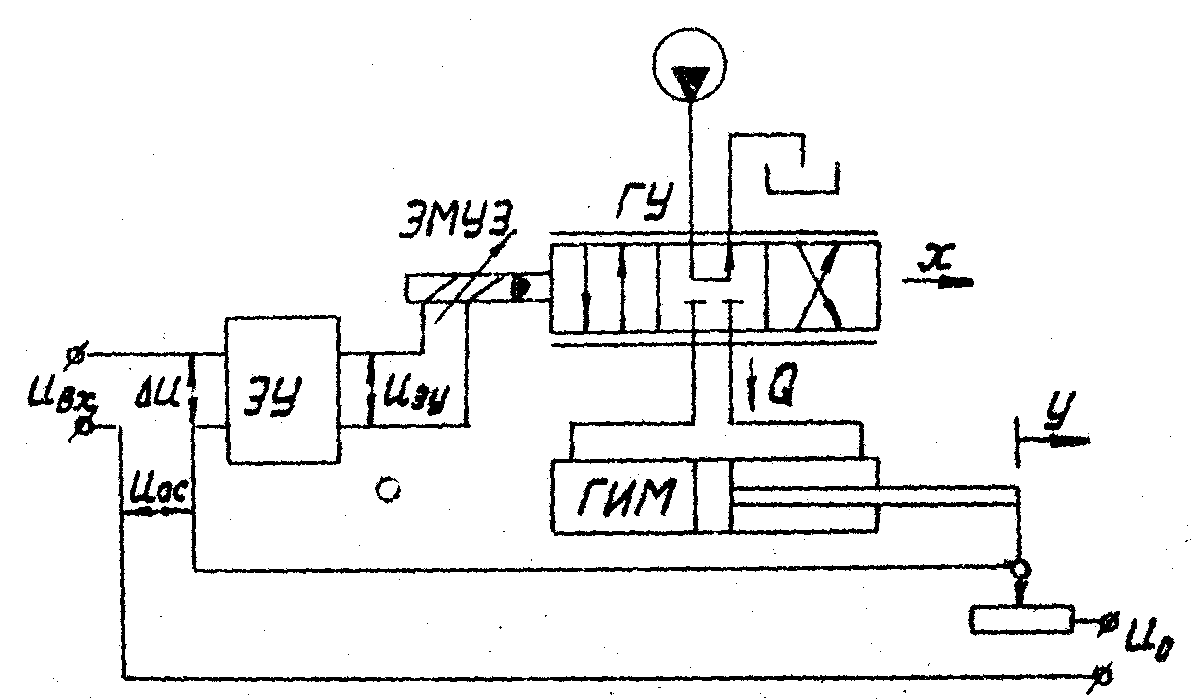
Рис. 1. Принципиальная схема САУ

Рис. 2. Структурная схема САУ.

1.3. Уравнения динамики элементов системы управления

Электронный усилитель (ЭУ):

(1)

где U_ЭУ – напряжение на выходе из электронного усилителя;

К_ЭУ – коэффициент усиления электронного усилителя;

ΔU – напряжение на входе электронного усилителя (рассогласование системы).

Электромеханический управляющий элемент (ЭМУЭ):

(2)

где Т_ЭМУЭ – постоянная времени ЭМУЭ;

х – смещение якоря ЭМУЭ;

К_ЭМУЭ – коэффициент передачи ЭМУЭ;

Гидравлический усилитель (ГУ):

(3)

где Т_ГУ – постоянная времени гидроусилителя;

Q – поток рабочей жидкости, направляемый в исполнительный механизм;

К_ГУ – коэффициент передачи гидроусилителя.

Гидравлический исполнительный механизм (ГИМ).

(4)

где y – смещение исполнительного органа;

К_ГИМ – коэффициент передачи ГИМ.

Обратная связь (ОС):

(5)

где U_ОС – напряжение на выходе ОС;

К_ОС – коэффициент передачи ОС.

1.4 Значения параметров элементов САУ

К_эу=500

Т_эмуэ=0,15 с

К_эмуэ=0,05 мм/В

Т_гу=0,08 с

К_гу=1,3 л/(мм∙с)

К_гим= ?

К_ос=0,015 В/мм

2. Анализ элементов системы управления

2.1. Типы элементов системы управления

Электронный усилитель (ЭУ) – Пропорциональное идеальное звено

Электромеханический управляющий элемент (ЭМУЭ)-

Пропорциональное инерционное звено

Гидравлический усилитель (ГУ) - Пропорциональное инерционное звено

Гидравлический исполнительный механизм (ГИМ)-

Интегрирующее идеальное звено

Обратная связь (ОС)- Пропорциональное идеальное звено

2.2. Переходные характеристики элементов

Э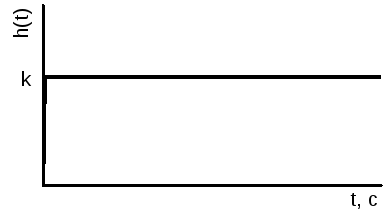лектронный усилитель

Электромеханический управляющий элемент

Гидравлический усилитель

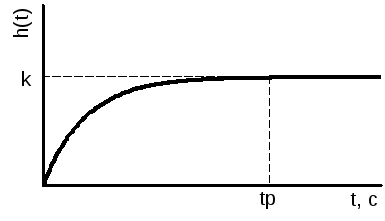
Гидравлический исполнительный механизм

Обратная связь

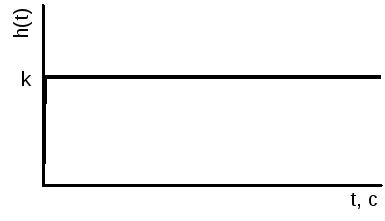
2.3. Уравнения статики элементов

Электронный усилитель
Электромеханический управляющий элемент
Гидравлический усилитель
Гидравлический исполнительный механизм
Обратная связь

2.4. Статические характеристики элементов

Электронный усилитель

Электромеханический управляющий элемент

Гидравлический усилитель

Q_гу,л/с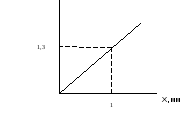

Гидравлический исполнительный механизм

Y, мм

Обратная связь

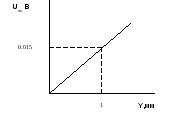
2.5 Передаточные функции элементов САУ

Электронный усилитель (ЭУ):

(6)

Электромеханический управляющий элемент (ЭМУЭ):

- операторное уравнение

-передаточная функция

(7)

Гидравлический усилитель (ГУ):

-операторное уравнение

-передаточная функция

(8)

Гидравлический исполнительный механизм (ГИМ):

-операторное уравнение

-передаточная функция

(9)

Обратная связь (ОС):

(10)

3. Анализ системы управления

3.1. Описание работы системы управления

На первом этапе элемент сравнения сравнивает напряжение выходное (задающее) с напряжением обратной связи. Если имеется разница ΔU сигнал поступает на электронный усилитель, затем усиленный сигнал обрабатывается электронно-механическим управляющим элементом, который воздействует на гидравлический усилитель. Тот в свою очередь управляет гидравлическим исполнительным механизмом, который задает положение штока. Это положение штока исправляет (выравнивает) ошибку отклонения выходного напряжения. В случае отсутствия ΔU, задающее напряжение передается на выход.

3.2. Передаточная функция для выходного сигнала

В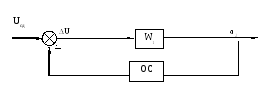 структурной схеме заменяется прямая цепь последовательно соединённых звеньев одним звеном W₁:

W₁=W_эу·W_эмуэ·W_гу·W_гим·W_ос

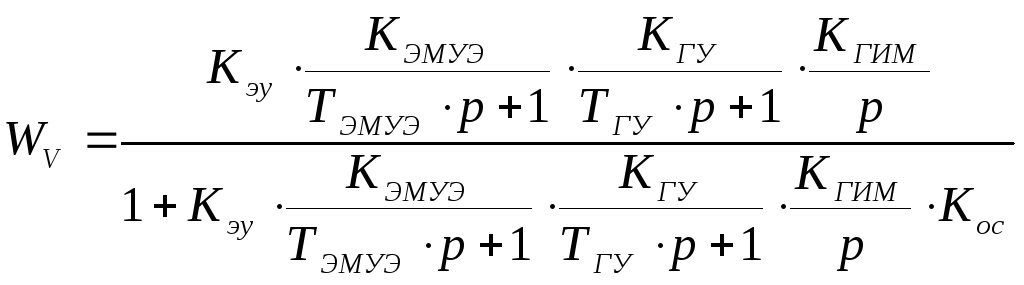
В общем виде:

(12)

Полиномиальные коэффициенты:

(13)

(14)

(15)

(16)

(17)

3.3. Уравнение динамики для выходного сигнала

В соответствие с передаточной функцией получается:

• операторное уравнение:

• дифференциальное уравнение:

(18)

3.4. Уравнение статики и статическая характеристика для выходного сигнала

Уравнение статики:

Статическая характеристика:

4. Выбор параметра системы управления

4.1. Диапазон параметра, в котором система устойчива

Данная система управления описывается уравнением динамики 3-го порядка.

Условие устойчивости Гурвица для системы 3-го порядка:

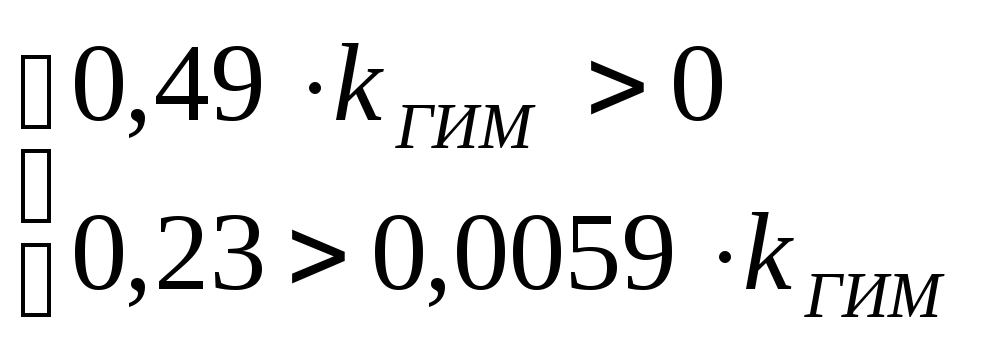
Решая систему неравенств находим диапазон параметра «k_гим», в котором система управления устойчива:

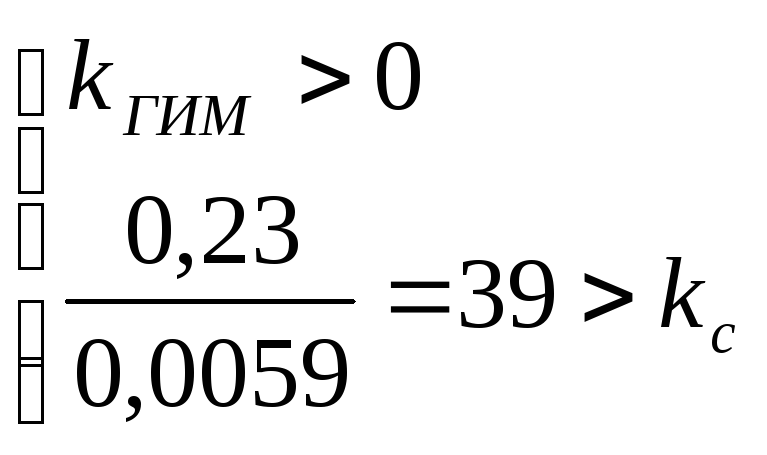
Решая эту систему неравенств с учетом (13) – (17) относительно К_гим получаем диапазон устойчивости САУ:

0< K_гим < 39 мм/л

4.2. Влияние параметра на качество переходного процесса

Интегральная квадратичная оценка для данной системы управления, описываемой передаточной функцией, определяется такой формулой:

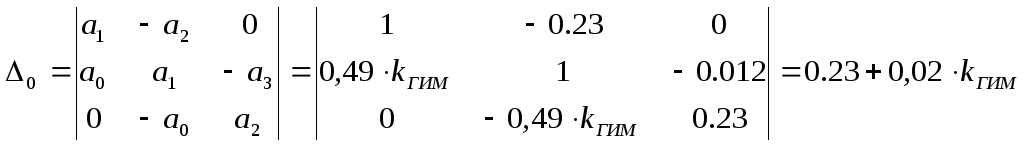
Тогда формула принимает такой вид:

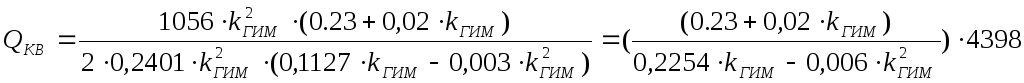
Графически зависимость интегральной квадратичной оценки от параметра «k_гим» в диапазоне устойчивости выглядит так:

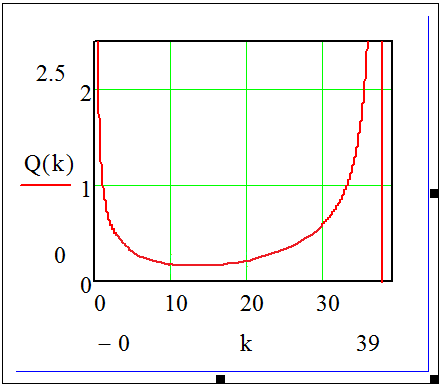
Наилучшее значение «k_гим» будет соответствовать минимальному значению интегральной квадратичной оценки.

Значение параметра для наилучшей работы системы в переходном режиме определяется по графику примерно:

K_гим = 10

6. Моделирование работы системы управления

1. Переходная характеристика системы управления

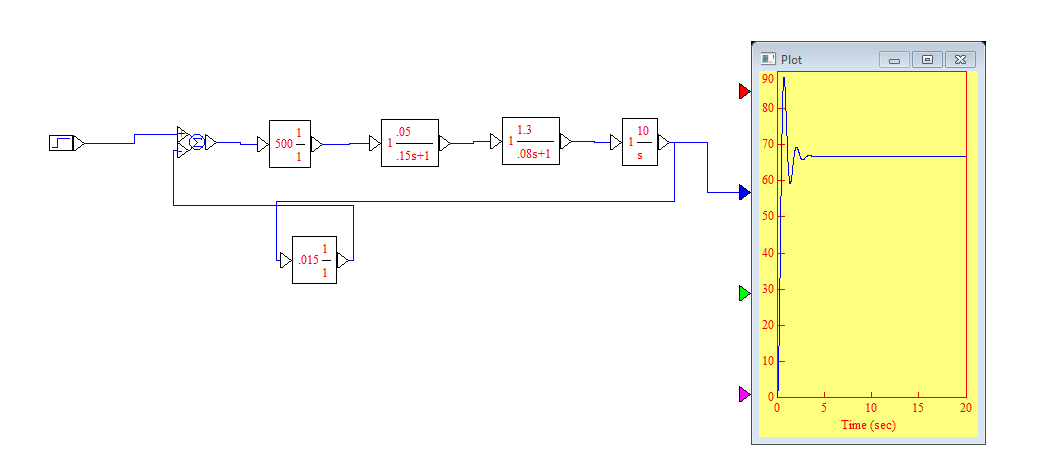
Переходная характеристика получена при оптимальном значении параметра k_гим=10.

Время регулирования системы управления составляет примерно5 с.

Установившееся значение управляемого сигнала на Yуст=66 об/с.

2. Проверка диапазона устойчивости

В блоке ГИМ значение параметра изменяется с оптимального на границу устойчивости 39.

3. Проверка влияния параметра на качество переходного процесса

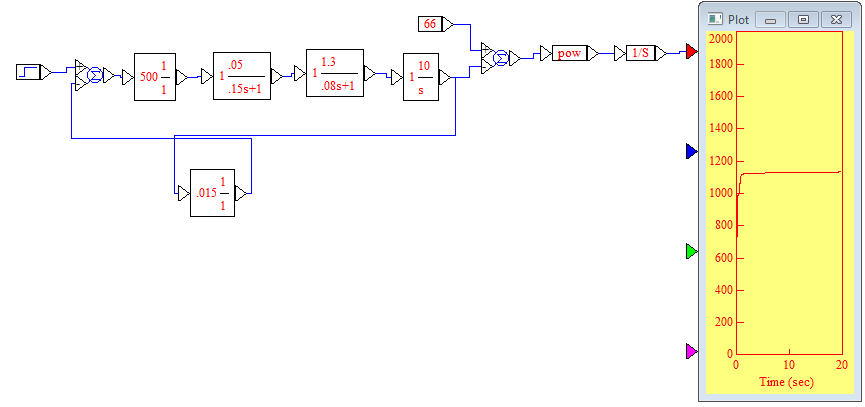
При моделировании подтвердилось, что для оптимального значения параметра k_гим=10 интегральная квадратичная оценка накапливается до величины примерно 1,1*10³

Проверка

В формулу

Подставляем значение k_гим=10

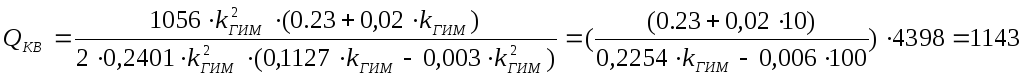
Значение =1143 подтвердилось при моделировании процесса и на графике зависимости квадратичной оценки от параметра « k_гим».