
- •Модуль 7
- •Необходимое условие сходимости ряда
- •Задачи для самостоятельного решения
- •Знакочередующиеся ряды. Признак Лейбница
- •Условная сходимость. Признак Абеля-Дирихле
- •Задачи для самостоятельного решения
- •Занятие 10 Степенные ряды
- •Задачи для самостоятельного решения
- •Задачи для самостоятельного решения
- •Занятия 12 Тригонометрический ряд Фурье функции на интервале
- •Ряд Фурье функции на интервале
- •Задачи для самостоятельного решения
- •Преобразование Фурье
- •Косинус- преобразование и синус-преобразование Фурье
- •Задачи для самостоятельного решения
Модуль 7
«Ряды»
дисциплины
«Математический анализ»
Методическое пособие к практическим занятиям
Методическое пособие к практическим занятиям предназначено для оказания помощи студентам по самостоятельному решению вне аудитории заданий, указанных в семестровом плане (см. документ «План практических занятий»). В нем приводятся подробные решения типовых задач. Особое внимание уделяется наиболее сложным (узловым) этапам решений. После разбора решений типовых заданий настоятельно рекомендуется решить предлагаемые задания для самостоятельного решения.
Занятие 8
Сумма числового ряда. Сходимость
Пример. Исследовать сходимость геометрической прогрессии:
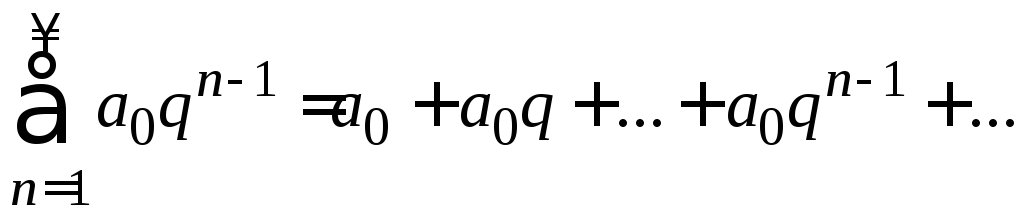 .
.
Решение.
Пусть
![]() обозначает
обозначает![]() -ую
частичную сумму геометрической
прогрессии, т.е.
-ую
частичную сумму геометрической
прогрессии, т.е.![]() .
.
Следовательно,
![]() .
.
Отсюда
![]() и для частичной суммы геометрической
прогрессии справедливо равенство:
и для частичной суммы геометрической
прогрессии справедливо равенство:
 .
.
Находим
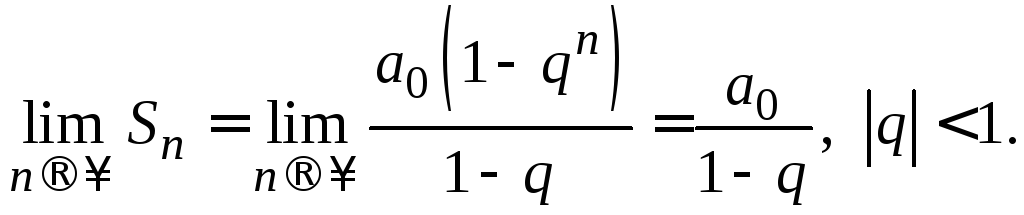
Из
определения сходящегося ряда следует,
что геометрическая прогрессия сходится
тогда и только тогда, когда
![]() и ее сумма, в этом случае, равна
и ее сумма, в этом случае, равна![]() .
.
Ответ:
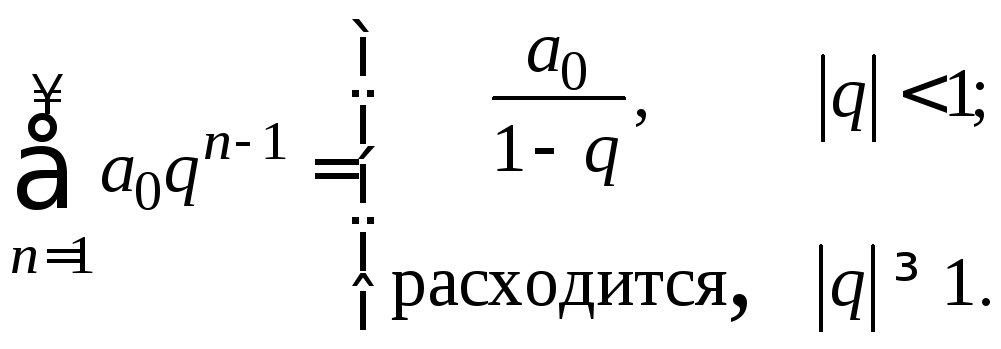
Пример.
Исследовать сходимость ряда
![]() .
.
Решение.
Данный ряд - геометрическая прогрессия,
знаменатель которой
![]() .
.
Следовательно, как следует из примера (2.1.1) ряд сходится.
Ответ:
![]() сходится и его сумма
сходится и его сумма![]() .
.
Необходимое условие сходимости ряда
Пример.
Исследовать сходимость ряда
 .
.
Решение.
Преобразуем модуль
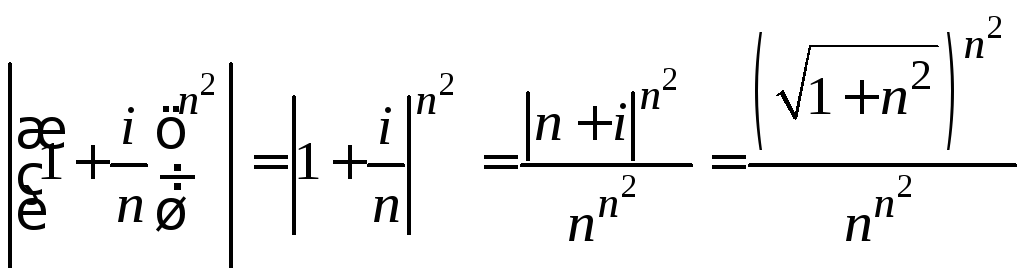 .
Отсюда по второму замечательному пределу
.
Отсюда по второму замечательному пределу
 .
.
Это означает, что не выполнено необходимое условие сходимости и ряд расходится.
Ответ:
ряд
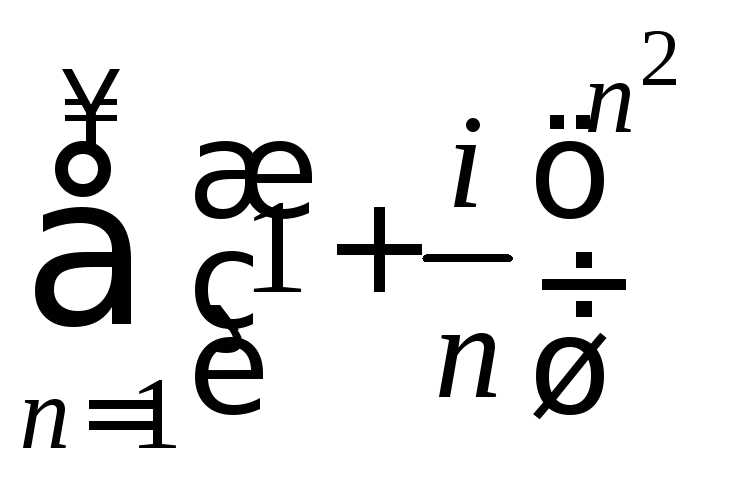 расходится.
расходится.
Признаки сравнения рядов
Пример.
Исследовать сходимость ряда
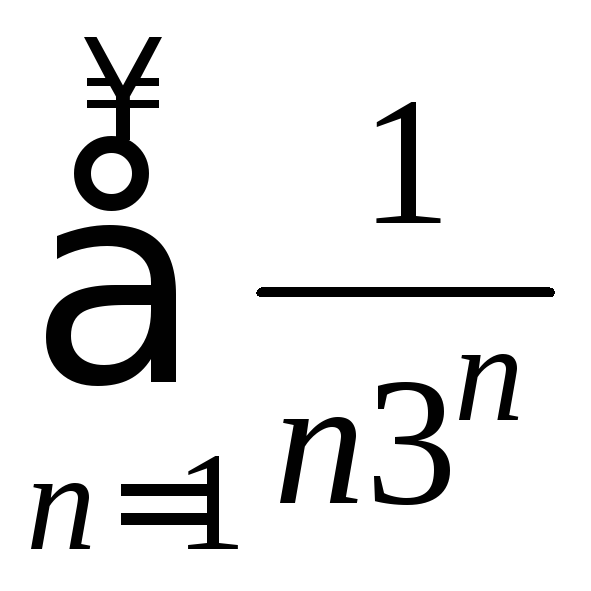 .
.
Решение.
Как показано в примере (2.1.2) ряд
![]() сходится.
Кроме того, имеет место неравенство
сходится.
Кроме того, имеет место неравенство![]() при всех
при всех![]() .
Так как члены исследуемого ряда меньше
членов сходящегося ряда, то данный ряд
также сходится.
.
Так как члены исследуемого ряда меньше
членов сходящегося ряда, то данный ряд
также сходится.
Ответ:
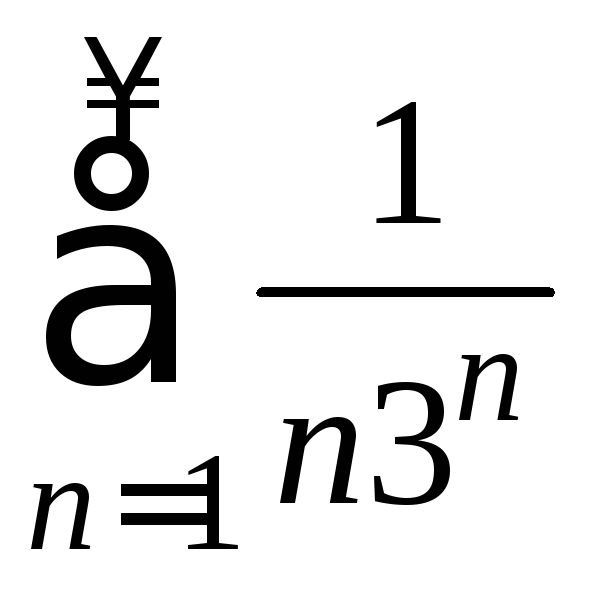 сходится.
сходится.
Предельный признак сравнения
Пусть
![]() ,
,![]() и
и![]() ,
,![]() .
Тогда ряды
.
Тогда ряды![]() и
и![]() сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
Пример.
Исследовать сходимость ряда
 .
.
Решение.
Как известно, гармонический ряд
![]() расходится. Поэтому по предельному
признаку сравнения расходится ряд
расходится. Поэтому по предельному
признаку сравнения расходится ряд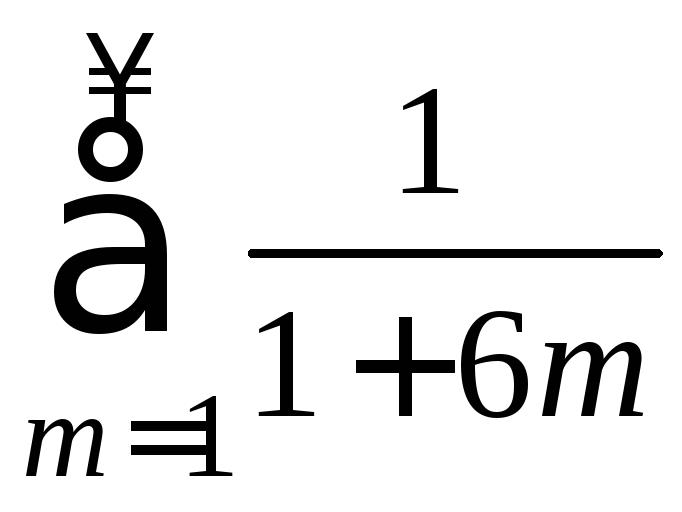 ,
так как
,
так как
![]() .
.
Ответ:
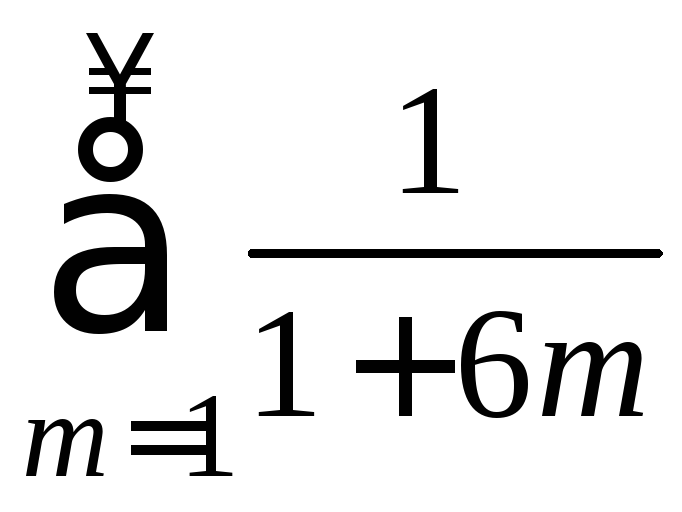 расходится.
расходится.
Задачи для самостоятельного решения
В задачах 1 – 15 исследовать сходимость числового ряда с общим членом un.
1.
![]() .2.
.2.
![]() .
.
3.
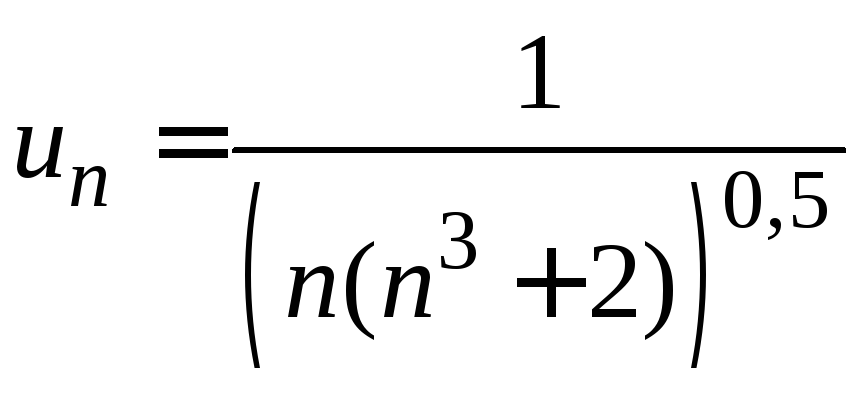 .4.
.4.
![]() .
.
5.
![]() .6.
.6.
![]() .
.
7.
![]() .8.
.8.
![]() .
.
9.
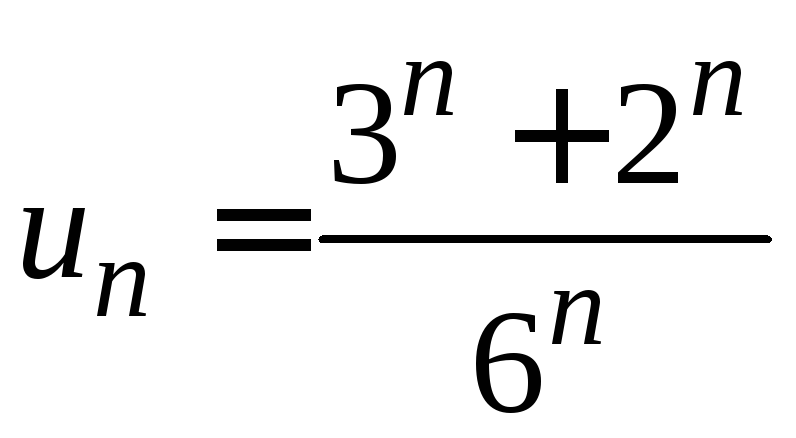 .10.
.10.
![]() .
.
11.
![]() .12.
.12.
![]() .
.
13.
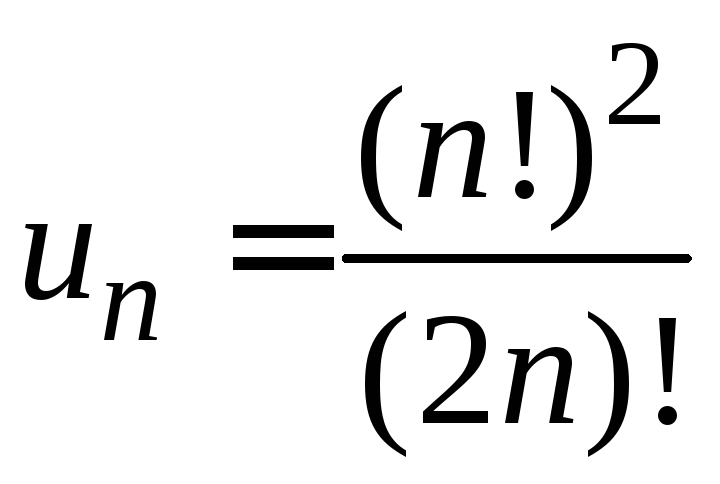 .14.
.14.
![]() .
.
15.
![]() .
.
Ответы.
1. Расходится. 2. Сходится. 3. Сходится. 4. Сходится. 5. Сходится. 6. Сходится при а > 1. 7. Сходится. 8. Сходится. 9. Сходится. 10. Сходится. 11. Расходится. 12. Сходится. 13. Сходится. 14. Сходится при α > 0. 15. Расходится.
Занятие 9
Признак Даламбера
Пример.
Исследовать сходимость ряда
 .
.
Решение. Исследуем сходимость по признаку Даламбера, а именно, найдем
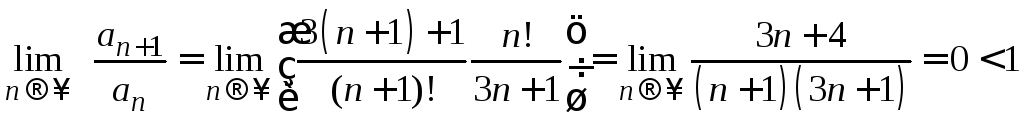 .
.
Следовательно, по признаку Даламбера ряд сходится.
Ответ:
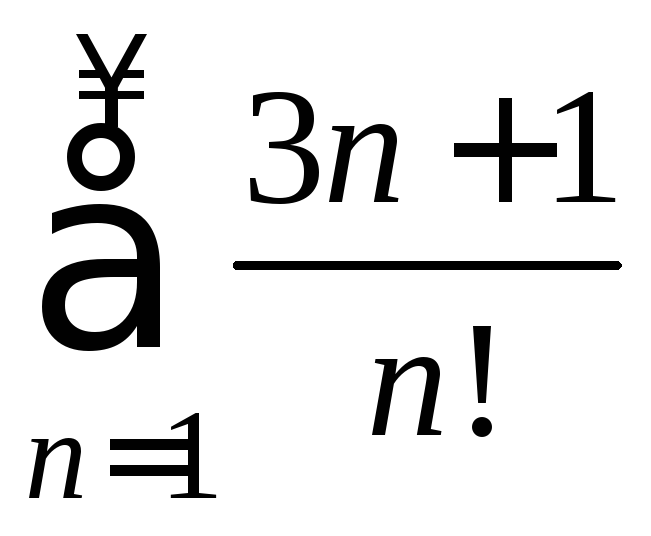 сходится.
сходится.
Признак Коши
Пример.
Исследовать сходимость ряда
 .
.
Решение. Для применения признака Коши преобразуем модуль
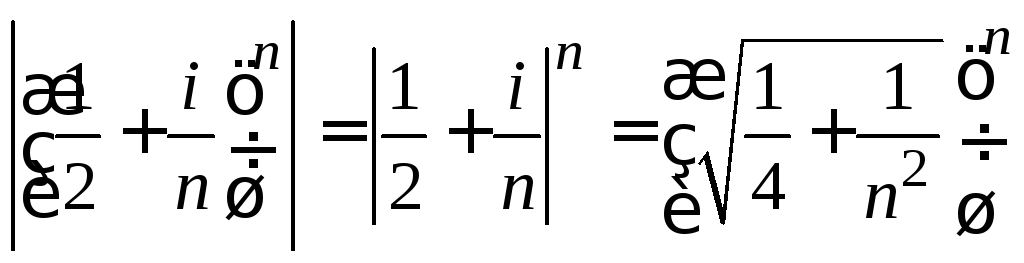 .
.
Отсюда
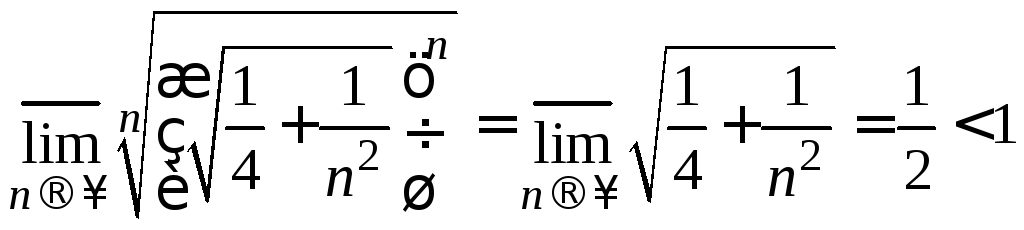 .
.
Поэтому по признаку Коши ряд сходится абсолютно.
Ответ:
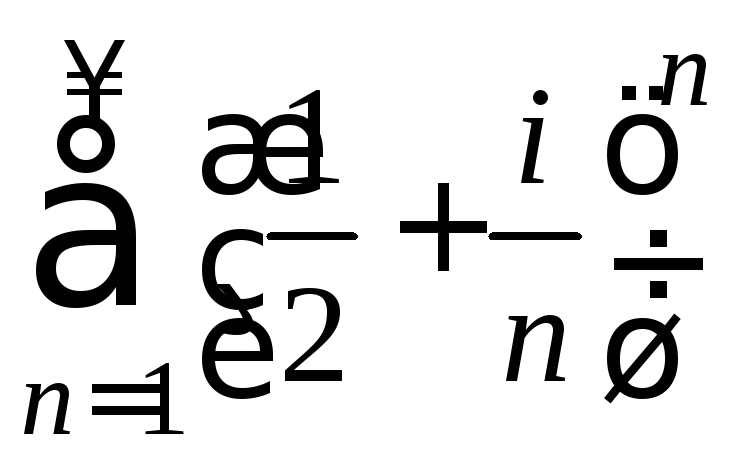 сходится
абсолютно.
сходится
абсолютно.
Интегральный признак Коши
Пример. Исследовать по интегральному признаку сходимость ряда Дирихле.
Решение.
Рядом Дирихле называется ряд вида
![]() .
Так как
.
Так как![]() при всех
при всех![]() и
и![]() ,
то исследуем сходимость по интегральному
признаку сходимости. Вычисляем
,
то исследуем сходимость по интегральному
признаку сходимости. Вычисляем
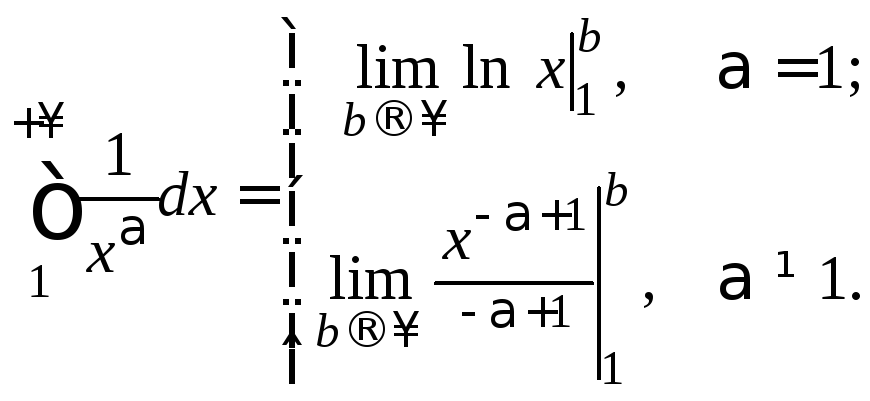
Отсюда
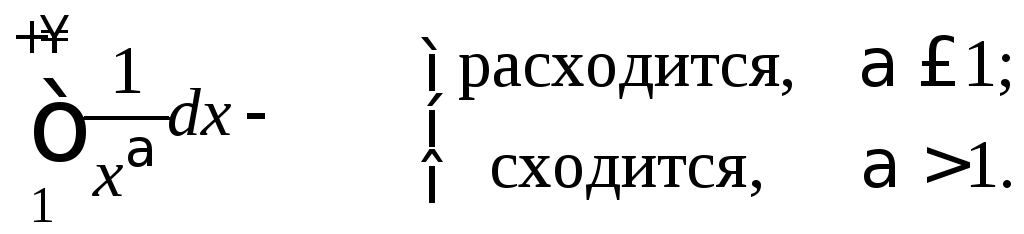
Соответственно,
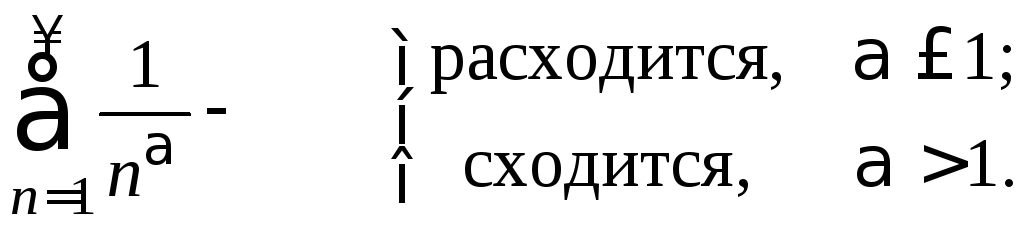
Ответ:
ряд
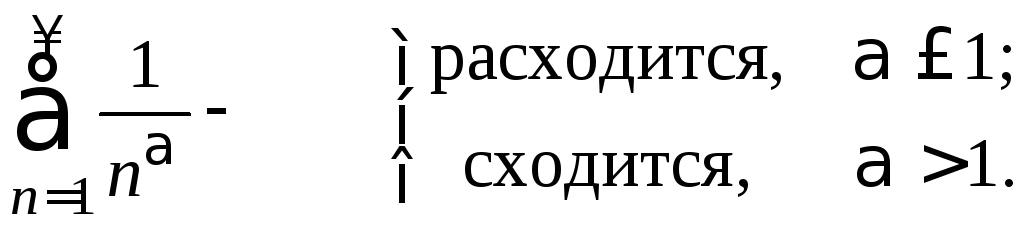
Ряд
Дирихле
![]() сходится, если
сходится, если![]() и расходится, если
и расходится, если![]() .
.
Пример.
Исследовать сходимость гармонического
ряда
![]() .
.
Решение.
Гармонический ряд
![]() – это частный случай ряда Дирихле
– это частный случай ряда Дирихле![]() с
с![]() .
Поэтому ряд расходится.
.
Поэтому ряд расходится.
Ответ:
![]() расходится.
расходится.
Пример.
Исследовать сходимость ряда
![]() .
.
Решение.
Ряд
![]() – это частный случай ряда Дирихле
– это частный случай ряда Дирихле![]() с
с![]() .
Поэтому ряд сходится.
.
Поэтому ряд сходится.
Ответ:
![]() сходится.
сходится.
