3 семестр ЭКТ / Аннотации с дисциплине / mppz_M8_vm2_x_MatAn_x

Модуль 8

«Уравнения в частных производных»

дисциплины

«Математический анализ»

Методическое пособие к практическим занятиям

Методическое пособие к практическим занятиям предназначено для оказания помощи студентам по самостоятельному решению вне аудитории заданий, указанных в семестровом плане (см. документ «План практических занятий»). В нем приводятся подробные решения типовых задач. Особое внимание уделяется наиболее сложным (узловым) этапам решений. После разбора решений типовых заданий настоятельно рекомендуется решить предлагаемые задания для самостоятельного решения.

Метод Фурье разделения переменных для уравнений в частных производных Пример. Найти распределение температуры в стержне для рассмотренной выше задачи, если

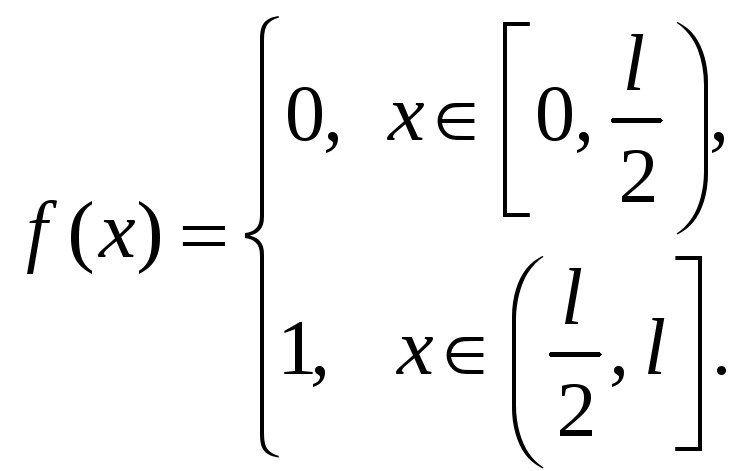
Решение. Чтобы получить ответ, необходимо лишь вычислить интегралы:

.

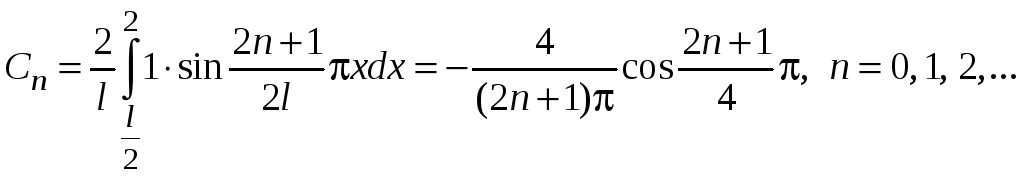Р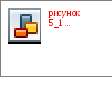 ешение задачи с данным начальным распределением температуры имеет вид

Графики распределения температуры в различные моменты времени показаны на рисунке.

С физической точки зрения через достаточно большое время все тепло, которое первоначально было в стержне, уйдет через левый торец, и температура всех точек станет равной нулю. Это же видно и из решения: с ростом экспоненты в каждом слагаемом ряда стремятся к нулю, и, следовательно, для всех .

Пример. Решить уравнение , , если и .

Решение. Ищем решение в виде , где функция определяется из уравнения следующим образом:

.

Из граничных условий получаем, что и, таким образом, , а для функции имеем задачу , , и .

Как и выше, общее решение записываем в виде

,

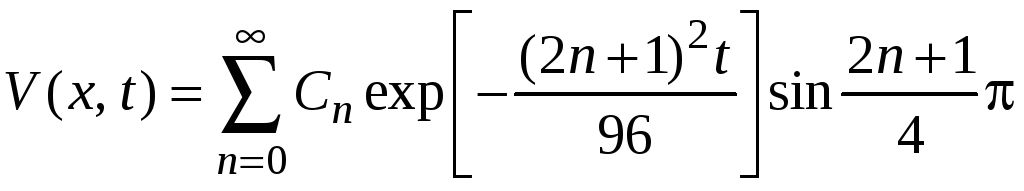где коэффициенты определяются по формулам

,

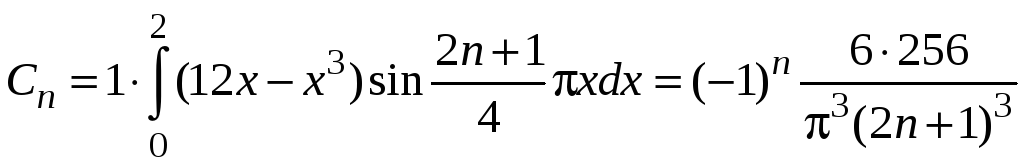после чего мы получаем ответ для задачи данного примера

.

Отметим особенность этого решения: при ряд стремится к тождественному нулю. Это отражает тот факт, что переходные процессы с ростом затухают и в решении остается только слагаемое , которое описывает установившееся распределение температур в стержне, связанное с постоянно действующими в стержне источниками тепла .

Пусть теперь в неоднородном уравнении функция зависит от обеих переменных

. (1)

Граничные условия возьмем такими же, как и в предыдущей задаче

, (2)

а начальное условие нулевым

. (3)

Сначала находим собственные функции однородного уравнения из граничных условий (2). Они уже были получены ранее, это . Решение задачи (1-3) будем искать в виде ряда

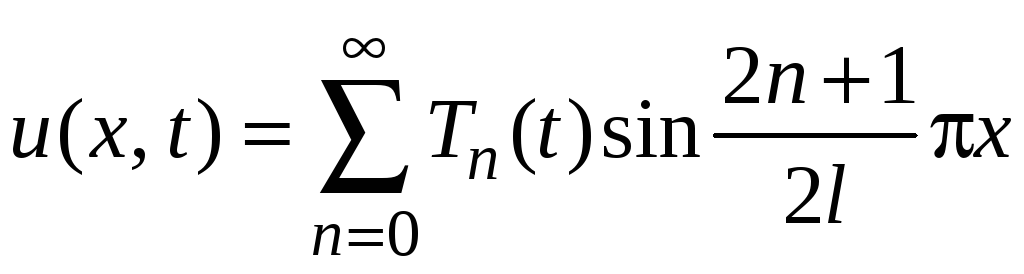, (4)

где – неизвестные функции. Подстановка этого ряда в начальное условие (3) дает

,

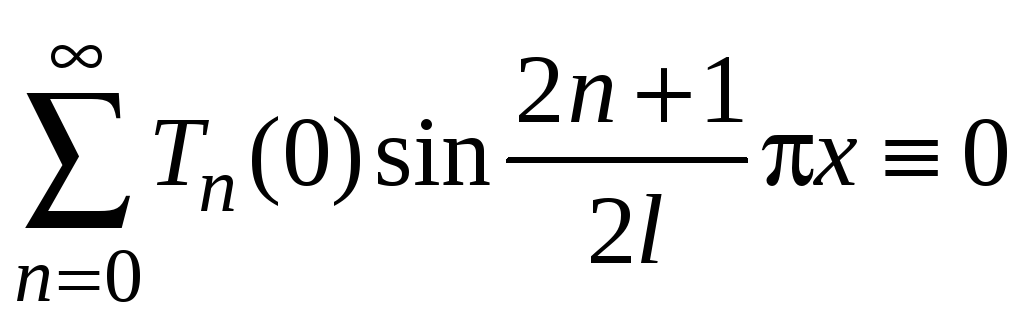откуда сразу получаем, что

для всех .

Теперь подставляем ряд (4) в уравнение (1):

.

Разложив функцию в ряд по собственным функциям , приходим к равенству

,

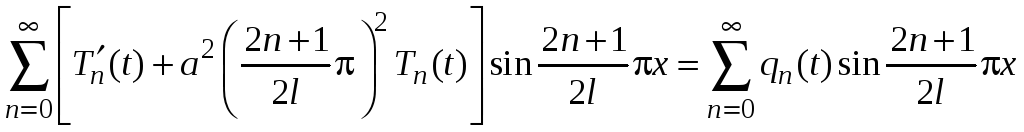где

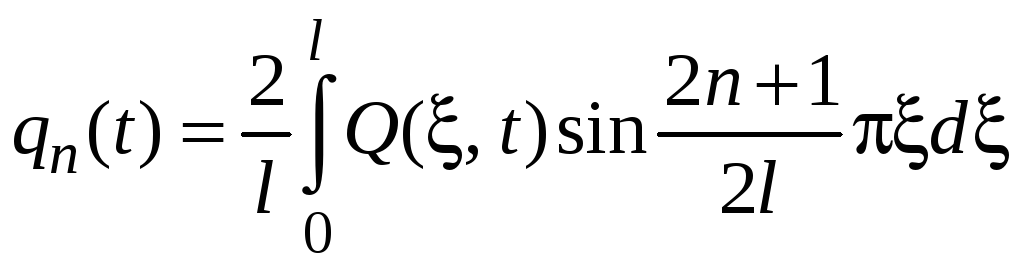. (5)

Из равенства двух рядов следует, что для всех

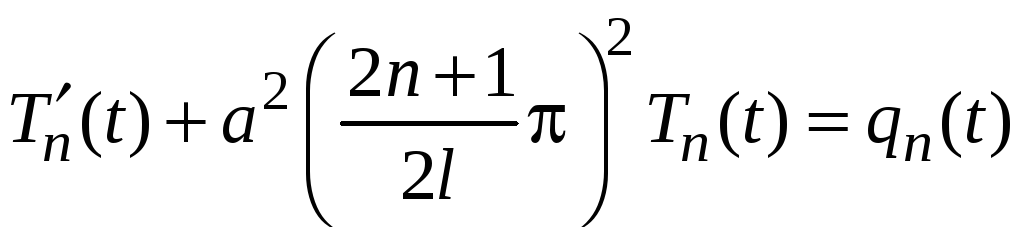. (6)

С учетом начальных условий

получаем задачу Коши, из которой все определяются однозначно.

Пример. Решить уравнение , если , и .

Решение. Поскольку собственные функции однородной задачи уже найдены выше, необходимо найти функции .

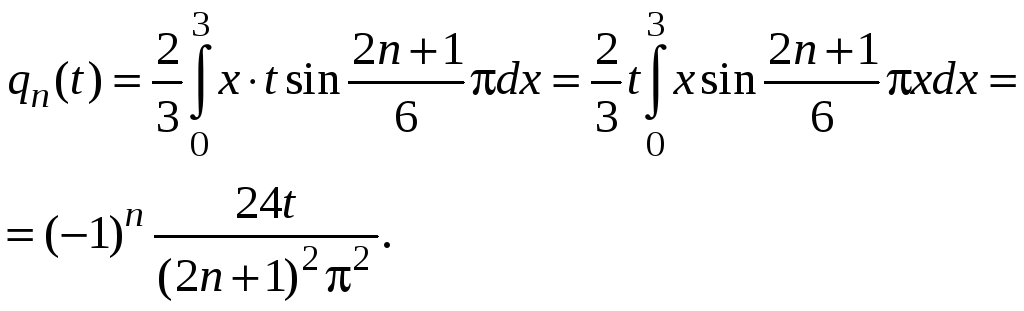
Для отыскания имеем задачу Коши

,

где введены обозначения и .

Решение этой задачи Коши таково:

.

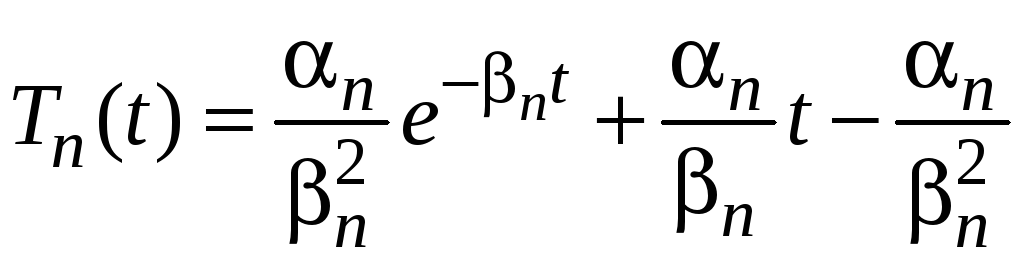Подставляя эти функции в ряд (4) и заменяя и их значениями, получаем ответ

5