
2 семестр ЭКТ / Всё подряд / Exam_EKT-1_12-13_MatAn_2sem_1
.doc-
Программа экзамена по курсу "Математический анализ", ЭКТ-1
2-й семестр 2012/2013 уч. год
Неопределенный интеграл.
1. Первообразная, ее свойства. Неопределенный интеграл.
2. Таблица неопределенных интегралов.
3. Замена переменной и интегрирования по частям в неопределенном интеграле.
4. Интегрирование рациональных дробей, иррациональностей, тригонометрических выражений (уметь вычислять интегралы).
Определенный интеграл.
1. Задача о площади. Определение определенного интеграла и его геометрический смысл.
2. Необходимое условие интегрируемости. Пример ограниченной неинтегрируемой функции.
3. Свойства определенного интеграла (линейность, аддитивность, сохранение неравенства).
4. Свойства интеграла с переменным верхним пределом. Существование первообразной для непрерывной функции.
5. Формула Ньютона-Лейбница.
6. Замена переменной и интегрирование по частям в определенном интеграле.
7. Теорема о среднем для определенного интеграла.
8. Понятие несобственного интеграла с единственной особенностью. Примеры.
9. Критерий Коши сходимости несобственных интегралов.
10. Несобственные интегралы от неотрицательных функций. Признаки сравнения.
11. Абсолютная и условная сходимость несобственных интегралов. Примеры.
12. Вычисление площадей плоских фигур в декартовых и полярных координатах.
13. Длина дуги кривой.
14. Объем тела вращения.
15. Площадь поверхности тела вращения.
Функции многих переменных.
-
Пространство Rn. Понятие сходимости последовательности в Rn. Связь сходимости в Rn с покоординатной сходимостью. Свойства сходящихся последовательностей. Фундаментальные последовательности. Полнота Rn .
-
Понятия окрестности точки, открытого, связного множества и области в Rn.
-
Предел и непрерывность функции многих переменных. Определения. Свойства (арифметические, сохранение знака). Непрерывность сложной функции.
-
Частные производные. Теорема о смешанных производных (без док-ва).
-
Понятие дифференцируемости функций многих переменных. Дифференциал. Необходимое условия дифференцируемости. Достаточное условие дифференцируемости.
-
Применение первого дифференциала в приближенных вычислениях.
-
Дифференцирование сложной функции. Производная неявной функции.
-
Касательная плоскость и нормаль к поверхности заданной явным или неявным уравнением.
-
Градиент и производная по направлению. Геометрический и физический смысл градиента.
-
Дифференциалы высших порядков функции многих переменных.
-
Формула Тейлора для функции многих переменных.
-
Экстремум функции многих переменных. Необходимые условия. Стационарные точки. Достаточные условия (представление приращения функции в стационарной точке через дифференциал 2-го порядка и достаточные условия на языке квадратичных форм и через угловые миноры матрицы Гессе).
Кратные интегралы.
1. Определение двойного и тройного интегралов: для случая прямоугольной области, для произвольной области. Геометрический и физический смысл двойного и тройного интегралов.
2. Вычисление кратных интегралов путем перехода к повторному интегралу: для случая прямоугольной области, для произвольной области.
3. Полярная, цилиндрическая и сферическая система координат и их якобианы.
4. Понятие якобиана и формулу замены переменных в кратных интегралах. Обоснование формулы для полярной системы координат.
5. Понятие площади поверхности, заданной явным уравнением. Формула для вычисления площади. Обоснование формулы.
Программа базового уровня по курсу
«Математический анализ», ЭКТ - I, 2 семестр, 2012-13 уч. год.
1. Неопределенный интеграл
Знать
-
определение первообразной
-
определение неопределенного интеграла
-
свойства первообразной
-
таблицу неопределенных интегралов
-
формулу интегрирования по частям
-
формулу замены переменной
Уметь
-
Находить первообразные для функций
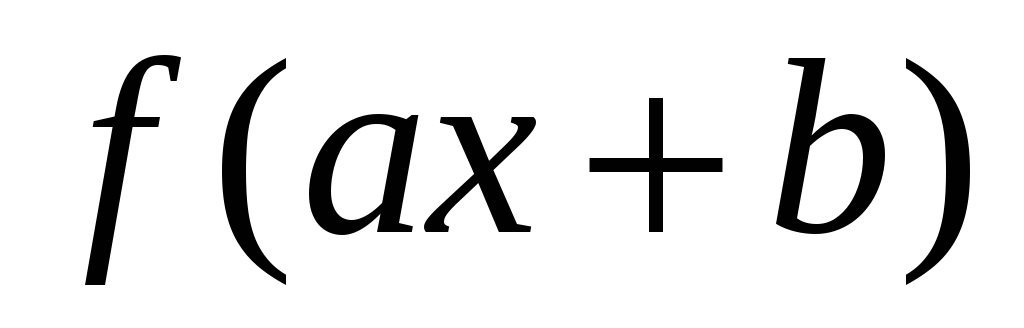 ,
если
,
если
 является табличным
является табличным -
Находить неопределенные интегралы от функций, равных сумме (разности) «табличных»
-
Вычислять с помощью подведения под знак дифференциала неопределенные интегралы вида
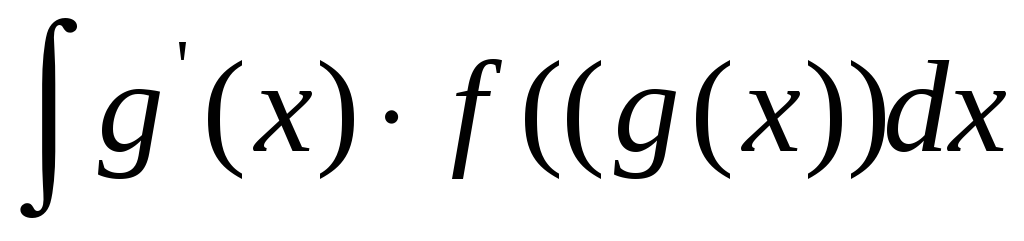 ,
где
,
где
 - табличный,
- табличный,
 - основная элементарная функция
(например,
- основная элементарная функция
(например,
 ).
). -
Уметь интегрировать по частям интегралы типа
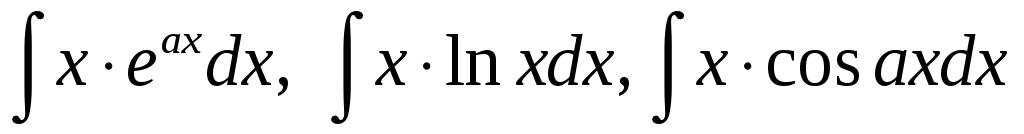 .
. -
Уметь интегрировать дроби вида
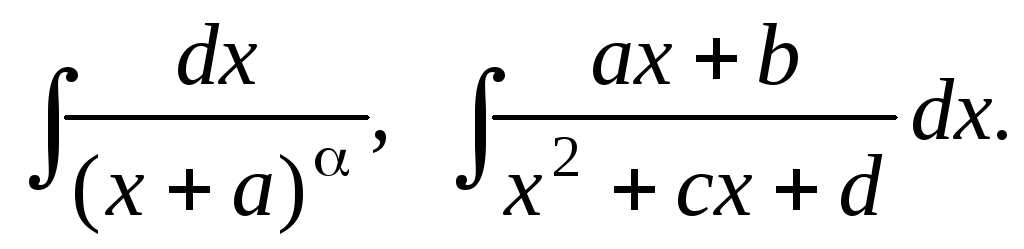
2. Определенный интеграл
Знать
-
понятие разбиения
-
понятие интегральной суммы
-
понятие мелкости (диаметра) разбиения
-
определение определенного интеграла
-
формулу Ньютона-Лейбница
-
формулу интегрирования по частям
-
формулу замены переменной
Уметь
-
Вычислять с помощью формулы Ньютона-Лейбница определенные интегралы аналогичные пунктам 1.7-1.11
3. Несобственный интеграл
Знать
-
определения несобственных интегралов от неограниченных функций и на неограниченном промежутке
-
понятие абсолютно сходящегося интеграла
-
признаки сравнения сходимости несобственных интегралов
-
условия сходимости несобственных интегралов вида

Уметь
-
Распознавать несобственные интегралы
-
Вычислять по определению несобственные интегралы вида
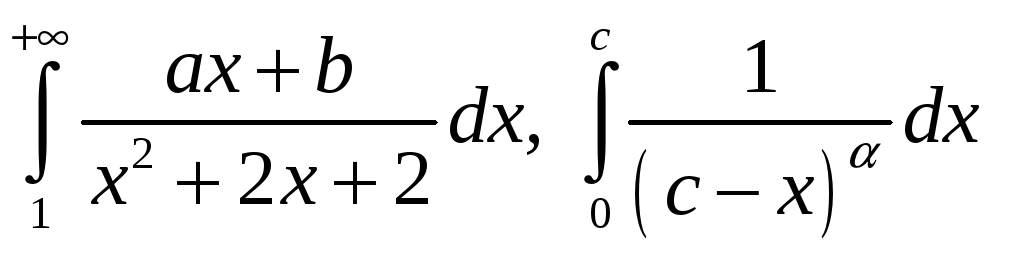
-
Применять признаки сравнения для исследования сходимости интегралов вида
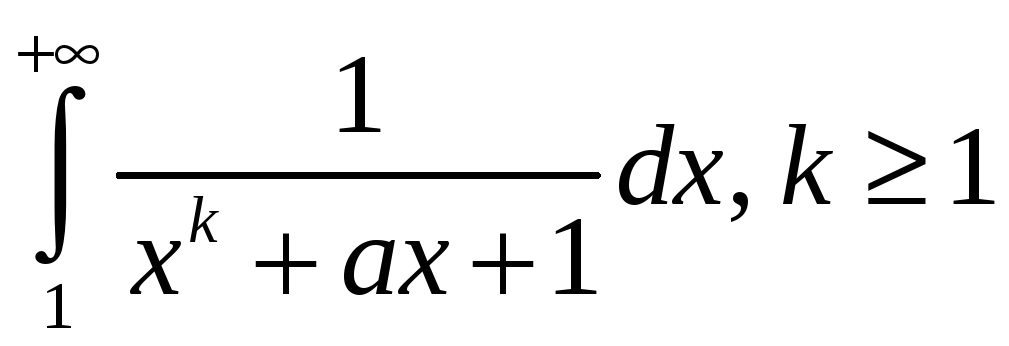 .
.
4. Приложения определенного интеграла
Знать
-
формулу для вычисления площади криволинейной трапеции в декартовых и полярных координатах
-
формулу для вычисления объема тела вращения
-
формулы для вычисления длины дуги плоской кривой заданной параметрически или в явном виде
-
формулу для вычисления площади поверхности вращения
Уметь
-
Вычислять площадь фигуры, ограниченной двумя параболами или параболой и прямой.
-
Вычислять объем тела, образованного вращением криволинейной трапеции
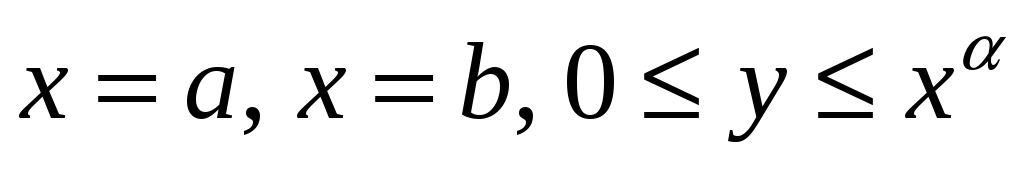 вокруг оси
вокруг оси
 .
. -
Вычислять площадь поверхности, образованной вращением кривой
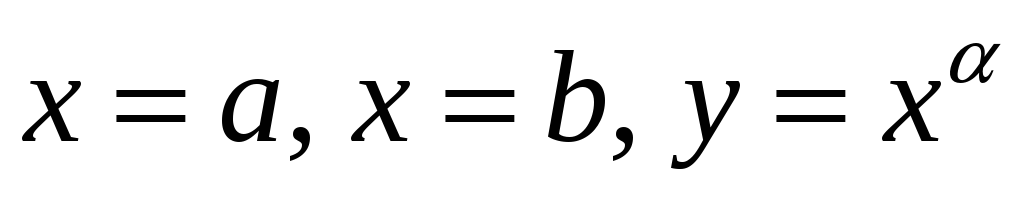 вокруг оси
вокруг оси
 .
. -
Вычислять длину дуги кривой типа
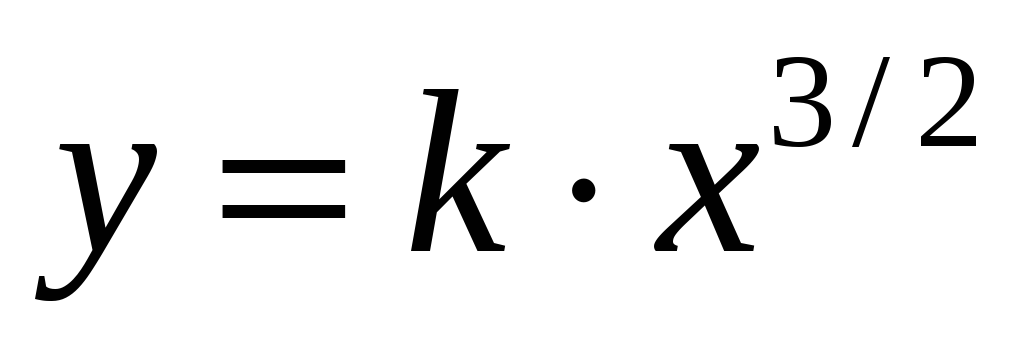 ,
,
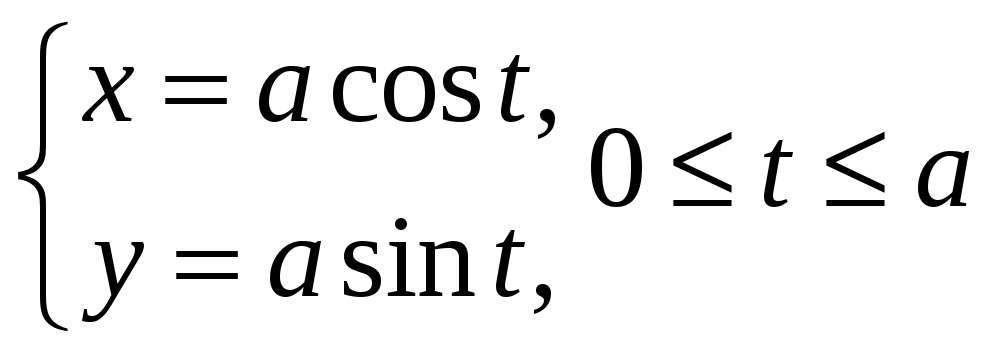 ,
,
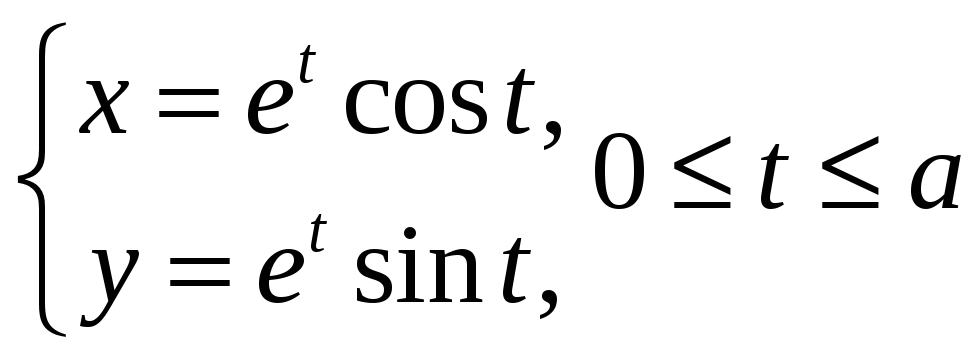
5. Функции многих переменных
Знать
-
определение частной производной
-
определение дифференцируемости функции двух переменных
-
определение дифференциала
-
определение производной по направлению и формулу для её вычисления
-
определение градиента
-
формы для дифференциалов 1-го и 2-го порядков функций 2-х и 3-х переменных
-
уравнения касательной плоскости и нормали к поверхности
-
определение локального экстремума
-
необходимые условия экстремума
-
достаточные условия экстремума (для функций 2-х и 3-х переменных)
Уметь
-
находить область определения функции двух переменных и изображать её на плоскости (область определения может ограничиваться окружностями, параболами, прямыми, гиперболами)
-
Находить частные производные первого и второго порядков
-
Записывать дифференциал первого и второго порядков для функции 2-х и 3-х переменных
-
находить градиент, модуль градиента
-
находить производную по направлению
-
записывать уравнения касательной плоскости и нормали для поверхности, заданной уравнением
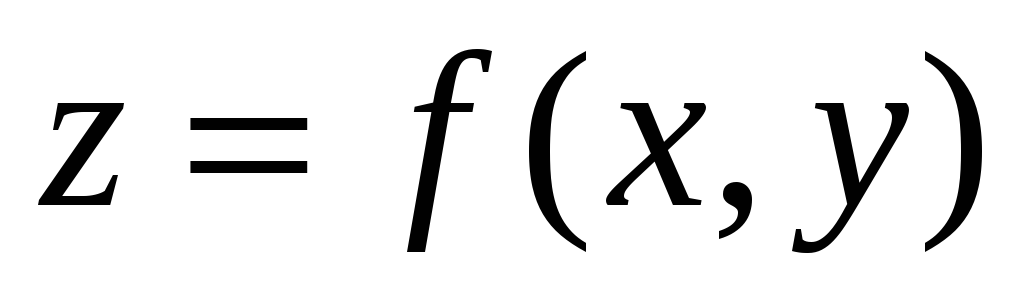
-
Исследовать на экстремум функции вида
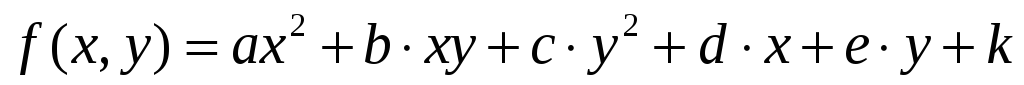 ,
,
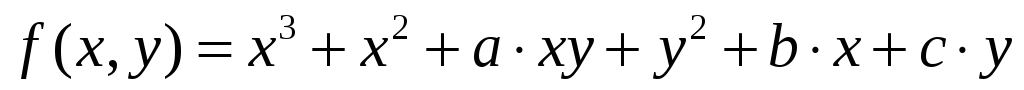
Кратные интегралы
Знать
6.1. определение двойного интеграла для прямоугольной области и для произвольной области
6.2. формулы, связывающие декартовые координаты точки с полярными, цилиндрическими, сферическими координатами точки
6.3. формулы замены переменной в кратных интегралах для случаев полярной, цилиндрической, сферической систем координат
6.4. формулу для вычисления площади поверхности
Уметь
6.5. Вычислять двойные интегралы для прямоугольной области.
6.6. Расставлять пределы интегрирования в повторном интеграле для несложных плоских областей.
6.7. Вычислять несложные двойные интегралы с помощью переходя к полярной системе координат
Примечание.
Для получения оценки 4 необходимо уметь доказывать указанные в программе базового уровня свойства, условия и формулы (кроме достаточных условий экстремума и длины дуги, заданной параметрически).
ОБРАЗЕЦ ВАРИАНТА (ЭКТ-1, 2 семестр, 2012-13 учебный год)
-
Дать определение мелкости (диаметра) разбиения
-
Сформулировать определение интегральной суммы.
-
Дать определение определенного интеграла.
-
Дать определение локального экстремума (для функции двух переменных) (или дать определение двойного интеграла)
-
Доказать необходимые условия экстремума (для функций двух переменных) (или записать и обосновать формулу перехода к полярным координатам в двойном интеграле).
-
Сформулировать достаточные условия экстремума (для функций двух переменных).
Вычислить:
-
 . 8.
. 8.
 . 9.
. 9.
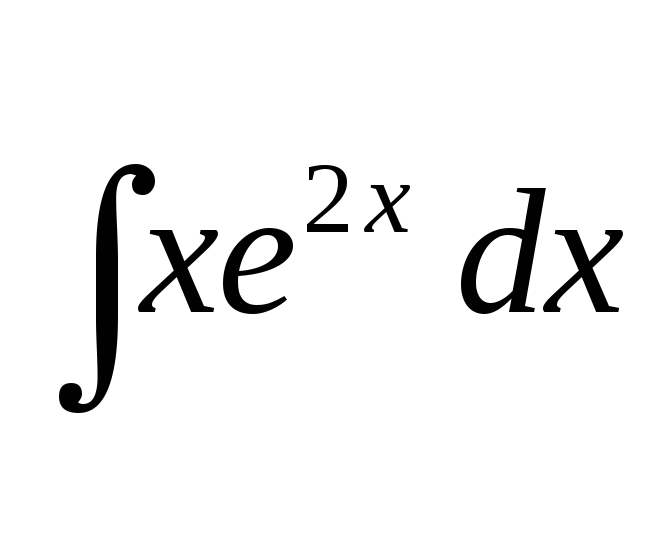 .
.
10.
![]() (или
(или
![]() ,
где область
,
где область
![]() ограничена линиями
ограничена линиями
![]() ).
).
-
Найти длину дуги кривой
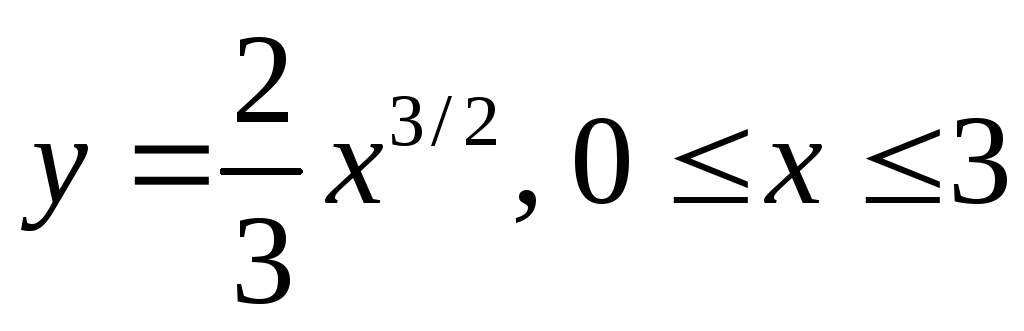 .
.
12.
Изобразить область определения функции
![]() .
.
13. Найти
![]() для функции
для функции
![]() .
.
1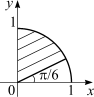 4.
Найти модуль (длину) градиента функции
4.
Найти модуль (длину) градиента функции
![]() в точке (1, -1) (или
вычислите
с помощью замены переменных
в точке (1, -1) (или
вычислите
с помощью замены переменных
![]() ,
где область
,
где область
![]() задана на рисунке).
задана на рисунке).
-
Найти точки экстремума функции
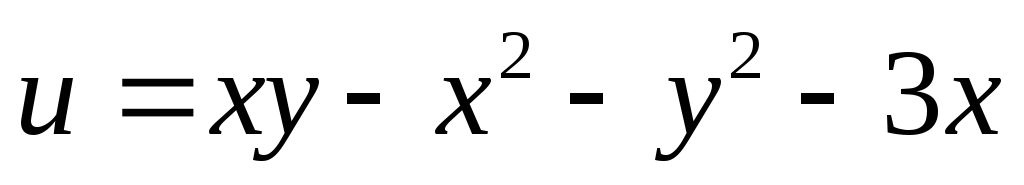 .
.
Критерии оценок (за ответ на экзамене):
20 баллов – зачтено не менее 10 заданий.
30 баллов – зачтено не менее 13 заданий, причем зачтено хотя бы одно из заданий, в котором нужно было дать доказательство утверждения или сделать вывод формулы.
Для получения 40 баллов на экзамене необходимо получить 30 баллов по варианту и пройти собеседование с лектором
Окончательная оценка в ведомость и зачетную книжку ставится на основании набранной суммы баллов в семестре и баллов за ответ на экзамене
