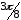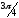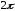ИПР_2.вариант 5
.docxМинистерство образования Республики Беларусь
Учреждение образования «Белорусский государственный университет информатики и радиоэлектроники»
Факультет непрерывного и дистанционного обучения
Кафедра высшей математики
МАТЕМАТИКА, ЧАСТЬ 1
ИНДИВИДУАЛЬНАЯ ПРАКТИЧЕСКАЯ РАБОТА №1-2
«ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ»
Минск 2016
Задача 1
Укажите, является ли данная числовая последовательность бесконечно малой (б.м.ч.п.), бесконечно большой (б.б.ч.п.), ограниченной числовой последовательностью.
1.5. 
Решение
Можно найти несколько пределов данной числовой последовательности. Для этого нужно посмотреть, что произойдет с ней при стремлении к бесконечности с разными знаками

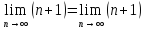



А)![]() →+∞
предел равен ∞
→+∞
предел равен ∞
Б)![]() →+∞
предел равен ∞
→+∞
предел равен ∞
Мы
видим, что при стремлении к бесконечности,
мы имеем бесконечность, следовательно,
данная
числовая последовательность является
бесконечно большой, т.к.
для любого А>0
существует номе
![]() такой,
что для любого
такой,
что для любого
![]() выполняется неравенство
выполняется неравенство
![]() .
.
Задача 2
Найдите предел числовой последовательности. Укажите, является ли данная числовая последовательность бесконечно малой (б.м.ч.п.), бесконечно большой (б.б.ч.п.), ограниченной числовой последовательностью.
2.5. 
Решение
Можно найти несколько пределов данной числовой последовательности. Для этого нужно посмотреть, что произойдет с ней при стремлении к бесконечности с разными знаками, и в "опасных" точках.
"Опасные" точки сразу видны, это:
1) ![]() -
знаменатель обращается в 0.
-
знаменатель обращается в 0.
2) ![]() -
по обычаю проверяется эта точка.
-
по обычаю проверяется эта точка.
Используя
свойства второго замечательного
предела:
![]() Получаем:
Получаем:

здесь a = 1, b = 3/7
Посчитаем,
что получилось: (при ![]() →∞)
→∞)
Итак:
1) ![]() →+∞
предел равен
→+∞
предел равен ![]()
2) ![]() →-∞
предел равен
→-∞
предел равен ![]()
3) ![]() →0
предел равен:
→0
предел равен:

4) ![]() →
→![]()
Мы видим, что при стремлении к бесконечности с разными знаками, мы имеем конечное число. В "опасных" точках, скачков нет.
Используя
свойства показательной функции, находим,
что график делает скачок в некотором
интервале (основание должно быть
неотрицательным числом, если же взять
число из интервала ![]() -
мы получаем отрицательное основание).
-
мы получаем отрицательное основание).
Можно
говорить, что данная числовая
последовательность является бесконечно
большой
, т.к.
для любого А>0 существует номе
![]() такой,
что для любого
такой,
что для любого
![]() выполняется неравенство
выполняется неравенство
![]() .
.
Задача 3
Выделите в заданной функции полный квадрат и постройте её график в декартовой системе координат путём преобразования графика функции у=х2.
3.5. ![]()
Решение
Выделив полный квадрат в заданной функции, получим

Теперь
применим метод преобразования координат.
Известно, что график функции
![]() получают путем переноса графика
получают путем переноса графика
![]() вверх или вниз вдоль оси OY
на
вверх или вниз вдоль оси OY
на
![]() в зависимости от знака b,
график функции
в зависимости от знака b,
график функции
![]() получается параллельным переносом
графика
получается параллельным переносом
графика
![]() при
при
![]() в положительном направлении оси ОХ
на с,
и в отрицательном направлении этой оси
при
в положительном направлении оси ОХ
на с,
и в отрицательном направлении этой оси
при
![]() ,
а график функции
,
а график функции
![]() получается растяжением графика
получается растяжением графика
![]() вдоль оси ОY
в А
раз при
вдоль оси ОY
в А
раз при
![]() или сжатием вдоль этой оси в А
раз при
или сжатием вдоль этой оси в А
раз при
![]() .
График функции y
= - f(x)
симметрично отобразится относительно
оси OX.
.
График функции y
= - f(x)
симметрично отобразится относительно
оси OX.
 -
парабола с вершиной в точке (1;7).
-
парабола с вершиной в точке (1;7).

 -
сдвиг вправо на 1 ед. параболы
-
сдвиг вправо на 1 ед. параболы
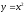
 -
растяжение в 2 раза вдоль оси OY
параболы
-
растяжение в 2 раза вдоль оси OY
параболы

 -
симметричное
отображение относительно оси OX
параболы
-
симметричное
отображение относительно оси OX
параболы

 -
сдвиг вверх на 7ед. параболы
-
сдвиг вверх на 7ед. параболы

Y
7


1
X
Задача 4
Постройте
график функции r=r(φ),
заданной в полярных координатах, для ![]() по
точкам с шагом π/8, если полюс совпадает
с началом декартовой системы координат,
а полярная ось – с осью ОХ.
Найдите каноническое уравнение полученной
линии в декартовой системе координат
и определите её тип.
по
точкам с шагом π/8, если полюс совпадает
с началом декартовой системы координат,
а полярная ось – с осью ОХ.
Найдите каноническое уравнение полученной
линии в декартовой системе координат
и определите её тип.
4.5. 
Решение
Составим таблицу значений:
|
|
0 |
|
|
|
|
|
|
|
|
r |
5 |
≈4,07 |
≈2,66 |
≈1,75 |
≈1,25 |
≈0,97 |
≈0,82 |
≈0,74 |
|
|
|
|
|
|
|
|
|
|
|
≈0,71 |
≈0,74 |
≈0,82 |
≈0,97 |
≈1,25 |
≈1,75 |
≈2,66 |
≈4,07 |
5 |
Для вычерчивания линии
проведем радиусы-векторы, соответствующие
углам
 ,
взятым с интервалом
,
взятым с интервалом
 .
На каждом из этих радиусов-векторов
откладываем отрезки, равные значению
r при соответствующем
значении
.
На каждом из этих радиусов-векторов
откладываем отрезки, равные значению
r при соответствующем
значении
 из таблицы. Соединяя точки, являющиеся
концами этих отрезков, получаем график
данной линии:
из таблицы. Соединяя точки, являющиеся
концами этих отрезков, получаем график
данной линии:

Подставляя
 и
и
 в уравнение заданной линии, получим
в уравнение заданной линии, получим







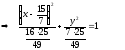

Полученное уравнение есть уравнение эллипса.
Задача 5
Найдите предел, не пользуясь правилом Лопиталя.
5.5. 
Решение

Задача 6
Найдите предел, не пользуясь правилом Лопиталя.
6.5. 
Решение

Задача 7
Найдите предел, не пользуясь правилом Лопиталя.
7.5. 
Решение

Задача 8
Найдите предел.
8.5. 
Решение



Задача 9
Заданы две функции f(x) и g(x). Сравните данные функции при помощи предела в окрестности точки х0=0 и установите, является ли в этой окрестности функция f(x) бесконечно малой по сравнению с g(x), бесконечно большой по сравнению с g(x), либо функции f(x) и g(x) имеют одинаковый порядок малости.
Указание: примените эквивалентные бесконечно малые функции.
9.5.

Решение
Сначала покажем, что данные функции являются бесконечно малыми:


Теперь найдем предел отношения данных функций:
 =
= 0
0
Так как пределы функций f(x) и g(x) в точке х0=0 равны нулю, можно сделать вывод о том, что функции f(x) и g(x) имеют одинаковый порядок малости.
Задача 10
Исследуйте на непрерывность функцию, заданную различными аналитическими выражениями на соответствующих интервалах. Если функция имеет точки разрыва, то установите их тип. Постройте схематический график заданной функции.
10.5. 
Решение
Исследуем на непрерывность точку x=-3
1)f(-3)=-(-3+3)=0 – функция определена в данной точке.
2) Найдём односторонние пределы:
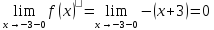

Односторонние
пределы конечны, но не равны между собой,
то
 -
точка разрыва первого рода.
-
точка разрыва первого рода.
Вычислим скачок разрыва как разность правого и левого пределов:
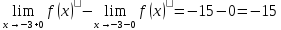 ,
то есть, график рванул на 15 единиц .
,
то есть, график рванул на 15 единиц .
Поскольку
в точке
 функция определена, то
функция определена, то
 -
точка разрыва функции. Исследуем характер
разрыва. Найдем односторонние пределы
функции в точке
-
точка разрыва функции. Исследуем характер
разрыва. Найдем односторонние пределы
функции в точке
 .
.

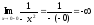
Т.к.
оба предела равны - ,
то
,
то
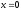 -
точка второго рода
-
точка второго рода