
Контрольная работа №3. Вариант 9
..docxВысшая математика.
Контрольная работа №3. Вариант 9.
Задание I.
Решить уравнение колебаний струны методом Фурье.
9.
 .
.
Решение.
Решение дифференциального уравнения свободных колебаний струны может быть представлено как сумма бесконечного ряда:
 ,
,
где
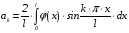 ,
,
 .
.
Находим
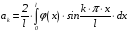 :
:
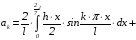
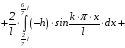
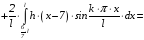
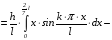
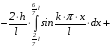
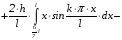
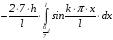 .
.
Интеграл
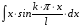 берем по частям. В результате получаем:
берем по частям. В результате получаем:
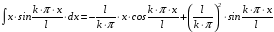 .
.
Отсюда следует:
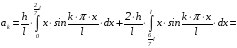
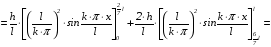
 .
.
Находим
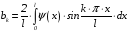 :
:
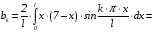
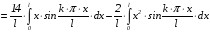 .
.
Интеграл
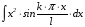 берем по частям. В результате получаем:
берем по частям. В результате получаем:

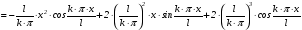 .
.
Вычисляем:
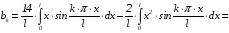
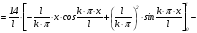
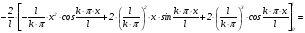
 .
.
Раскрывая скобки, получаем:
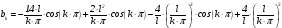 .
.
Окончательно:
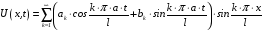 ,
где
,
где
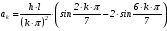 ,
,
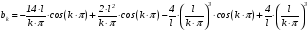 .
.
Задание II.
Для данной
функции комплексной переменной
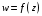 :
:
1) найти действительную и мнимую части,
2) указать
область дифференцируемости функции
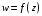 и найти ее производную,
и найти ее производную,
3) вычислить
интеграл по заданной кривой
 .
.
![]()
Решение.
1). Находим
действительную и мнимую части функции
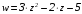 .
.
Подставляем
в функцию
 :
:
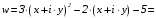
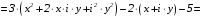
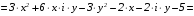
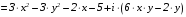 .
.
Для данной функции получили:
 – действительная часть;
– действительная часть;
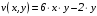 – мнимая часть.
– мнимая часть.
2). Определяем
область дифференцируемости функции
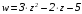 и находим ее производную.
и находим ее производную.
Для данной
функции проверяем условия Коши-Римана
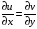 ,
,
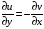 :
:
 ;
;
 ;
;
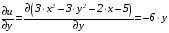 ;
;
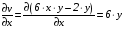 .
.
Условия
Коши-Римана выполняются при любых
значениях
 ,
,
 .
Следовательно, функция дифференцируема
в любой точке
.
Следовательно, функция дифференцируема
в любой точке
 комплексной плоскости
комплексной плоскости
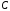 .
.
Находим производную функции:
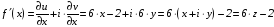 .
.
3). Вычисляем
интеграл функции
 по заданной кривой
по заданной кривой
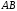 :
отрезок прямой,
:
отрезок прямой,
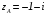 ,
,
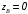 .
.
Функция
является аналитической на всей комплексной
плоскости
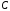 ,
поэтому воспользуемся формулой
Ньютона-Лейбница
,
поэтому воспользуемся формулой
Ньютона-Лейбница
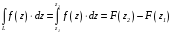 .
.
Получаем:
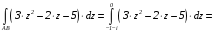
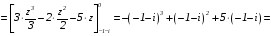
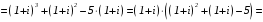

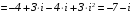 .
.
Задание III.
Средствами операционного исчисления решить задачу Коши.
![]()
Решение.
Пусть
 .
По теореме о дифференцировании оригинала
имеем:
.
По теореме о дифференцировании оригинала
имеем:
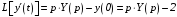 ;
;
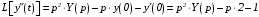 ;
;
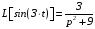 .
.
Получаем операторное уравнение:
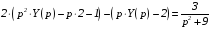 ;
;
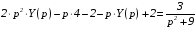 ;
;
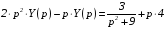 ;
;
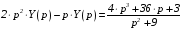 .
.
Находим изображение:
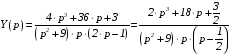 .
.
Методом неопределенных коэффициентов находим разложение полученного операторного решения уравнения в сумму простейших дробей:
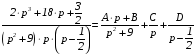 ;
;
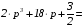

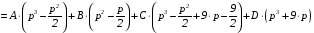 .
.
Получаем систему уравнений относительно неизвестных коэффициентов:
 ;
;
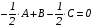 ;
;
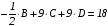 ;
;
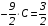 .
.
Решение системы можно получить по формулам Крамера:
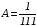 ;
;
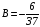 ;
;
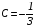 ;
;
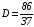 .
.
Получаем:
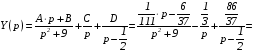
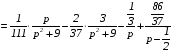 .
.
Отсюда имеем частное решение:

Задание IV.

Решение.
1). Для производственной практики на 30 студентов предоставлено 15 мест в Минске, 8 – в Гомеле и 7 – в Витебске. Какова вероятность того, что 2 студента попадут на практику в один город?
Решение.
Два любых места
практики можно выбрать из общего их
числа, равного 30, количеством способов,
вычисляемым как число сочетаний из
тридцати элементов по два:
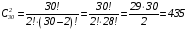 .
.
Пусть событие A
– двум определенным студентам достались
места для прохождения практики в Минске.
Так как мест в Минск предоставлено 15,
то количество исходов (комбинаций),
благоприятствующих событию A,
вычисляется как число сочетаний из 15
элементов по 2:
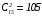 .
.
Пусть событие B
– двум определенным студентам достались
места для прохождения практики в Гомеле.
Так как мест в Гомель предоставлено 8,
то количество исходов (комбинаций),
благоприятствующих событию B,
вычисляется как число сочетаний из 8
элементов по 2:
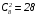 .
.
Пусть событие C
– двум определенным студентам достались
места для прохождения практики в
Витебске. Так как мест в Витебск
предоставлено 7, то количество исходов
(комбинаций), благоприятствующих событию
C,
вычисляется как число сочетаний из 7
элементов по 2:
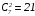 .
.
Следовательно, искомая вероятность:
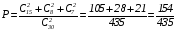 .
.
2). Вероятность наступления события в каждом из независимых испытаний равна 0,2. Найти вероятность того, что в 100 испытаниях событие произойдет не менее 20 раз и не более 30 раз.
При решении
задачи о вероятности того, что в n
испытаниях события А появилось не менее
m1 раз и не более m2
раза, используют интегральную функцию
Лапласа
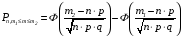 ,
где
,
где
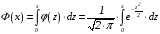 .
.
Формулу
Лапласа используют, если n – велико, а
р – значительное, то есть
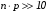 .
.
Имеем:
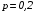 ;
;
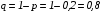 ;
;
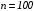 ;
;
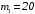 ;
;
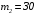 .
.
Условие
применения формулы Лапласа
 выполняется.
выполняется.
Вычисляем:
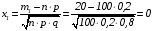 ;
;
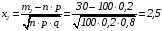 ;
;
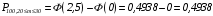 .
.
3). Найти числовые характеристики дискретной случайной величины, заданной законом распределения вероятностей
|
xi |
30 |
42 |
50 |
61 |
65 |
|
pi |
0,1 |
0,2 |
0,3 |
0,3 |
0,1 |
Расчетная таблица:
|
i |
xi |
pi |
xi·pi |
(xi)2 |
(xi)2·pi |
|
1 |
30 |
0,1 |
3,0 |
900 |
90 |
|
2 |
42 |
0,2 |
8,4 |
1764 |
352,8 |
|
3 |
50 |
0,3 |
15,0 |
2500 |
750 |
|
4 |
61 |
0,3 |
18,3 |
3721 |
1116,3 |
|
5 |
65 |
0,1 |
6,5 |
4225 |
422,5 |
|
|
|
M(X) = |
51,2 |
M(X2) = |
2731,6 |
Имеем:
количество
значений дискретной случайной величины
 ;
;
математическое
ожидание
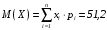 ;
;
дисперсия
 ;
;
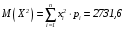 ;
;
 ;
;
среднее квадратическое отклонение
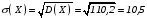 .
.
