Razbor_kriptov_-_chast_2

Данный материал содержит разбор всех лекций по криптографии. При необходимости – печатать рекомендуется в режиме «2 страницы на 1 листе».

Вторая часть криптографии – с чего же она начнется? Правильно, с новой темы.  А вместе с ней и с новых определений.

Периодические свойства последовательностей и преобразований

Обозначим Х_ = {x1, x2, …} – бесконечную последовательность над конечным множеством Х порядка k (или в виде символов |X| = k).

В данном случае фраза «над конечным множеством Х» означает, что элементы последовательности Х_ это элементы множества Х.

Перед тем, как двигаться дальше,сделаем одну важную оговорку. Дело в том, что обозначение Х_ на самом деле неправильное. Правильное обозначение выглядит вот так:

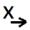(Х со стрелочкой внизу). Но это обозначение будет использоваться часто, а постоянно рисовать стрелочку слишком долго. Поэтому для простоты в нашем разборе будем обозначать его Х_. А вы будете обязательно иметь в виду, что это не нижнее подчеркивание, а стрелочка. Вроде все, теперь можно дальше.

А дальше – несколько определений о различных возможных подпоследоваельностях последовательности Х_, которую мы рассмотрели чуть выше.

Опр. Последовательность, состоящая из элементов xi1, xi2 и т.д. (обозн. {xi1, xi2…}), где i1…in

– упорядоченные по возрастанию числа, называется подпоследовательностью последовательности X_.

Опр. Последовательность вида {xθ, xθ+r, xθ+2r, …} называется (θ, r) – сечением последовательности Х_.

Если очень упрощенно, то θ здесь – начальный номер, а r – шаг. Подробности

будут несколько позже.

Опр. Конечная последовательность вида {xr, xr+1, …, xr+s-1} называется s-граммой последовательности Х_ (при s=2 называется биграммой, при s>2 –

мультиграммой). Другое обозначение – [r, r+s-1] – отрезок последовательности Х_. Упрощенно – сюда входит s элементов, начиная с r.

Обозн. Х*_ - класс всех бесконечных последовательностей над множеством Х.

Не очень очевидно, что это означает, поэтому поясним. Есть множество Х, есть

бесконечные последовательности над этим множеством: Х_ = {x1, x2…} и т.д. А

если взять все возможные бесконечные последовательности над Х, то получим как раз X*_.

Функции, определенные на последовательностях.

На последовательностях определены некоторые функции. Их незнание способно поставить под сомнение компетентность даже самого опытного криптографа. А уж

до взлома AES его точно не допустят. Чтобы не столкнуться с такой неприятностью, рекомендую начать их изучение прямо сейчас.

1.Перестановка членов последовательности g*(X_) = {xg(1), xg(2), …}

где g = (g(1), g(2), …) – перестановка членов натурального ряда.

Проще говоря, члены последовательности меняют местами.

2.Замена членов последовательности

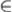f: X -> Y (на входе – элементы из Х, на выходе – из У, то есть xХ, а f(x) У)

f*(X_) = {f(x1), f(x2), …}

На выходе получаем уже новую последовательность из класса У (так как f

переводит элементы множества Х в элементы множества У).

3.Если Р – поле, то класс P_ (множество всех последовательностей над

полем Р, то есть элементы последовательности – это элементы из Р) образует векторное пространство относительно операции суммирования

(почленного) и умножения на элементы поля Р.

Базисом в данном случае является некоторая система векторов:

100…

010…

001…

Но она же бесконечная? Все верно. Так как последовательности рассматриваем бесконечные, то и размерность базиса бесконечна.

4.Сопряжение

Пусть имеются n таких последовательностей:

Xj = {xij}, где j=1..n

Сопряжением последовательностей X1_ … Xn_ называется последовательность X_ = {xi} над множеством Х = Х1 х Х2 х … х Хn.

Что значит ужасная надпись «над …»? В данном случае все просто – то, что каждый элемент последовательности – это вектор xi = (xi1 … xin). Первая

координата отвечает первой последовательности, вторая – второй и т.д.

Сопряжение обозначается: X_ = X1_ * X2_ * … * Xn_

А теперь сделаем ход конем умную штуку. Заметим, что каждый член последовательности Х_ - это вектор из n элементов. Если из последовательности Х_ у каждого ее элемента будем оставлять только j-ю

координату, то построим то, что называется j-я координатная подпоследовательность последовательности Х_. А теперь запишем это непонятным (хотя кому как) научным языком.

Опр. Последовательность (над Xj, так как все элементы – j-ые координаты) jx компонент всех элементов последовательности X_ называется j-й координатной подпоследовательностью последовательности X_ и обозначается X(i)_

5.Функция корреляции.

Пусть заданы 2 небесконечные последовательности Х_ и У_, в каждой из них содержится по t элементов над множеством E2.

Из нового, Е2 – это множество, состоящее из двух элементов: 0 и 1, то есть

E2 = (0,1).

Так вот, взаимной корреляцией (или функцией корреляции) последовательностей Х_ и У_ называется следующая функция:

Не пытайтесь пока понять эту функцию - просто примите ее такой, какая она

есть. Можете не сомневаться, в ближайшем будущем она вернется к вам птицей Феникс и заставит с собой разобраться. Пока лишь скажем, что она

используется для оценки близости Х_ и У_: X_ = {x0, …, xt-1}

Y_ = {y0, …, yt-1} E2 = {0, 1}

Замечание. CX_У_(d) = CY_X_(d)

Опр. Функцией автокорреляции (автокорреляцией) последовательности Х_

называется функция вида:

Она отличается от предыдущей лишь тем, что вместо «у» здесь – два раза

«х».

И вновь все, что мы можем сказать про эту функцию, это то, что она используется для оценки качеств Х_.

Замечание. CX_X_(d) = CX_(d)

Остается один вопрос – что такое d? Не так быстро. Его смысл мы узнаем

позже (или не узнаем). А пока мне лишь известны его область определения и значения, и я тороплюсь поделиться с вами этой информацией. Так вот: d определен в множестве вычетов по модулю t (проще говоря, от 0 до t-1), а

область значений – рациональные числа вида «что-то разделить на t». То есть

Опр. Последовательности Х_ и У_ над E2=(0,1) называются совершенно некоррелированными, если функция взаимной корреляции тождественно равна 0 при всех d из множества вычетов по модулю t (обозн. Et).

То есть CX_Y_(d) = 0 при любых d Et

Опр. Последовательности Х_ и У_ над Е2 называются максимально

некоррелированными, если функция взаимной корреляции находится в пределах от -1/t до 1/t. Вспомним формулу взаимной корреляции и получим прямо вот это:

Определяющие периодические свойства последовательностей

Последовательность Х_ называется периодической, если xi = xi+tay при всех I > µ, где tay – натуральное, µ натуральное или ноль.

То есть имеется совпадение на расстоянии tay.

Если µ наибольшее число, при котором xµ ≠ xµ+tay (то есть со следующего номера будут совпадения на расстоянии tay), то говорят, что в последовательности Х имеются совпадения на расстоянии tay, начиная с µ+1.

Опр. Наименьшее tay, при котором в Х_ имеются совпадения на расстоянии tay, называется длиной периода. Обозначается t(X_) – длина периода.

Ну действительно, если совпадение есть при tay=7, то оно будет и при tay=21 (ведь последовательность бесконечна), но длина периода – именно минимально возможное значение).

Опр. Длиной предпериода Х_ называется наименьшее натуральное число (или ноль) ν,

такое что в Х_ имеются совпадения на расстоянии tay, начиная с ν+1. Обозначается ν(Х_) – длина предпериода Х_.

Опр. Предпериодом последовательности Х_ называется отрезок [1, ν]

последовательности Х_.

Опр. Периодом последовательности Х_ называется отрезок [ν+1, ν+t] последовательности Х_.

Пример.

Утв.

1.Если в последовательности Х_ имеются совпадения на расстоянии tay начиная с

µ+1, то t|tay (tay делится на t) и ν=µ

2.Если последовательность У_ получена путем поэлементного применения функции f к последовательности Х:

Y_ = f*(X_) = {f(xi)}

где Х_ периодическая последовательность, то У_ также периодическая последовательность, причем длина предпериода У_ не больше длины предпериода Х_, и длина периода У_ делит длину периода X.

ν(У_) ≤ ν(Х_) t(Y_) | t(X_)

А если f – биекция, то: ν(У_) = ν(Х_)

t(Y_) = t(X_)

С биекцией действительно легко. Вот представьте, что есть бесконечная повторяющаяся последовательность: 12 304 304 304… Биективная функция такова, что все единицы переведет во что нибудь (например,

котят). Двойки – в слоников, тройки – в зайчиков. И все повторы останутся на местах. А вот не биективная может действовать не так очевидно, поэтому встречайте первое в этой части доказательство :)

Доказательство. Пункт первый.

Известно t и ν, а то что есть совпадения на расстоянии tay.

Понятно, что t ≤ tay, так как t – длина периода, а tay – лишь какое то совпадение. Если t = tay, то по определению совпадение на расстоянии t есть, начиная с наименьшего номера µ+1.

Отсюда ν = µ, то есть длина предпериода ν равна µ из условия.

Теперь рассмотрим случай, когда t ≠ tay.

И докажем, что (ν = µ) и (t | tay).

Для последнего пункта достаточно показать, что tay = kt. Предположим, что это не так, и он имеет вид tay = kt + r. где r – ненулевой остаток: 0 < r < t

k – натуральное Покажем, что r=0.

При i > max(ν, µ) – когда точно находимся на периоде – выполнены равенства:

xi+r = xi+r+tk = xi+tay = xi

Разберем подробно каждый переход:

1.xi+r = xi+r+tk – при переходе через несколько периодов t ничего не изменится – например: (12 304 304 304…) (12 304 304 304…)

2.xi+r+tk = xi+tay – чуть выше написано tay = kt + r

3.xi+tay = xi – по условию есть совпадения на расстоянии tay

А теперь – результат, посмотрите на начало и конец выражения:

xi+r = xi

Это означает, что получено совпадение на расстоянии r.

Что неверно, так как 0 < r < t, а t – длина периода (минимальное значение начала совпадений). Отсюда r = 0.

Теперь покажем, что ν = µ.

Пусть tay = tk.

Тогда хv+i = хv+i+t = хv+i+kt (прибавление 1 или нескольких периодов) При этом xv ≠ xv+t (иначе длина предпериода была бы не ν). Одновременно хv+i = хv+i+tay (чуть выше было tay = tk и хv+i = хv+i+t). Отсюда следует, что совпадения начнутся с ν+1 => ν=µ.

Другими словами то, что только что доказали. Если есть длина периода и длина предпериода, а также известно, что совпадения начинаются на некотором расстоянии начиная с ν, то это расстояние делится на длину последовательности, а все совпадения начнутся с того же ν.

Докажем теперь второй пункт утверждения.

Если xi = xi+t, то f(xi) = f(xi+t).

В последовательности У_ совпадения будут, начиная с µ+1 (равные элементы переходят в равные, поэтому длина периода не может вырасти)ю Но если f – не биективна, то совпадения могут начаться и раньше. А это значит, что длина предпериода может понизиться, но точно не увеличится. И все, что в такой ситуации можно сказать с уверенностью – что совпадения на расстоянии t останутся. Так как они были, и одинаковые элементы даже не биективная функция обработает одинаково. Отсюда t(Y_) | t(X_)

А вот если f – биективна, то длины периода и предпериода не изменятся: каждый элемент будет переведен в соответствующий ему элемент без потери уникальности.

Теорема.

Для последовательностей Х_ и У_ над конечной группой относительно операции сложения, построенных по правилу: yi = x1 + … + xi, верны следующие утверждения: А) Если Х_ периодическая последовательность с длиной предпериода ν и длиной периода t, то последовательность У_ также является периодической с длиной предпериода ν 1 и длиной периода t’, где t’|dt, где d – порядок элемента (yv+t yv) Пояснение: порядок элемента (обозн. ord) показывает, сколько раз элемент нужно сложить с самим собой, чтобы получить 0. В нашем случае d=ord(yv+t yv), причем (yv+t yv) – элемент из группы Х (вспомните, по какому правилу строим у. А можете не вспоминать – я его уже скопировал: yi = x1 + … + xi).

Б) Есть Х_ чисто периодическая последовательность (ν=0) с длиной периода t, то последовательность Х_ также чисто периодическая с длиной периода t’: t’|dt, где d=ord(yt). При этом выполняется: yjdt=0, где j=1,2,…

Доказательство. Пункт А.

yi = x1 + … + xi – по условию

Рассмотрим теперь это для расстояния dt:

yi+dt = x1 + … + xi+dt = yi + xi+1 + … + xi+dt =

= yi + (xi+1 + … + xi+t) + (xi+t+1 + … + xi+2t) + … + (xi+(d 1)t+1 + … + xi+dt).

Поясним каждый шаг:

1.yi+dt = x1 + … + xi+dt – рассматриваем для расстояния dt

2.x1 + … + xi+dt = yi + xi+1 + … + xi+dt – заменили x1 + … + xi на yi (т.к. yi = x1 + … + xi – по условию)

3.yi + xi+1 + … + xi+dt = yi + (xi+1 + … + xi+t) + (xi+t+1 + … + xi+2t) + … + (xi+(d 1)t+1 + … + xi+dt) –

разбили на слагаемые по t штук в каждом.

Тогда при i≥ ν будет по t элементов на период (i должно быть больше или равно длины предпериода, так как элементы i+1 … i+dt должны находиться на периоде). А раз так, то можно записать:

yi+dt = yi + d(xi+1 + … + xi+t) – полученные d блоков по t элементов (одинаковых: (xi+1 + … + xi+t) = (xi+t+1 + … + xi+2t) и т.д., т.к. там повторы).

yi+dt = yi + d(yi+t yi) – по определению yi (просто подставьте – и увидите, что все сойдется и получится выражение выше)

yi+dt = yi + d(yv+t – yv) – мы определили i≥ ν, но после выхода за пределы предпериода повторы будут всегда, не важно с какого элемента начать. Поэтому выбрали ν вместо i.

Чему равно d(yv+t – yv)? Давайте вычислять. Вспомним, что d здесь – это порядок элемента (yv+t – yv). А что такое порядок элемента? Это уже было в пояснении. Не ищите его, оно уже идет к Вам. Почти как Тайд.

Пояснение: порядок элемента (обозн. ord) показывает, сколько раз элемент нужно сложить с самим собой, чтобы получить 0. В нашем случае d=ord(yv+t yv), причем (yv+t yv) – элемент из группы Х (вспомните, по какому правилу строим у. А можете не вспоминать – я его уже скопировал: yi = x1 + … + xi).

Итак, d – количество раз, сколько нужно умножить элемент (yv+t yv) на себя, чтобы получить 0. Чему же тогда равно d*(yv+t – yv)? Правильно – нулю.

Получили: yi+dt = yi + [d(yv+t – yv) = 0]

Видим, что на расстоянии dt начались совпадения => длина периода последовательности У_ делит dt: t(Y_) | dt

Кроме того: yv = yv+dt => ν(Y_) = ν 1, то есть t(Y_) делит dt начиная с ν 1.

Покажем теперь, что совпадения начинаются именно с ν, а не с ν 1. Пусть в У_ есть совпадения, начиная с ν 1:

yv 1 = yv 1+dt

Перенесем все в одну часть:

yv 1+dt yv 1 = 0

Перейдем к «иксам»:

x1 + … + xv 1+dt – (x1 + … + xv 1) = xv + … + xv 1+dt = 0

Применим тот же способ, что чуть выше – разобьем по скобкам по t элементов:

xv – xv+dt + (xv+1 + … + xv+t) + (xv+t+1 + … + xv+2t) + … + (xv+(d 1)t+1 + … + xv+dt)

Всего получим d скобок по t элементов (видно по индексам у «икса»). (xv+1 + … + xv+t) = yv+t – yv

(xv+1 + … + xv+t) = (xv+t+1 + … + xv+2t) = … = (xv+(d 1)t+1 + … + xv+dt) = yv+t – yv

(везде равенство, т.к. там повторы) Получим, что все сводится к выражению: xv – xv+dt + d(yv+t – yv) = 0

Оно нам уже знакомо: d(yv+t – yv)=0, так как d=ord(yv+t – yv) – было чуть выше. Отсюда: xv = xv+dt

Но это невозможно, так как длина предпериода Х_ равна ν. Противоречие => совпадения начнутся с ν, а не ν 1.

Доказательство пункта Б.

Так как Х_ чисто периодическая, то если выбрать t элементов, окажемся на периоде, и если выбрать i+t элементов – тоже.

Ну а дальше – по знакомому из пункта А алгоритму:

yi+dt = yi + xi+1 + … + xi+dt = yi + (xi+1 + … + xi+t) + … + (xi+(d 1)t+1 + … + xi+dt)

Заметим, что (xi+1 + … + xi+t) = yt – сумма элементов на периоде (смещение i не важно)

(xi+1 + … + xi+t) = … = (xi+(d 1)t+1 + … + xi+dt) = yt

Итак:

yi+dt = yi + dyt, где d=ord(yt).

Так как d=ord(yt), получаем: dyt = 0 Отсюда: yi+dt = yi

Обнаруживаем совпадение на расстоянии dt, откуда делаем вывод: t(Y_) | dt

ν(Y_) = 0

Аналогичное доказательство и для Yjdt (j=1,2…):

Yjdt = x1 + … + xjdt = jd(x1 + … + xt) = jdyt = j(dyt) = 0, т.к. dyt=0 в связи с тем, что d=ord(yt).

Утв.

А. Последовательность Х_ над декартовым произведением Х1 х Х2 х … х Хn (т.е.

каждый элемент – вектор из n координат) называется непериодической тогда и только тогда, когда X(j) – периодическая (j=1…n), при этом: ν(X_) = max{ ν(X1_), …, ν(Xn_)} – чтобы везде попасть на период

t(X_) = НОК{ t(X1_), …, t(Xn_)}

Рассмотрим пример, показывающий это.

Х1_ = {123123123…} X2_ = {45454545…}

X1_ * X2 = {(1,4), (2,5), (3,4), (1,5), (2,4), (3,5), дальше повторяется…}

Б. Если X_ отличается от Х1_ лишь сдвигом на j 1 знак (например 12345 и 2345), то длина периода и длина предпериода:

t(X_) = t(X1_) ν(X_) = ν(X1_)

Ну действительно, если начать не с 1, а со второго – на период это никак не повлияет.

А при рассмотрении предпериода следует помнить, что по условию рассматриваем только такие последовательности, которые различаются лишь сдвигом на j 1 знак.

Следствие.

Если Х_ периодическая последовательность над декартовым произведением Х1

х Х2 х … х Хn (т.е. каждый элемент – вектор из n координат) и t(X_)= pm, где р – простое число, то t(X(i)_) = pmi – чтобы НОК всех таких t дал pm. max(m1…mn) = m

Пояснение: это нужно для удовлетворения условий пункта А: ν(X_) = max{ ν(X1_), …, ν(Xn_)}

t(X_) = НОК{ t(X1_), …, t(Xn_)}

Усложненные последовательности

Опр. Последовательность Y_={f(xi1,…,xin)} (пояснение: берем 1 элемент из Х1_, 1 элемент из Х2_ и т.д. и к этому набору применяем f), полученная из последовательности X_ = {(xi1, …, xin)} над декартовым произведением множеств Х1..Хn (т.е. каждый элемент – вектор из n координат) с помощью функции f:

X1 x X2 x … x Xn -> Y, называется усложненной по отношению к исходным последовательностям X1 … Xn, а f – функция усложнения

последовательностей X1…Xn.

Это интересно: если правильно подобрать f, то у X1 … Xn окажется

невысокая длина периода, а у У – огромная.

Свойства.

1.t(Y_) | НОК (t1 … tn), где: t1 = t(X1_)

tn = t(Xn_)

2.Если Х1_ и Х2_ - последовательности над аддитивной группой Х (то есть

группой относительно сложения) с длинами периодов t1 и t2, и f(x1x2) = x1 + x2, тогда t(Y) ≥ НОК(t1, t2) / НОД (t1, t2)

3.Если функция f(x1..xn) биективна по переменным с номерами: j1, …, jb,

где (j1…jb) {1..n}, то:

θ = НОК (t1, …, tn)

θji = НОК (t1, …, tji-1, tji+1, …, tn) – все кроме tji (t для всех, кроме xji)

4.Если f биективна по каждой переменной, и длины периодов t(X1_) … t(Xn_) попарно взаимно-просты, то длина периода последовательности У_ равна произведению: t(Y_) = t1 … tn

То есть можно взять последовательности с небольшим длинами

периода (попарно взаимно-простые), построить f и получить Y с огромной длиной периода).

Переходим ко второй лекции. Она связана с графами, и поэтому будет

достаточно легкой, как в прошлом семестре. А еще более приятный момент – в ней нет ни одного доказательства! Начнем.

Периодические свойства преобразований.

Пусть g – некоторое преобразование множества Х, и х – элемент из множества Х. Определим две следующих последовательности:

1. g_ = {gi}, i=0,1,… над П(Х) – моноидом всех преобразований множества Х.

Что такое П(Х), мы подробно разбирали в прошлом семестре. Сейчас лишь напомним, что это множество всех преобразований множества Х. Тогда слова «последовательность над П(Х)» означают, что все элементы последовательности – это преобразования из множества Х.

2.g_(x) = {gi(x)}, где i=0,1… над множеством Х (все элементы последовательности – это элементы множества Х).

То есть: g0(x) = x; g1(x) = g(x); g2(x) = g2(x) и т.д.