Razbor_kriptov_-_chast_2

Опр. Матрица Аg вида:

Называется сопровождающей матрицей линейного регистра сдвига. G{x1…xn} = (x1…xn)Ag.

Обозн. Линейный регистр сдвига длины n максимального периода будем обозначать как ЛРС max n.

Преимущества использования ЛРС max n:

1.Простота реализации и быстрота работы

2.Доказуемо высокая длина периода

Опр. Функции обратной связи ЛРС f = an 1xn + … + a1x2 + a0x1

однозначно соответствует многочлен F(λ) степени n над полем Р (т.е. коэффициенты являются элементами поля Р).

Вот так он выглядит: F(λ) = λn an 1 λn 1 … a1 λ a0 (« » можно заменить на и называется характеристическим многочленом этого ЛРС.

Пояснение по поводу знаков. На самом деле здесь стоят минусы, но на деле Вы будете встречать в основном . И в этом нетникакой ошибки: дело в том, что по модулю 2 таблицаистинности XOR соответствуетобычномувычитанию.

Утв. Критерий максимальности периода ЛРС.

Преобразование g ЛРС имеет максимальный период тогда и только тогда, когда F(λ) – примитивный многочлен.

Условия примитивности:

1.F(λ) – неприводим (нельзя разложить на множители, т.е. вынести за скобки)

2.F(λ) | λk^(n 1) 1

3.F(λ) не делит λd 1, где d|kn 1 и d ≠ kn 1.

Свойства.

1.Если F(λ) степени n неприводим над полем GF(2) и 2n 1 – простое число, то преобразование линейного регистра сдвига множества с характеристическим многочленом F(λ) имеет максимальный период.

Другими словами: если регистр сдвига – двоичный, 2n 1 – простое число и F(λ) – неприводим, то регистр имеет максимальный период.

2.Примитивный многочлен F(λ) над GF(2) содержит нечетное число членов.

Пояснение: если бы F(λ) содержал четное число членов, то имел бы корень 1. Это обычная математика и никакой криптографии – посмотрите на формулу F(λ)

и поймете, что, например, 4 операции XOR для единиц это 0.

Смотрите: F(λ) = λ3 λ2 λ 1. При λ=1 это будет: F(λ) = 1 1 1 1 = 0.

Вспомним теорему… не поверите… Безу. А она говорит, что если «а» является корнем многочлена, то многочлен делится на «х а». То есть F(λ) на что то будет делиться. Но она должна быть несокращаемой – поэтому четного количества членов быть не может.

3.Если F(λ) над GF(2) является примитивным, то и λnF( ) – также примитивный.

Пример.

F(λ) = λ27 λ19 1

F(1/ λ) = (1/ λ)27 (1/ λ)19 1 λ27F(1/ λ) = 1 λ8 λ27

Аффинные преобразования максимального периода.

Сейчас будет несколько определений. Пояснять там просто нечего – нужно принять их такими, какие они есть.

Опр. Пусть Р – поле, и есть ϕ: Pn > Pm (на входе – вектор длины n, на выходе – вектор длины m).

Тогда ϕ – линейная функция векторных пространств, если для любых x,y из Pn и для любых a,b из Р:

ϕ (ax+by) = aϕ(x) + bϕ(y)

ϕ*: Pn > Pm – аффинная функция векторных пространств, если ее можно представить в виде:

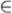ϕ*(x) = ϕ(x) + c, где xРn и сРm.

Опр. Биективное аффинное преобразование пространства Pn над полем Р порядка k, граф которого содержит цикл длины (kn 1), называется аффинным преобразованием максимального периода.

Опр. Аффинные преобразования h1 и h2 пространства Pn называются а параллельными, где а – ненулевой вектор пространства Pn, если h1(x) – h2(x)=a для любого xPn.

Замечание. А параллельные преобразования h1 и h2 либо оба биективные, либо оба не биективные (так как по предыдущему определению различаются только на константу).

Теорема. Пусть g – биективное линейное преобразование пространства Pn над полем Р, и h – это а параллельное ему аффинное преобразование. Тогда g и h либо оба являются, либо оба не являются преобразованиями максимального периода.

Пояснение: если хотим определить, имеет ли аффинное преобразование максимальный период, нужно посмотреть на соответствующее ему линейное преобразование. Они либо оба имеют максимальный период, либо ни одно.

А тем временем наш разбор продолжается. Сегодня Вы увидите в некотором смысле уникальную лекцию. В том смысле, что она на 90% состоит из определений. Около 5% потратим на небольшое рассуждение в самом начале, а еще 5% на комментарии и примеры к определениям. Поехали.

Конечные автоматы Мили

Опр. Автоматом (или автоматом Мили) называется система из 5 объектов: А = (X,S,Y,h,f), где:

1.X,S,Y – непустые множества

2.h : X x S > S (переводит элементы из декартового произведения X и S в элементы множества S. Дальше будет понятнее)

3.f : X x S > Y (аналогично предыдущему)

Обратите внимание: автомат и автомат Мили – это одно и то же! Не как производная и дифференциал, которые похожи, но различаются, и чтобы понять эти различия, нужно прочитать 5 томник по анализу.

Другими словами: автомат и автомат Мили – это действительно одно и то же, без звездочек и скрытых условий. Для закрепления предлагаю изучить тест (правильный ответ подчеркнут и выделен синим).

«Автомат» и «Автомат Мили»:

А. Это одно и то же

Б. Это похожие, но разные по смыслу автоматы В. То же, что п. Б, но «похожие по смыслу» Г. Это разные, но похожие автоматы Д. Это вообще не автоматы Е. Нет верного ответа

Множества X, S, Y называются соответственно входным, внутренним и выходным алфавитами.

Множество S также называют множеством состояний. Отображение h называется функцией переходов

Отображение f называется функцией выхода

Функционирование автомата

Автомат функционирует в дискретные компоненты времени (такты). В t м такте:

1.Автомат А находится в состоянии St S

2.Принимает на вход символ Xt X

3.Выдает выходной символ Yt Y

yt f xt, st

4. Переходит в новое внутреннее состояние St 1 h xt,st

Все этапы выполняются строго в данном порядке (1 > 2 > 3 > 4). Замечание.

Обозначим X*(Y*) – множество всех непустых слов в алфавите Х(У).

Обозначим пустое слово как Построим отображение:

h* : X* x S > S f* : X* x S > Y*

Итак, что же нужно знать, чтобы задать автомат? Оказывается, всего 2 пункта:

1.Начальное состояние

2.Что будет подано на вход

Этого достаточно, так как в таком случае мы сможем узнать новый выходной символ и новое внутреннее состояние. То есть сможем определить состояние автомата через несколько шагов.

Давайте подробнее рассмотрим несколько моментов.

Во первых: h*(, s) = s

Во вторых: f*(, s) =

В третьих, для любого х из Х и w X*: h* wx,s h x,h* w,s

Последний пункт требует небольшого пояснения. А именно, там написано, что сначала подали на вход w, при этом находясь в состоянии s. После этого перешли автомат перешел в новое состояние h* w,s .Затем подали навход символх, находясь ужевсостоянии h* w,s .Напомним, hзадает состояние, f – выходное слово. Теперь должно быть понятно, как распутывать подобную «рекурсию» речь о h x, h* w,s . Если так и не стало понятно, то отвечу прямо – изнутри.

Теорема.

Для произвольных слов наборов символов v,w из алфавита Х* и произвольного состояния автомата s S выполняются неравенства:

h* vw,s

h* w,h* v,s

f* vw,s f* v,s * f* w,h* v,s

Впрочем, тут написано то, что мынесколькострочек выше разбирали. Эта теорема лишь утверждает о том, что такое представление верно.

Вступление закончено, переходим к большому количеству определений 

Перед началом лишь скажу, что в них я не буду комментировать каждое отображение. Иначе просто будет неудобно читать. Поэтому запомните:

f : X X– означает «функция fпринимаетна вход элементиз Х ивозвращает элемент тоже из Х». Или нанаучном языке «функция fпереводит элементы множества Х в элементы множестваХ». Также можетобозначаться f П Х .

g: X x S Y– означает«функция принимает навход декартовопроизведение элементов из X и S,ивозвращаетэлементиз У». Или нанаучном языке «функция f переводит декартово произведение X и Sв элементы множества Х».

Также не забывайте, что в общем случае автомат задается 5 компонентами: (X,S,Y,h,f)

Опр. Преобразование hx :S S, определяемое как подфункция функциипереходов h x,s , соответствующая фиксированному значению х, называется частичной функцией переходов автомата А.

При слове x t x1,…,xt X*длиныt такой функцией называется преобразование: hx t s hxt… h2 hx1 s .

Физический смысл: определяет, в какой состояние перейдем из начального, если на вход подать слово длиныt.

Опр. АвтоматА называется регулярным перестановочным ,если все его частичные функции переходовбиективны.

Опр. Функция fx : S Y, определяемая какподфункция функции выходов f x,s , соответствующая фиксированному значению х, называется частичной функцией переходов автомата А.

Опр. Функция ft : Xt xS Y где Xt – множество слов длины tвалфавите Х , отображающая множество начальных состояний автомата А и входныхслов длиныt во множество значений t го знакавыходного слова, называется t й выходной функцией автомата А.

Пояснение:

ft x t ,s		f xt,hx t 1 s			fxt hx t 1 s .
Написано здесь вотчто:
1.	ft x	t ,s	– навход поступила последовательность x t , при этом автомат
2.	находился в состоянии s
	f xt,hx t 1		s к моменту поступления символаxt автомат находился в состоянии
3.	hx t 1	s	s	fxt hx t 1	s – просто обозначение
	f xt,hx t 1

Опр. АвтоматА называется внутренне автономным, если функция переходов не зависит отХ новое состояние определяется только его текущим состоянием .

Выходные функции внутренне автономного автомата определены выражением:

ft x t ,s

f xt,ht 1 s

fxt ht 1 s

Где: x t – словодлины t,s – начальноевнутреннее состояние автомата

ht 1 s – внутреннее состояние при поступлении t го символа

Обозначаются последовательные переходы внутренних состояний так:

s h s h2 s …

Опр. АвтоматА называется внешне автономным	или автоматом Мура , если
функциявыходов f не зависитот Х. то есть f: S	Y.

Выходные функции автомата Мура определены выражением:

ft x t ,s

f hx t 1 s

где: ft – t й знак выходного слова, s – начальное состояние, hx t 1 s – состояние автомата при поступлении символа t.

Заметьте, здесь было неважно, какой символ поступает наt шаге, зато очень важно внутреннее состояние: все зависит только от него! см. определение ещераз

Опр. Автомат А S,Y,h,f называется автономным, если он ивнутренне, и внешне автономный. Выходныефункции автономного автомата определены выражением:

ft s f ht 1 s .

Для лучшегопонимания лучше всего вспомнить предыдущие 2 определения:

1.Автомат А называется внутренне автономным, еслифункцияпереходовне зависит отХ новое состояние определяется только его текущим состоянием

2.Автомат А называется внешне автономным или автоматом Мура , еслифункция выходовfне зависит отХ

Данное же определениепредставляет собой объединение двух перечисленных. Заметьте, в полностью автономном автомате входное слововообще не важно, оно нигдене участвует!

Опр. Внутренне автономный автомат А X,S,Y,f с тождественной неизменной функцией переходов назовем автоматом с постоянной памятью.

Заметьте, в обозначении автомата отсутствует h: А X,S,Y,f .Все из за того, что она неизменна! Собственно, о чеми говорит определение.

Выходные функции автомата с постоянной памятью определены выражением:

ft x t ,s

f xt,s

fxt s .

Все s здесь одинаковы, нетникакихиндексов–ведь s неизменна!

Опр. АвтоматА X,Y,f реализующий отображение f : X Y,называется автоматом без памяти.

Другими словами: автомат просто реализует функцию f ибольше ничего полезного неделает.

Опр. Автомат А X,S,h называется автоматом без выходов

Действительно, f функция выхода и У выходной алфавит здесь отсутствуют.

СпособызаданияавтоматовМили.

Сначала рассмотрим способы какони есть,апотом приведем понятныйпример.

1. Табличныйξспособ,

Пусть Х

1

…, ξr

S

σ1, … , σn}

β1, …, βn

Y

Тогда функции:

hi

Xx S

S

fi

X x S

Y

в видеξ2

таблицы

Можно задатьξ1

…

ξr

ξ1

ξ2

…

ξr

σ1

h ξ2, σ2)

f ξ2, σ2)

σ2

…

σn

Левая часть таблицы задаетh: X xS S; правая f: Xx S Y.

Замечание. Число различных автоматов Мили А X,S,Y , где:

|X| r; |Y|	m; |S| n
равно:	mn rn
nrmmrm

Пояснение: nrm, так каквсего r*n ячеек, в каждой из них – n возможных состояний ведь |S| n . Для m – аналогично.

2.Задание с помощью автономного графа.

Автомат Мили А X,S,Y,h,f можно задать автоматным графом –

ориентированным графом ГА S,E – смножествомвершин S и множествомдуг

E.	σi, σj		ξ,		Еесть дуга в автомате А, если найдется хотябы 1 символ
Пара вершин
входного алфавита				l	такой что автомат переходит из состояния σi в
состояние σj при поступлении на вход ξl.
Обозн. h(ξl, σi) = σj, где l = 1…r
При этом дуга	σi, σj			помечается набором символов:		σ в состояние σ, если на
ξk1/βl1 … ξkt/βlt		,где автоматпереходитиз состояния				i	j

вход поступает любой из символов ξka (a=1..t).

На выходе будет:

h(ξka, ti) = σj f(ξka, ti) = βla

В автоматном графе автомата Мура помечаются и дуги, и вершины:

Дуга σi, σj помечается набором символов ξk1 … ξkt не нужнописать входных символов – от них ничего не зависит .

Вершина σi,помечается символом βli, который означает, что это выходной символ автомата, находящегося в состоянии σi,

Вот смотрите: βli = f (σi,)

Другими словами: выходные символы – вершины, входные – дуги.

Опр. Автомат А называется сильно связным, если автоматный граф автомата А сильно связен, то есть из каждого состояния можно перейти в любое другое при некоторой входной последовательности.

Опр. АвтоматА связен, если связен граф, полученный из графаавтомата А заменой дуг наребра то есть убрали стрелочки .

Рассмотрим долгожданный пример.									X,S,Y,h,f и задан в виде таблицы.
Пусть автомат А состоит из 5 объектов А
При этом X			Z3; S Z4; Y			Z3.
		0			1			2		0		1			2
0		1			0			0		1		0			1
1		1			1			0		0		1			1
2		1			1			2		0		1			1
3		3			2			0		1		0			1

Является ли такой автомат регулярным где все h – биективны ?

Нет, так как в каждом столбце не должно быть одинаковых чисел, и уже в первом это условие нарушается h0 – не биект. автомат не регулярен .

Построим граф автомата А. Ну и, раз идем вPaint, сделаем поясняющие подписи к таблице.

Навсякий случай поясним, каконбыл построен. Итак, задана таблица состояний и выходов.Нужно построить переходы дляначального состояния 0.

Пусть ему был подан на вход ноль. Тогда по таблице:

То есть при подаче на вход нулявнутреннее состояние окажется равным h 1, а возвращаемое значение f 1. Отображаем это прямо на графе:

На основе этого и былпостроен граф. Просто, не так ли?

Вернемся повыше, кужепостроенному графу, и ответим на2 вопроса.

Вопрос первый: является ли онсильно связным?

Ответ: нет, не является: должнобыть можно попасть из любой вершины влюбую, но из 0 в3 никак не попадем.

Вопрос второй: Является ли он связным? не сильно .

Ответ: да, является: если убрать стрелки заменить дуги на ребра , то любая вершина станетдостижимаиз любой другой.

Опр. Автоматы А и А’ называются однородными, если совпадают их входные алфавиты и выходныеалфавиты.

Обозн. Х Х’и Y Y’.

Опр. Однородные автоматы А и А’ называются согласованными, если:

Для любогоs SS’и длялюбогох изХ выполнено:

h’ x,s ,f’ x,s

h x,s , f x,s

То есть h’иh, f’и fсовпадают.

Замечание.

Если SS’ ø, то однородные автоматы А и А’ являются согласованными.

Насамом деле, это замечание – частный случай предыдущего определения: если пересечение есть, на него накладываются ограничения. А если пересечения нет, то нет и ограничений – и автоматы будут согласованными.

Сейчас будетопределение объединения автоматов, носначала отметим, что объединение определено толькодля согласованных автоматов.

Опр. Объединением согласованных автоматов Аи A’ обозначается АА’ называется автомат:

A’’	x, S	S’, Y, h’’, f’’		S		,	,если	S
Где h’’ x,s		,	,если		и f’’ x,s
		′ ,	,если	S′		′ ,	,если	S′

А вот тут без разницы, каким оператором действовать: h или h’. Почему? Потому что автоматы согласованы и в области пересечения работают одинаково h иh’ там совпадает .