
Юсупова Лекции
.pdfЛекция №1 Тема: Информация, сообщения, сигналы. (Часть 2)
1.Информация и сообщения
2.Структурная схема информационной системы
3.Классификация сигналов по дискретно-непрерывному признаку
Лекция №2 Тема: Вероятностные модели в задачах теории информации. (Часть 1)
1.Классификация сигналов с учетом неопределенности
2.Случайные события
3.Дискретная и непрерывная случайные величины
Тема: Измерение информации. (Часть 2)
1.Информация и теории информации
2.Структурные меры информации
3.Меры информации. Единицы измерения
4.Качество информации
Лекция №3,4 Тема: Информационная мера Шеннона
1.Информационная мера Хартли. Аддитивность информационной меры Хартли.
2.Информационная мера Шеннона. Связи с мерой Хартли.
3.Количество информации и энтропия.
4.Свойства энтропии дискретного источника сообщений
5.Количество информации и избыточность.
Лекция №5 Тема: Условная энтропия и взаимная информация. (Часть 1)
1.Условная энтропия
2.Взаимная информация
3.Пример с троичным каналом.
Тема: Каналы передачи информации. (Часть 2)
1.Структурная схема системы передачи информации (повторение);
2.Технические и информационные характеристики канала связи без помех;
3.Обобщенные характеристики сигналов и каналов;
Лекция №6 Тема: Каналы передачи информации с помехами
1.Вероятностные модели каналов передачи информации:
-двоичный канал
-троичный канал
2.Характеристики каналов передачи информации с помехами.
3.Современные технические средства передачи информации.
4.Методы повышения помехоустойчивости
Лекция №7 Тема: Результаты Шеннона и проблемы кодирования (Часть 1)
1.Теорема Шеннона для канала без помех;
2.Теорема Шеннона для канала с помехами;
3.Значение результатов Шеннона для задач передачи, хранения и поиска информации;
Тема: Эффективное кодирование (Часть 2)
1.Сжатие данных
2.Сжатие на основе статистических свойств данных.
2.1.Коды с переменной длиной кодового слова.
2.2.Вероятностная модель кодируемых сообщений.
2.3.Минимизация средней длины кодового слова.
Лекция №8 Тема: Эффективное кодирование (продолжение). (Часть 1)
1.Процедура Шеннона-Фано экономного кодирования.
2.Процедура Хафмана экономного кодирования.
3.Кодирование укрупненных сообщений.
4.Применение алгоритмов сжатия данных.
Тема: Помехоустойчивое кодирование. (Часть 2)
1.Основные принципы помехоустойчивого кодирования.
2.Количество кодовых комбинаций.
3.Помехоустойчивость кода.
4.Методы помехоустойчивого кодирования.
5.Классификация помехоустойчивых кодов.
6.Примеры систематических кодов.
Лекция №9 Тема: Частотное представление детерминированных сигналов
1.Периодические сигналы
2.Непериодические сигналы
3.Энергетическое толкование спектра
4.Примеры
Лекция №10 Тема: Дискретизация информации (Часть 1)
1.Классификация сигналов по дискретно-непрерывному признаку (повторение).
2.Квантование по уровню.
3.Дискретизация по времени. Методы дискретизации по времени.
Тема: Заключительные замечания по курсу (Часть 2)
1.Роль информационных процессов и систем.
2.Обзор основных тем дисциплин.
3.Значение основных результатов для науки и практики.
Лекция №1
Тема: Информация, сообщения, сигналы. (Часть 2)

1. Информация и сообщения
Теория информации – это наука о получении, преобразовании, накоплении, отображении и передаче информации.
В настоящее время существуют различные определения информации. Обычно под информацией в широком смысле понимают новые сведения об окружающем мире, который мы познаём в результате взаимодействия с ним.
С технической точки зрения, информация – это сведения, являющиеся объектом хранения, передачи и преобразования.
Информация – это прежде всего сведения, которые должны быть использованы. Нужно различать понятия «информация и «сообщение».
Под сообщением понимают информацию, выраженную в определенной форме и подлежащую передаче. Сообщение – это форма представления информации. Примерами сообщений являются: текст телеграммы, речь оратора, показания измерительного датчика, команды управления и т.д.
2. Структурная схема информационной системы
Структурная схема одной из характерных информационных систем в общем случае может быть
представлена как: |
|
|
|
|
|
|
|
|
|
|
Сообщение |
Сигнал |
|
Помехи |
|||||||
|
|
|
|
|
|
|
|
|
|
|
Источник |
|
|
Кодирующее |
|
|
|
Передатчик |
|
Линия |
|
информации |
|
|
устройство |
|
|
|
|
|
связи |
|
|
|
|
|
|
|
|||||
|
Информация |
|
|
Сигнал |
Сигнал-помеха |
|||||
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
Получател |
|
|
Декодирую- |
|
|
|
Решающее |
|
Прием- |
|
|
|
|
щее |
|
|
|
Канал связи |
|
ник |
|
ь |
|
|
|
|
|
устройство |
|
|
||
|
|
устройство |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Система состоит из отправителя информации, линии связи и получателя информации. Сообщение для передачи его в соответствующий адрес должно быть предварительно преобразовано в сигнал. Под сигналом понимается изменяющаяся физическая величина, отображающее сообщение. Сигнал – материальный переносчик сообщения, т.е. изменяющаяся физическая величина, обеспечивающая передачу информации по линии связи. Физическая среда, по которой происходит передача сигналов от передатчика к приемнику, называется линией связи.
Всовременной технике нашли применение электрические, электромагнитные, световые, механические, звуковые, ультразвуковые сигналы. Для передачи сообщений необходимо принять тот переносчик, который способен эффективно распределяться по используемой в системе линии связи (FE: по радиолинии эффективно распределяется только электромагнитные колебания высоких частот – от сотен кГц до дес. тысяч МГц).
Преобразование сообщений в сигналы, удобные для прохождения по линии связи, осуществляется передатчиком.
Впроцессе преобразования дискретных сообщений в сигнал происходит кодирование сообщения. В широком смысле кодированием называется преобразование сообщений в сигнал. В узком смысле кодирование – это отображение дискретных сообщений сигналами в виде определенных сочетаний символов. Устройство, осуществляющее кодирование называется кодером.
При передаче сигналы подвергаются воздействию помех. Под помехами подразумеваются любые мешающие внешние возмущения или воздействия (атмосферные помехи, влияние посторонних источников сигналов), а также искажения сигналов в самой аппаратуре (аппаратурные помехи), вызывающие случайное отклонение принятого сообщения (сигнала) от передаваемого.
На приемной стороне осуществляется обратная операция декодирования, т.е. восстановление по принятому сигналу переданного сообщения.
Решающее устройство, помещенное после приемника, осуществляет обработку принятого сигнала с целью наиболее полного извлечения из него информации.
Декодирующее устройство, (декодер)преобразует принятый сигнал к виду удобному для восприятия получателем.
3

Совокупность средств, предназначенных для передачи сигнала, называется каналом связи. Одна и та же линия связи может использоваться для передачи сигналов между многими источниками и приемниками, т.е. линия связи может обслуживать несколько каналов.
При синтезе систем передачи информации приходится решать две основные проблемы, связанные с передачей сообщений:
1)обеспечение помехоустойчивости передачи сообщений
2)обеспечение высокой эффективности передачи сообщений
Под помехоустойчивостью понимается способность информации противостоять вредному воздействию помех. При данных условиях, т.е. при заданной помехе, помехоустойчивость определяет верность передачи информации. Под верностью понимается мера соответствия принятого сообщения (сигнала) переданному сообщению (сигналу).
Под эффективностью системы передачи информации понимается способность системы обеспечивать передачу заданного количества информации наиболее экономичным способом. Эффективность характеризует способность системы обеспечить передачу данного количества информации с наименьшими затратами мощности сигнала, времени и полосы частот.
Теория информации устанавливает критерии оценки помехоустойчивости и эффективности информационных систем, а также указывает общие пути повышения помехоустойчивости и эффективности.
Повышение помехоустойчивости практически всегда сопровождается ухудшением эффективности и наоборот.
3. Классификация сигналов по дискретно-непрерывному признаку
Все сообщения по характеру изменяющиеся во времени можно разделить на непрерывные и дискретные. Непрерывные по времени сообщения отображаются непрерывной функцией времени. Дискретные по времени сообщения характеризуются тем, что поступают в определенные моменты времени и описываются дискретной функцией t.
Сообщения также можно разделить на непрерывные и дискретные по множеству. Непрерывные множеству сообщения характеризуются тем, что функция, их описывающая, может принимать непрерывное множество значений. Дискретные по множеству сообщения – это сообщения, которые могут быть описаны с помощью конечного набора чисел или дискретных значений некоторой функции.
Дискретности по множеству и времени не связаны друг с другом. Рассмотрим возможные типы сообщений подробнее.
Пусть сигнал описывается функцией X (t)
1)непрерывные по множеству и времени, или просто непрерывные; (рис. 1.2)
2)непрерывные по множеству и дискретные по времени; (рис. 1.3)
3)дискретные по множеству и непрерывные по времени; (рис. 1.4)
4)дискретные по множеству и времени, или просто дискретные;
3.1.
*1. Непрерывная функция непрерывного аргумента.
Значения, которые принимает функция x(t) и аргумент t, заполняют промежутки (xmin, xmax) и (-T,T) соответственно.
00
Непрерывная функция дискретного аргумента.
Значения функции x(t) определяю-тся лишь на дискретном множест-ве значений аргумента ti , 1, 2,....t T ,T
x(ti) может принимать любое значение на отрезке X min, X max
4
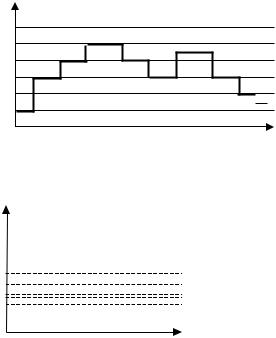
Дискретная функция непрерывного аргумента.
Значения, которые может принимать x(t), образуют дискретный ряд чисел x1,x2,x3,….,xk…, т.е. такой ряд, в котором каждому числу xk можно поставить в соответствие интервал (аk, bk), внутри которого других чисел данного ряда нет. Значение аргумента t может быть любым
T ,T .
2. Дискретная функция дискретного аргумента.
Значения, которые могут принимать x(t) и аргумент, образуют дискретные ряды чисел x1,x2,x3,….,xk… и –ti,…., -t2, -t1, t0, t1, t2, …, ti,…, заполняющие отрезки
xmin xmax , T ,T соответственно.
Лекция №2 Тема: ВЕРОЯТНОСТНЫЕ МОДЕЛИ В ЗАДАЧАХ
ТЕОРИИ ИНФОРМАЦИИ (Часть 1)
1. Классификация сигналов с учетом неопределенности.
5

2. Случайные события.
Событие - всякий факт, который в результате опыта может произойти или не произойти.
Вероятность события - это число, которое является мерой возможности реализации события. Вероятность
P(A) случайного события A заключена в пределах 0 P( A) 1.
Достоверное событие U такое, что P(U ) 1.
Невозможное событие V такое, что P(V ) 0.
Суммой или объединением событий называется событие A, которое происходит тогда и только
тогда, когда происходит, по крайней мере, одно из этих событий. Сумма обозначается
|
|
|
|
n |
A A A ... A |
|
A . |
||
1 |
2 |
n |
|
i |
|
|
|
|
i 1 |
Произведением или пересечением |
событий |
|
A1 , A2 ,..., An называется такое событие A, которое |
|
происходит тогда и только тогда, когда происходят события вместе. Произведение обозначается
n
A A1 A2 ... An Ai .
i 1
События A1 , A2 ,..., An образуют полную группу событий, если в результате опыта появляется хотя бы одно из них:
n
Ai U .
i 1
События A и B называются несовместными, если их совместное появление невозможно: AB V .
Два события называются противоположными, если они несовместны и образуют полную группу.
Событие, противоположное событию A, обозначается A .
6

A A U , AA V . Когда рассматриваемый опыт имеет N равновозможных исходов, которые несовместны и
составляют полную группу, вероятность события А можно рассчитать по формуле:
P( A) Nm ,
где m - число исходов, которые приводят к наступлению события A.
Частотой или статистической вероятностью P*(A) события A в данной серии испытаний называется отношение числа опытов n, в которых появилось событие, к общему числу N произведенных опытов:
P * ( A) |
n |
. |
|
N |
|
||
|
|
|
|
По теореме Бернулли при большом числе опытов частота сходится по вероятности к вероятности |
|||
события. |
|
|
|
Расчеты вероятности сложного события A через вероятности более простых событий |
A1 , A2 ,..., An |
||
базируются на использовании основных теорем теории вероятностей. |
|
||
Теорема сложения вероятностей. Вероятность суммы двух событий равна сумме вероятностей |
|||
этих событий минус вероятность их произведения: |
|
|
|
P(A B) P(A) P(B) P(AB). |
|
||
Теорема умножения вероятностей. Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого при условии, что первое имело место:
|
P(AB) P(A) P(A / B) P(B) P(A / B), |
где |
P(B / A) - условная вероятность события B, т.е. вероятность события B, вычисленная в |
предположении, что имело место событие A. |
|
|
Во многих ситуациях событие A может появиться лишь как случайное следствие одного из |
несовместных событий |
Bj , j 1,n, |
образующих полную группу. В этих случаях безусловная вероятность |
P(A) события A при известных вероятностях |
P(Bj ) и P( A / Bj ), j 1,n |
определяется по формуле полной |
вероятности: |
|
|
n |
n |
|
P( A) P( ABj ) P(Bj ) P( A / Bj ). |
||
i 1 |
i 1 |
|
При этих же данных можно найти значения вероятностей событий Bj , если предположить, что событие A уже произошло. Задачи такого типа решаются с помощью формулы Байеса:
P(Bj / A) P(Bj ) P( A / Bj ) / P( A),
Рассмотрим несколько примеров.
n |
|
P( A) P(Bj ) P( A / Bj |
). |
i 1 |
|
7
Пример 1. В последовательности из N двоичных символов имеется M единиц. При передаче
данной последовательности сохраняется n символов, остальные теряются. Какова вероятность того, что среди них будет не более m единиц?
Решение. Пусть A - событие, состоящее в том, что среди двоичных символов будет не более m
единиц. Событие A произойдет тогда, когда среди n двоичных символов не будет ни одной единицы
(событие |
A0 ) или одна единица (событие |
A1 ), |
или две (событие A2 ), |
. . ., или окажется m единиц |
||||||||||||||||||
(событие |
Am ), т.е. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
A A A A ... A |
|
|
|
|
A . |
|
|
|
|
|
||||||||||
|
|
|
0 |
1 |
2 |
|
|
|
m |
|
|
|
k |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
Вероятность P( Ak ) события Ak можно рассчитать следующим образом. Общее число возможных |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
. Благоприятствующими событию Ak |
|||||
выборов n символов из N равно числу сочетаний из N по n, т.е. |
CN |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
K |
|
являются случаи, когда из общего числа M единиц сохранено ровно K, что возможно в |
CM случаях. На |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n K |
|
каждый |
из этих случаев в |
сохраненной последовательности |
|
символов |
может быть |
CN M различных |
||||||||||||||||
комбинаций ( n K ) нулей. |
Общее число случаев, благоприятствующих событию Ak , |
K |
n K |
|||||||||||||||||||
равно CM CN n . |
||||||||||||||||||||||
Поэтому |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P( A ) C |
K |
C |
n K |
/ C |
n |
. |
|
|
|
|
|
|
|||||||
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
K |
|
|
N M |
|
|
|
N |
|
|
|
|
|
|
|
||||
По теореме сложения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P( A) |
|
mP( A ) |
|
C |
K |
|
C |
n K |
/ C |
n |
. |
|
|
|
||||||
|
|
M |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
k |
|
|
|
|
N M |
N |
|
|
|
|
||||||||
|
|
|
K 0 |
|
|
|
|
K 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 2. По каналу связи с помехами передается одна из двух команд управления управления в
виде кодовых комбинаций 11111 и 00000, вероятности передачи этих команд равны соответственно 0,7 и 0,3. Вероятность правильного приема каждого из символов 0 и 1 равна 0,6. Символы искажаются помехами независимо друг от друга. На выходе канала имеем кодовую комбинацию 10110. Оценить,
какая команда была передана.
Решение. Пусть A - событие, состоящее в приеме комбинации 10110. Это событие может
произойти только в совокупности с |
одним из событий: |
B1 - передавалась команда 11111, B2 - |
|
передавалась команда 00000. При этом |
P(B ) 0,7, |
P(B ) |
0,3. |
|
1 |
2 |
|
Условная вероятность приема комбинации 10110 при условии, что передавалась команда 11111 |
|||
равна |
|
|
|
P( A / B ) P(1 / 1) P(0 / 1) P(1 / 1) P(1 / 1) P(0 / 1), |
|||
1 |
|
|
|
P(1 / 1) 0,6, P(0 / 1) 1 P(1 / 1) 0,4,
3 |
0,4 |
2 |
0,035. |
P( A / B ) 0,6 |
|
||
1 |
|
|
|
Аналогично
P( A / B ) 0,4 |
3 |
2 |
0,023. |
|
0,6 |
||
2 |
|
|
|
По формуле Байеса
P( B1 / A) |
P( B1 ) P( A / B1 ) |
0,78, |
P( B2 / A) 0,22. |
n |
|||
|
P( Bn ) P( A / BK ) |
|
|
K 1
8
Сравнивая найденные результаты, заключаем, что более вероятна передача команды 11111.
3. Дискретная и непрерывная случайные величины
3.1.Модель дискретной случайной величины.
Случайной величиной называется такая переменная величина, которая в результате опыта может
принимать то или иное заранее неизвестное значение |
, из известного множества значений |
X . |
Различают два основных типа случайных величин: дискретные и непрерывные.
Дискретная случайная величина может принимать конечное или бесконечное множество значений {x1} , которые можно пронумеровать i 1,2,...,n.
понимается соотношение, устанавливающее зависимость между возможными значениями дискретной
n |
|
случайной величины и их вероятностями P(xi ) pi , при этом pi |
1. |
i 1 |
|
Закон распределения случайной величины можно задать |
в различных формах: табличной, |
графической, аналитической. Во многих ситуациях невозможно определить закон распределения случайной величины, часто в этом нет необходимости. В таких ситуациях рассматривают отдельные параметры (числовые характеристики) этого закона. Наиболее важными числовыми характеристиками случайной величины с множеством значений X {x1 ,x2 ,...,xn} и законом распределения вероятностей
P {p |
, p |
,..., p } |
1 |
2 |
n |
являются:
m
2
|
|
n |
|
|
|
|
|
|
|
|
|
m[ ] xi pi - математическое ожидание; |
|||||||||||
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
2 |
m[ |
2 |
] |
|
|
2 |
pi |
|
|
|
|
m |
|
xi |
- средний квадрат; |
||||||||
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
m[( m ) |
2 |
] |
(xi |
m ) |
2 |
pi - дисперсия. |
|||||
|
|
||||||||||
|
|
|
|
|
|
i 1 |
|
|
|
|
|
Рассмотрим несколько примеров.
|
Пример 1. По двоичному каналу связи с помехами передаются две цифры 1 и 0 с вероятностями |
|
p1 |
p2 0,5. |
Вероятность перехода единицы в единицу и нуля в нуль соответственно равны p 1 / 1 p |
, p(0 / 0) q. |
Определить закон распределения вероятностей случайной величины - однозначного |
|
числа, получаемого на приемной стороне.
Решение. X {0,1}. Нуль ( 0) на приемной стороне может быть получен в двух случаях:
при передаче нуля или при передаче единицы, следовательно, по формуле полной вероятности
P (0) P(0,0) P(1,0) P(0) P(0 / 0) P(1) P(0 / 1),
P(0 / 1) 1 P(1/ 1).
Поэтому P (0) 0,5q 0,5(1 p) 0,5(1 q p).
Аналогично P (1) P(0,1) P(11,) 0,5(1 q p).
Распределение вероятностей представлено в табл. 1.
9

x |
i |
|
pi
0
0,5(10p q)
Табл. 1.
1
0,5(1 p q)
Пример 2. Производится прием символов 0 и 1 до первого появления символа 1. Вероятность
появления 1 при |
приеме |
|
P(1) 0,4 . |
|
Принимается |
не |
более четырех символов. Вычислить |
|||
математическое ожидание m |
|
|
2 |
|
и среднеквадратическое отклонение |
|
||||
, дисперсию |
|
|
|
величины числа |
||||||
принятых символов. |
|
|
|
|
|
|
|
|
|
|
Решение. Распределение вероятностей можно рассчитать следующим образом: |
|
|||||||||
P[ 1] p |
p(1) 0,4; |
|
|
|
|
|
|
|
||
1 |
|
|
|
|
|
|
|
|
|
|
P[ 2] p |
p(0) p(1) (1 0,4) 0,4 0,24; |
|
|
|||||||
2 |
|
|
|
|
|
|
|
|
|
|
P[ 3] p |
p(0) p(0) p(1) |
0,8 |
2 |
0,4 0,144; |
|
|
||||
|
|
|
||||||||
3 |
|
|
|
|
|
|
|
|
|
|
P[ 4] p |
p(0) |
3 |
p(1) p(0) |
4 |
|
|
3 |
4 |
0,216. |
|
|
|
0,6 0,4 |
0,6 |
|
||||||
4 |
|
|
|
|
|
|
|
|
|
|
По определению математического ожидания имеем:
|
|
n |
|
m |
|
x p |
|
|
|
i |
i |
|
|
i 1 |
|
1 0,4 2 0,24 3 0,144 4 0,216
2,2
,
для дисперсии получаем:
|
|
|
n |
|
|
|
|
|
|
|
2 |
|
|
(x m ) |
2 |
p |
1,38; |
||
|
|
||||||||
|
|
|
i |
|
|
i |
|
||
|
|
|
i 1 |
|
|
1,17. |
|
||
|
|
2 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.2. Модель непрерывной случайной величины.
Универсальной характеристикой, одинаково пригодной для дискретных и для непрерывных одномерных
случайных величин, является функция распределения вероятностей |
F(x) (интегральная функция |
||
распределения), определяющая вероятность P того, что случайная величина X примет значение меньше |
|||
некоторого некоторого числа x : |
|
|
|
|
F(x) P( X x). |
|
|
Функция распределения обладает следующими свойствами: |
|
|
|
1. |
F( ) lim F(x) 0. |
|
|
|
x |
|
|
2. |
F( ) lim F(x) 1. |
|
|
|
x |
|
|
3. |
F(x) неубывающая функция, т.е. F ( x2 ) F ( x1 ) при x2 |
x1 . |
|
4. |
P(x1 X x2 ) F( x2 ) F(x1 ) . |
|
|
Функция распределения дискретной случайной величины представляет собой ступенчатую
функцию со скачками в точках x1 , x2 , ...
10
